自动搬运

查看原文

来自洛谷，原作者为

	Gu_Pigeon ​​​​​​​​​​​​​​​​​​​​

搬运于2025-08-24 21:31:43，当前版本为作者最后更新于2019-08-12 16:41:50，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

题解 兼 学习笔记

明显的一道带修莫队，于是去认真学习了一番，对莫队也有了一些新的理解。

这一切的一切，都要从最初的问题说起……

“很久很久以前，有一个序列……”

当序列上只有一个询问，例如，求区间颜色种数时，我们可以$O(n)$时间内解决这一个孤零零的问题。

但是，当询问数变成了m，这题就变成了HH的项链，我们不能总是一个一个求，明显TLE。

此时，我们想到，由上一次查询的结果，通过对左右端点的移动，我们就可以得出新的解。

从[l,r]到[l+1,r]、[l-1,r]、[l,r+1]、[l,r-1]的转移都是$O(1)$的，所以……等等!

要是我们把中括号改成小括号……

(l,r)->(l-1,r)(l+1,r)(l,r-1)(l,r+1)

这不就是平面直角坐标系吗！

一不做二不休，把它画出来：

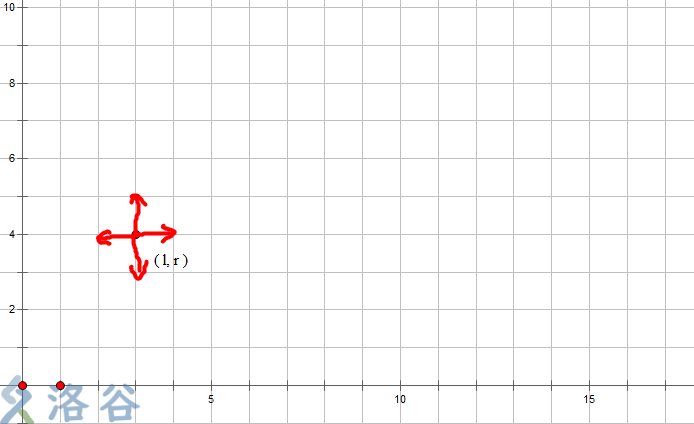
（图丑轻喷…）

图中四个箭头的移动都是可以$O(1)$完成的，那么两点之间的曼哈顿距离就是从一个状态到另一个状态所需要的最小挪动

（不了解曼哈顿距离的同学戳上面加粗字体）

那么对于所有的查询，最快的办法就是在坐标系上找到曼哈顿最小生成树

（其实没有必要会这个因为太麻烦了）

你也许会说：“我不会啊！”

这完全没有关系，因为

我也不会

但是我们并没有必要得到最佳答案，能卡过去就够了。

于是我们采用分块的想法，将其分成(n/sz)个长度为sz的块，在每一个块中按照右端点从小到大来移动

就像这样：

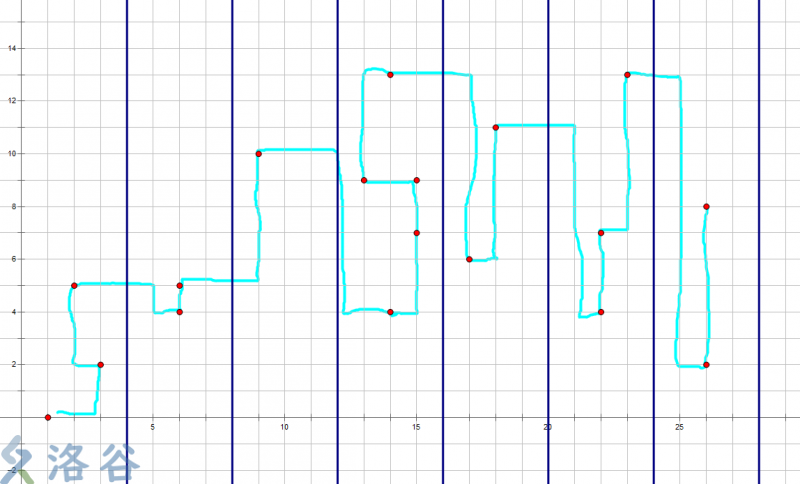
至少这样不会被卡掉……

至于块的大小？$\sqrt n$呗。

（实际上严谨的说，应该是$\dfrac {n}{\sqrt {m}}$，具体为啥有兴趣的同学可以研究一下，一般来说块的大小$\sqrt n$足矣，因此不在此介绍）

那么我们就讲好了本题……的前置部分……

好了！现在我们在这里加入了修改，“我该怎么办呢qwq”

可以这么认为，序列的值是随着时间而变化的

那我们就在坐标系上再加上一个时间维度，用(l,r,t)来表示一个查询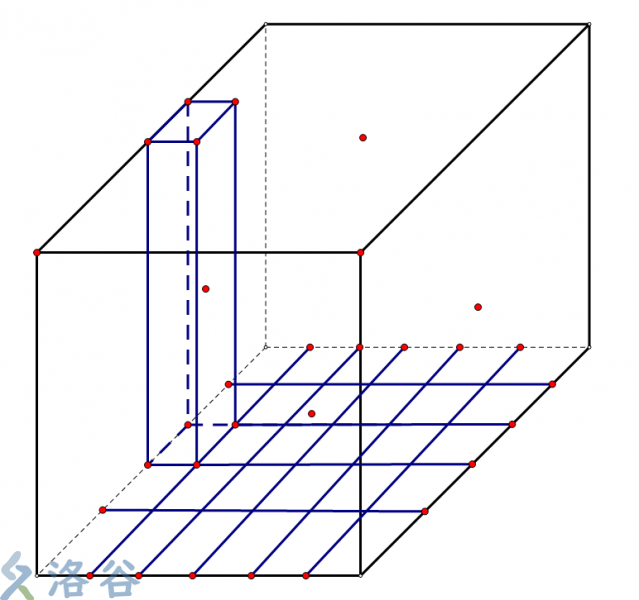

↑大概就是这样

很明显，我们需要分别按照l与r分块，在同一块内的询问按照t从小到大完成。块的大小就是${\sqrt [3] {n^{2}}}=n^{0.6666...}$

（至于为什么还是看别的题解吧，窝太菜廖）

所以总的来说，只需要在原有的普通莫队上在加一个时间维度就可以了

$Code\ Below$

#include<bits/stdc++.h>
using namespace std;
#define N 233333
#define M 1111111

int sum, cnt[M], a[N], ans[N], cntq = 0, cntr = 0, n, m, sz;

struct ques
{
	int l, r, t, id;
} qq[N], qr[N];//两个数组分解记录每一个询问以及修改的状态

inline void add(int x)
{
	sum += !cnt[x]++;
}

inline void del(int x)
{
	sum -= !--cnt[x];
}

//add与del是普通莫队原有操作

inline void upd(int x, int t)//upd是对于时间上的变化所造成变化的维护
{
	if (qq[x].l <= qr[t].l && qr[t].l <= qq[x].r)
	{
		del(a[qr[t].l]);
		add(qr[t].r);
	} //如果这个修改的值在[l,r]区间内，则其变化将对答案造成影响
	swap(a[qr[t].l], qr[t].r);//因为修改后的下一次操作一定相反(即修改该位置->还原该位置->修改该位置...如此循环)，所以只需交换即可，而不需要写两个函数
}

bool cmp (const ques &a, const ques &b)
{
	return a.l / sz == b.l / sz ? a.r / sz == b.r / sz ? a.t < b.t : a.r < b.r : a.l < b.l;
}//魔改版cmp，需要判断t的大小

int main()
{
	cin >> n >> m; sz = pow(n, 0.666);//设置块的大小
	for (int i = 1; i <= n; i++) scanf("%d", a + i);
	for (int i = 1; i <= m; i++)
	{
		char op[5];
		int l, r;
		scanf("%s%d%d", op, &l, &r);
		if (op[0] == 'Q') ++cntq, qq[cntq].id = cntq, qq[cntq].l = l, qq[cntq].r = r, qq[cntq].t = cntr;//询问的时间即为该询问以前已经执行了多少次修改操作
		else qr[++cntr].l = l, qr[cntr].r = r;
	}
	sort(qq + 1, qq + cntq + 1, cmp);
	int lcur = 1, rcur = 0, tcur = 0;
	for (int i = 1; i <= cntq; i++)
	{
		while (lcur > qq[i].l) add(a[--lcur]);
		while (lcur < qq[i].l) del(a[lcur++]);
		while (rcur > qq[i].r) del(a[rcur--]);
		while (rcur < qq[i].r) add(a[++rcur]);
		while (tcur < qq[i].t) upd(i, ++tcur);
		while (tcur > qq[i].t) upd(i, tcur--);//增加t轴上的移动
		ans[qq[i].id] = sum;//得到最终答案
	}
	for (int i = 1; i <= cntq; i++) printf("%d\n", ans[i]);
	return 0;//结束&AC!
}

求赞QwQ

顺便无耻地打个AD：$My Blog$