自动搬运

查看原文

来自洛谷，原作者为

	Social_Zhao 悲しくって 泣いてるわけじゃあない

搬运于2025-08-24 21:31:42，当前版本为作者最后更新于2019-07-07 10:41:17，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

Part 0 前言

这是你没有见过的船新解法。

请自动忽略算法标签。

---

Part 1 考虑正解——二分+bfs

我们在题面中看到了最大值最小 这五个字。

很容易就想到了二分答案。

然鹅我的dfs挂了，所以我就写了bfs，阿掉了。

本来就是很裸的做法，限于篇幅，这里就无需赘述了。

#include<bits/stdc++.h>
using namespace std;

int get()
{
	int x = 0, f = 1; char c = getchar();
	while(!isdigit(c)) { if(c == '-') f = -1; c = getchar(); }
	while(isdigit(c)) { x = x * 10 + c - '0'; c = getchar(); }
	return x * f;
}

const int MaxN = 1005;
const int inf = 0x3f3f3f3f;
const int dx[5] = {0, 1, 0, -1, 0};
const int dy[5] = {0, 0, 1, 0, -1};
int p[MaxN][MaxN], vis[MaxN][MaxN];
int n, m;
int l = inf, r = -inf, mid, ans, f; 

bool bfs(int x, int y, int maxn) //判断mid是否可行的bfs
{
	queue<pair<int, int> > q;
	q.push(make_pair(x, y)); //STL里的pair，个人认为要方便一些
	vis[x][y] = 1; 
	while(q.size()) { //以下就是bfs板子
		int xx = q.front().first; 
		int yy = q.front().second;
		q.pop();
		for(int i = 1; i <= 4; i++) {
			int nx = xx + dx[i];
			int ny = yy + dy[i];
			if(nx < 1 || nx > n || yy < 1 || yy > m || vis[nx][ny] || p[nx][ny] > maxn)
				continue; //不可行（越界、已访问、伤害过大）的直接跳过
			vis[nx][ny] = 1;
			if(nx == n) return 1; //到了，返回1
			else q.push(make_pair(nx, ny));
		}
	}
	return 0; //没有搜到，返回0
}

int main()
{
	n = get(), m = get();
	for(int i = 1; i <= n; i++) {
		for(int j = 1; j <= m; j++) {
			p[i][j] = get();
			r = max(r, p[i][j]);
			l = min(l, p[i][j]);
		}
	}
	while(l <= r) { //二分答案模板
		mid = (l + r) >> 1;
		f = 0;
		memset(vis, 0, sizeof(vis)); //重置数组
		if(bfs(1, 1, mid)) r = mid - 1, ans = mid; //如果这个mid可行，说明可能还能再小，于是更新答案 + 缩小范围
		else l = mid + 1; //mid此不可行，说明不可能再小，也缩小范围，不更新答案
	}
	printf("%d", ans);
	return 0;
}

Part 2 新解法

二分这种算法对题中的p[i][j]的依赖较严重。如果加强数据，改到$10^9$怎么办呢？

这样就需要一个靠n、m吃饭的算法了

在看这个解法前，您需要一些图论知识

让我们把样例画成一张图：（暂不带权）

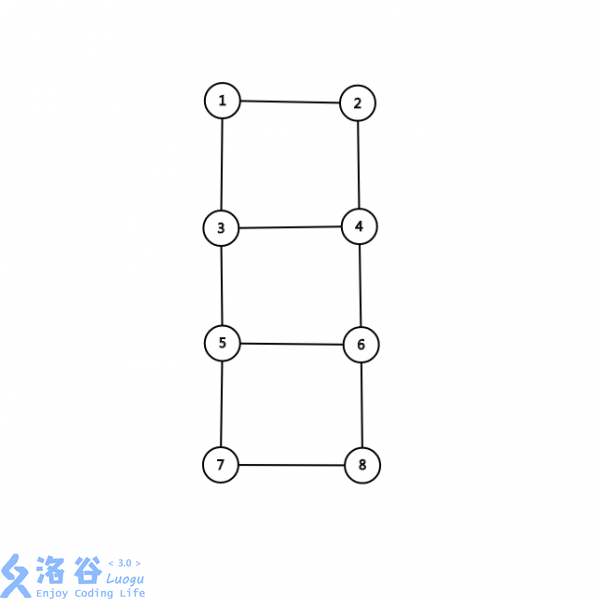
这个图得到的方法：

设点号为k，这个点是x行y列。

则有：$k=(x-1) \times m + y$

我们的任务是从第一行到第四行，求出经过的最大点权最小（有一点绕）

首先我们需要把点权转成边权：

仔细地钻研这句话：

最大点权最小

解读：

• 根据最大，我们可以想到如果我们要点转边，两点之间的边权应为两端点的点权最大值。

  • 根据这个边转点的原理，可以得到这一张图：

  

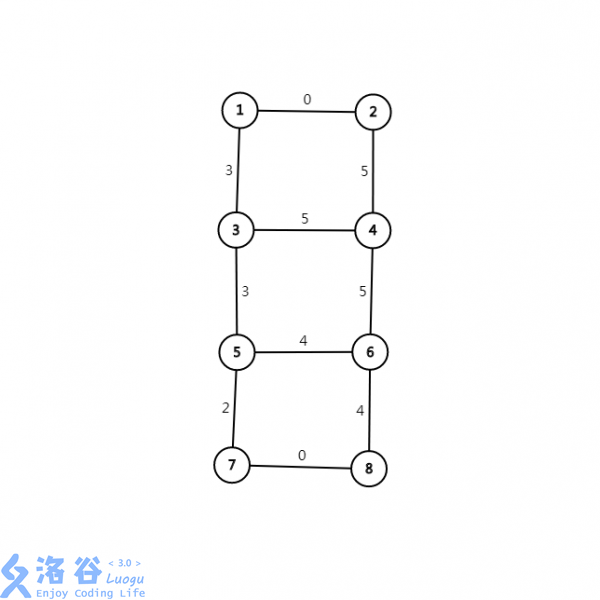
• 根据最小，得出：我们需要选择一些边来使第一行和最后一行连通，这些边的权尽量小

现在我的思路就显而易见了：MST（最小生成树）

但是又不是裸的最小生成树。我们不需要选择n-1条边，只需要使首尾两行连通。

所以我们选择Kruskal算法，用并查集维护：

按照题面，第一行和最后一行的边权都是0，中间又不可能出现负权，所以我们的算法会首先选出这些边，因此可以认为这些点从一开始就是连通的，并且可以认为，将这两行都连通，就等价于将分别位于这两行上的任意两点连通。为了简便，我们将第一个点和第八个点连通。如图：红边表示已选边，黑边未选边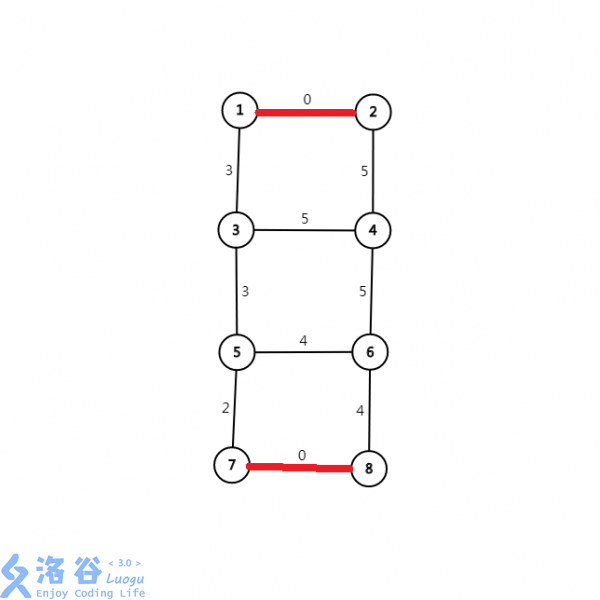

现在按照生成树算法，开始选其他边

第一步，选择目前最小的未选边——在5和7之间，边权为2的边：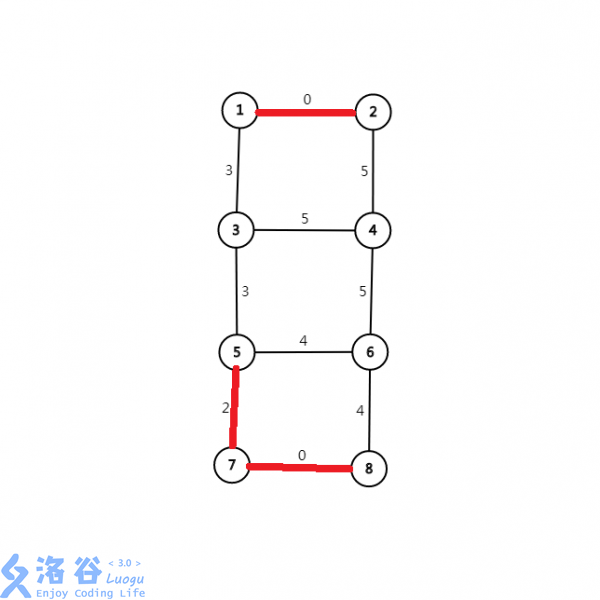

第二步、第三步，选出目前边权最小的边，分别是——在3和5之间，边权为3的边、在1到3之间，边权为3的边（节约篇幅，一并画出）：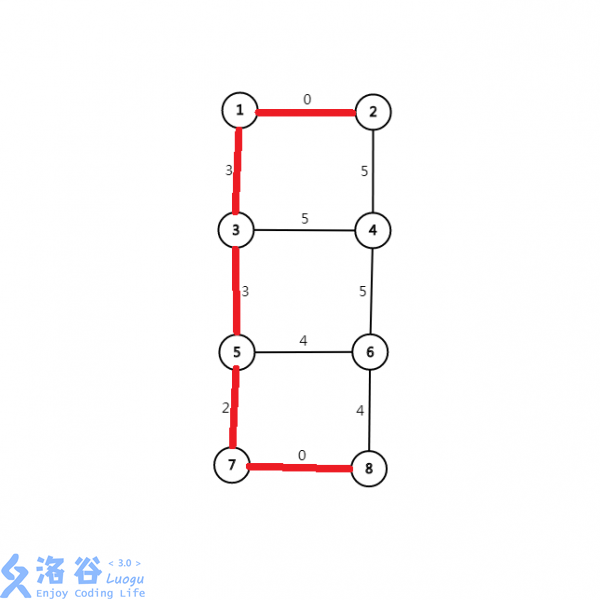

这时候，我们愉快地发现，1号和8号已经连通了。算法结束，答案为3。

上代码：

#include<bits/stdc++.h>
using namespace std;

int get()
{
	int x = 0, f = 1; char c = getchar();
	while(!isdigit(c)) { if(c == '-') f = -1; c = getchar(); }
	while(isdigit(c)) { x = x * 10 + c - '0'; c = getchar(); }
	return x * f;
}

const int MaxN = 1005;
const int inf = 0x3f3f3f3f;
int p[MaxN][MaxN];
int n, m, maxn = -inf;
struct Edge {
	int u, v, w;
} edge[10000005];
int k = 0;
int fa[10000005];

int MAP(int x, int y) { return (x - 1) * m + y; } //此函数用于求（x，y）在图中的编号
int find(int x) { return (x == fa[x]? x : fa[x] = find(fa[x])); } //一行并查集
bool cmp(Edge a, Edge b) { return a.w < b.w; } //一行cmp

void kruskal() //克鲁斯卡尔算法:
{
	sort(edge + 1, edge + k + 1, cmp); //首先将边按权值排序
	int st = MAP(1, 1); //指定一个开始点：第一个
	int ed = MAP(n, m); //指定一个结束点：最后一个
	for(int i = 1; i <= k; i++) { //枚举边：
		int u = edge[i].u; 
		int v = edge[i].v;
		int x = find(u), y = find(v); //取出u、v所在连通块
		if(x != y) //若在同一连通块，我们就算去合并也没有多大意义，这样可以稍微节省时间
		{
			maxn = max(maxn, edge[i].w); //更新最大边权
			fa[x] = fa[y]; //将两边连通
			if(find(st) == find(ed)) return; //如果开始点和结束点连通了，说明可以退出了
		}
	}
}

int main()
{
	n = get(), m = get();
	for(int i = 1; i <= n; i++) {
		for(int j = 1; j <= m; j++) {
			p[i][j] = get();
			fa[MAP(i, j)] = MAP(i, j); //在读入的时候顺便初始化并查集
		}
	}
    //重点：连边
	for(int i = 1; i <= n; i++) {
		for(int j = 1; j <= m; j++) {
			int u = MAP(i, j); //这个点
			int v1 = MAP(i, j + 1); //向右连边
			int v2 = MAP(i + 1, j); //向下连边
            //因为是无向图，只用向两个方向连边
            //权值是两点权间的较小值
			if(j + 1 <= m) edge[++k] = {u, v1, max(p[i][j], p[i][j + 1])}; //注意判断越界。
			if(i + 1 <= n) edge[++k] = {u, v2, max(p[i][j], p[i + 1][j])};
		}
	}
	/*
	for(int i = 1; i <= k; i++) {
		printf("%d %d %d\n", edge[i].u, edge[i].v, edge[i].w);
	}
	*/
	kruskal(); //跑MST算法
	printf("%d", maxn); //输出解
	return 0;
}

Part 3 后记

前者的时间：搜索的复杂度完全就是玄学（取决于数据）

关于后者的时间？

读入、连边、快排占据了绝大部分时间，克鲁斯卡尔是线性的（可以忽略不计）。稍微卡卡常还是能跑的很快的。

经过实测，后者比前者慢、空间大、代码长······那为什么还要这么做呢？

毕竟多思考一下总是好的。

注：因为是不按常理出牌的方法，可能会有锅（虽然正确性可以得到证明）。如果您发现了HACK的方法，或者有不懂的地方，请私信作者。