自动搬运

查看原文

来自洛谷，原作者为

	GoldenSTEVE7 不拿蓝勾不改签 || GoldenSTEVE——Just do it! || 坚持变强每一天 || 半AFO

搬运于2025-08-24 21:31:31，当前版本为作者最后更新于2025-05-13 12:40:07，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题意

给定直角三角形的三边，求其较小锐角的正弦值。

思路

一个角的正弦值，即在一个直角三角形中其对边比斜边的值。

那不正好吗，题目给出的直角三角形啊！那我们就确定它的斜边和它的对边即可。

怎么求呢？我们画个草图

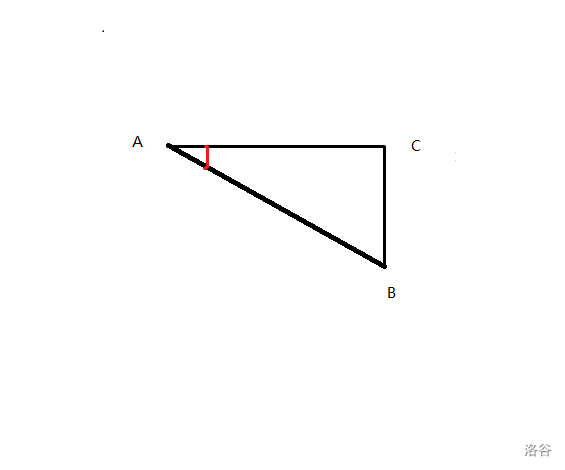
在这里，红色角是较小角，容易看出，较小角对边是较短边。

那聪明的你一定发现了，答案输出最短边比最长边即可。

但是我们还要约分，只需要将它们都除以它们的最大公约数就行了，在 c++ 中，是提供了求两个数的最大公约数的函数了的，使用方法：

__gcd(a, b)

可以求出 $(a, b)$，也就是它们的最大公约数。

那么将 $a, b$ 分别除以它们最大公约数即可。

代码

#include<bits/stdc++.h>
using namespace std;

int main() {
    int a, b, c; cin >> a >> b >> c;
    if(a > b)  swap(a, b);
    if(a > c)  swap(a, c);
    if(b > c)  swap(b, c);// 排序 a, b, c
    cout << a / __gcd(a, c) << "/" << c / __gcd(a, b); // 约分
    return 0;
}