自动搬运

查看原文

来自洛谷，原作者为

	JustinRochester **

搬运于2025-08-24 21:31:16，当前版本为作者最后更新于2018-02-14 16:13:50，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

题目

要做就要做到最好——沃·兹基硕德

为了带给大家最好的题解体验，本蒟蒻重新做了该题 $11$ 遍，接下来的内容个人感觉应该会比较适合各位食用

以前的分析我就不改了，各位跳到第一条代码下面即可

---

【分析】

法一

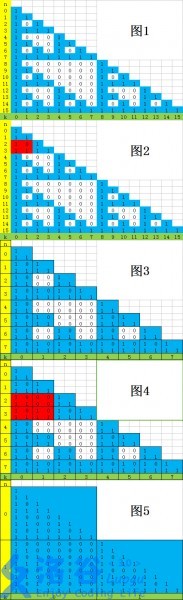
这题其实可以暴力，优雅一点就直接过了。本蒟蒻就先根据题目，打了个表。如图1所示。（真·打表）

根据图1，我们可以很清晰地看到该图是由复制得来的。于是，我们的题目就转变为，给定坐标(n,k),求该点在复制得来的图中是否是蓝色。是，则输出 $1$ ；否，则输出 $2$ 。

我们可以将其中的四个小单元格合并为一个单元。则得到结论1：单元的右上角为偶数（如果存在的话）。

又如图而得，单元的右上角满足n为偶数且k为奇数

故结论1：若( (!(n&1)) & (k&1) ) 则答案为0。

接着，因为每一个单元我们都进行了判断，所以我们可以将所有的单元都视为单元格，并重新标记n、k。结果如图3所示。

参照上面的思路，我们又可以建立新的单元，并且又能得到结论1。如图4所示。

由图1到图3的变化得，当整个图如图5所示时，判断完毕。（图5右上方不存在）。

整理一下思路：我们从图中得：若( (!(n&1)) & (k&1) ) 则答案为0，否则将n/2,k/2，循环至n<2为止。

---

【代码】

本蒟蒻代码奉上：

#include<cstdio>
#include<cctype>
using namespace std;
int read(){
	int abs=0;char c=getchar();while(!isdigit(c)) c=getchar();
	while(isdigit(c)) {abs=abs*10+c-'0';c=getchar();}
	return abs;
}//读入优化
int main(){
	int t=read();
	while(t--){
		int n=read(),k=read();
		bool i=1;
		while(n>=2&&i){
			if((!(n&1))&(k&1)) i=0;//x&1==1则x为奇数
			n>>=1;k>>=1;//x>>=1等效于x/=2
		}
		putchar(i?'1':'0');
		putchar('\n');
	}
	return 0;
}

复杂度 $O(T\log n)$

---

以下代码为本蒟蒻直接手打的。

如有错误，请在评论区直接公布或者与本蒟蒻联系。

如对众位的阅读体验感产生不良影响，本蒟蒻先再次表示歉意。

---

【分析】

法二

在学习了卢卡斯定理后，本蒟蒻重新回来做了该题

首先，根据卢卡斯定理的内容(证明本蒟蒻不会......OI不需要证明......)

$C_n^m \% p=C_{\lfloor {n \over p} \rfloor}^{ \lfloor {m \over p} \rfloor }C_{n \% p}^{m \% p} \% p$

其中 $p$ 是质数， $\lfloor x \rfloor$ 代表实数 $x$ 的向下取整

当然，由于 C++本身除法就是向下取整的，所以我们可以直接这么理解：

$C_n^m\%p=C_{n/p}^{m/p}C_{n\%p}^{m\%p}\%p$

而题目要求所求的 $C_n^k$ 的奇偶性(奇数为 $1$ , 偶数为 $0$)，显然就是求 $C_n^k \% 2$ 的值

people &me=LRJ("想一想，为什么？");

好，那么根据卢卡斯定理， $2$ 又是质数 ，我们可以直接这么计算答案：

$C_n^k\%2=C_{n/2}^{m/2}C_{n\%2}^{m\%2}\%2$

当然，众所周知 $C_0^0=C_1^0=C_1^1=1,C_0^1=0$

即 $0$ 个东西中选 $0$ 个的方案数为 $1$ ，选 $1$ 个为 $0$ (不存在该方案)

$1$ 个东西中选 $0$ 个的方案和选 $1$ 个的方案数都是 $1$

int c(int n,int k){
	if(n<=1) return (n==1)?1:((k==0)?1:0);
    return c(n/2,k/2)*c(n%2,k%2)%2;
}

复杂度 $O(T\log n)$

法三

当然，会位运算的同学这边可以优化一下，不会的可以听我讲解一下：

首先，我上面列出的四个组合数都有一个规律： $n<2$

如果懂得二进制的朋友可以想到，小于 $2$ 的数，其二进制最高位应该是最后一位。

所以说，如果我们右移一位(相当于除以 $2$)，得到的数如果不为 $0$ ，就直接说明这个数字大于等于 $2$ ，否则反之

同时，对 $2$ 取余相当于按位与上 $1$ 。因为对 $2$ 取余在二进制上就相当于取其最后一位，即按位与上除最后一位全部是 $0$ 的数—— $1$

因此，我们可以这么写，看着比较优雅 装逼

$C_n^k\&1=C_{n\&1}^{k\&1}C_{n>>1}^{k>>1}\&1$

int c(int n,int k){
    if(n>>1) return c(n>>1,k>>1)*c(n&1,k&1)&1;
	return (n&1)?1:(!(k&1));
    //k==1=>!(k&1)=!(1&1)=!1=0
    //k==0=>!(k&1)=!(1&0)=!0=1
}

复杂度 $O(T\log n)$ ，但常数比上一种小

---

法四

那么，接下来，有热情的小伙伴们还可能把 $C_{n\&1}^{k\&1}$ 拉出来讨论

为什么要讨论它呢？显然， $n\&1$、$k\&1$ 各有两种情况，一共四种，比较好讨论

1. $n\&1==1$ ，那么，不论 $k\&1$ 为什么值，$C_{n\&1}^{k\&1}=C_1^{k\&1}=1$

2. $n\&1==0,k\&1==0$，那么 $C_{n\&1}^{k\&1}=C_0^0=1$

3. $n\&1==0,k\&1==1$，那么 $C_{n\&1}^{k\&1}=C_0^1=0$

所以说 $C_n^k\&1=\begin{cases} 0,(!(n\&1))\&(k\&1)\\ C_{n>>1}^{k>>1}\&1,else\end{cases}$

int c(int n,int k){
	return ( (!(n&1))&(k&1) )?0:c(n>>1,k>>1);
}

当然，你可以去试试，这个代码是错的......

因为我们少了个递归边界： $C_0^0$

当 $n==k==0$ 时，返回 $C_{0>>1}^{0>>1}=C_0^0$，会导致栈溢出

因此，我们还要加个特判：

int c(int n,int k){
	if( !(n|k) ) return 1;
    // 当出现 c(0,0) 时，直接返回 1
    // n|k 表示 n 和 k 按位或，若两者存在不为 0 的数，则该值不为 0，取非后不为 1
	return ( (!(n&1))&(k&1) )?0:c(n>>1,k>>1);
}

复杂度 $O(T \log n)$ ，但常数理论上又要比上面小

---

法五

有的小伙伴还中意于非递归式写法，思路和上面大体一样：

当两者都不为 $0$ 时，判是否 $(!(n\&1)\&(k\&1))$ 是的话就直接返回 $0$ 了，否则 $n$,$k$ 都右移一位，直到两者为 $0$ 时返回 $1$

int c(int n,int k){
	while(n|k)
    	if( (!(n&1))&(k&1) ) return 0;
        else n>>=1,k>>=1
	return 1;
}

复杂度还是 $O(T \log n)$，但常数还能再小

---

法六

现在，众位已经很接近最优解法了

仔细看一下上面的程序：

如果用 $x_p$ 表示 $x$ 在二进制下的第 $p$ 位

那么，循环的条件显然是对于当前位 $p$ ，有$n_p==1$ 或者 $n_p==k_p$

这边有一个比较神奇的写法： $n_p\&k_p=k_p$

假设有同学懂得集合的话可以这么理解：

有个集合是 $n_p$， 一个是 $k_p$

而循环的条件相当于 $Card(n_p)==1\geq Card(k_p)$ 或者 $Card(n_p)==0==Card(k_p)$

即 $Card(n_p)\geq Card(k_p)$ ，在本题中可以直接视为 $k_p \subset n_p$

根据集合的性质，易得 $k_p\bigcap n_p=k_p$

用位运算来描述即是 $k_p\&n_p=k_p$

这一步即接下来的每一步都可以代入值想想，都要先想通来再往下看

那么，循环是不是表示说我从后往前枚举每一位，如果 $n_p\&k_p=k_p$ 那么继续循环，否则就直接判 $0$

也就是说：如果存在 $n_p\&k_p\neq k_p$ ，那么，答案为 $0$

如果说 $k$ 中存在 $k_p$ 使得 $n_p\&k_p\neq k_p$ ,那么，是不是说明一定有 $k\&n \neq k$ ？

所以说如果 $k\&n \neq k$ 可以直接判 $0$ 跳出

而对于 $k\&n==k$ 的情况，我们是不是可以这么去想它：

首先， $n$ 的位数一定大于等于 $k$ ，否则该情况肯定不成立

其次，我们如果把 $k$ 的不足的位数全部补 $0$ ，是不是就显然有对于 $k$ 中的任意位置 $p$ 都有 $n_p\&k_p=k_p$ ？

所以，循环会一直进行，当 $k$ 补充的位数也全部用完， $n$ 的全部位数也用完了

也就是说，此时 $n|k==0$

因此，跳出循环，返回 $1$

综上，答案就是： $(n\&k==k)?1:0$

或者可以直接把该函数打成 $bool$ 型的

bool c(int n,int k){ return n&k==k; }

因此，对于每次询问都是 $O(1)$ 的，总复杂度 $O(T)$

至此，对于 $O(1)$ 计算答案的全证明过程结束

---

还有小伙伴有疑问： 万一我考试的时候想不到怎么办？

不用方，这边再介绍最后一种方法：

如果我们知道 $C_n^m$ 中因数 $2$ 的个数，显然可以知道它的奇偶性

如果因数 $2$ 为 $0$ 个，即为奇数，否则为偶数

同时，我们还知道 $C_n^m={n ! \over m!(n-m)!}$

所以说，如果我们用 $two_i$ 表示 $i$ 的因数中 $2$ 的个数

那么，显然有 $two_{C_n^m}=two_{n!}-two_{m!}-two_{(n-m)!}$

如果说我们知道右边三个数的答案，对于 $C_n^m$ 是奇是偶就可以 $O(1)$ 判断了

那么我们还可以知道什么呢？

首先 $two_{i!} \geq two_{(i-1)!}$

当且仅当 $i$ 为奇数时取等，因为 $i$ 不含因数 $2$ ，故 $two_{i!}=two_{(i-1)!}+0$

当 $i$ 为偶数时，暴力地去判断它因数中 $2$ 的个数，即如果除以 $2$ 余 $0$ ，就是还含有因数 $2$ ，就计数器 $+1$, 该数除以 $2$

有看我上面的小伙伴还能想到位运算：当该数 $\&1$ 非 $0$ 时，该数右移 $1$，且计数器 $+1$

int two[100010]={0};//这边的 two[i] 表示的是 two[i!] 的
void pre(){
	for(int i=1;i<=100000;i++){
    	two[i]=two[i-1];
        int tmp=i;
        while(tmp&1) tmp>>=1,two[i]++;
    }
}

这样就可以实现 $O(1)$ 查询了，预处理的复杂度是 $O(n)$ 的，总复杂度是 $O(T+n)$

由于 $T$ 与 $n$ 同阶，可以近似地认为是常数较大的 $O(T)$

这边给出预处理复杂度的证明(昨晚想了一宿)：

对于每一个数，都会进行一次将上一个值赋值过来的操作，该操作进行 $n$ 次

对于 $2$ 的倍数，除赋值外还需自增一次，该操作进行 $\lfloor {n \over 2} \rfloor$ 次

对于 $4$ 的倍数，还需再自增一次，该操作 $\lfloor {n \over 4} \rfloor$ 次

对于 $8$ 的倍数，又需再自增一次，$\lfloor { n\over 8} \rfloor$ 次

因此，总操作数为：

$n+\lfloor { n\over 2} \rfloor+\lfloor { n\over 4} \rfloor+\lfloor { n\over 8} \rfloor+\lfloor { n\over 16} \rfloor \cdots$

$\approx n+{ n\over 2}+{ n\over 4}+{ n\over 8}+{ n\over 16}\cdots$

$=2n$

因此，预处理复杂度为 $O(n)$

---

觉得写得不错的麻烦点个赞吧......

写了一整节晚自习呢

最后安利一下 本蒟蒻的博客