自动搬运

查看原文

来自洛谷，原作者为

	wucstdio 这个家伙不懒，但还是什么都没留下

搬运于2025-08-24 21:31:08，当前版本为作者最后更新于2018-04-24 19:32:52，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

线段树扫描线详解

基本思想

比如，对于下面的三个矩形：

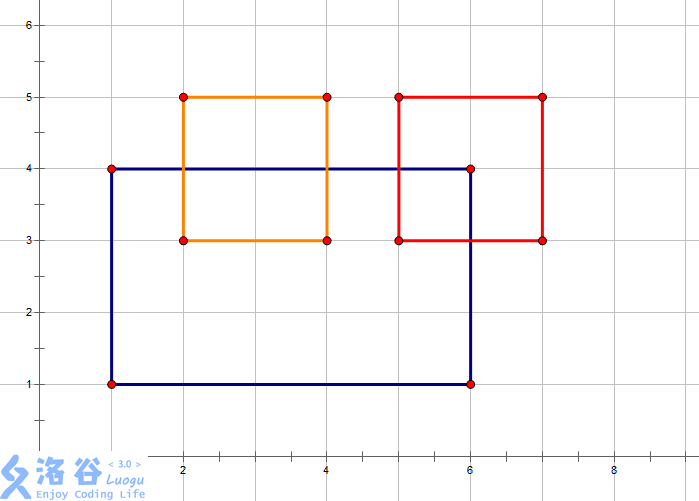
想象有一条扫描线，从下往上扫描完整个图案，每遇到一条上边或者下边就停下来：

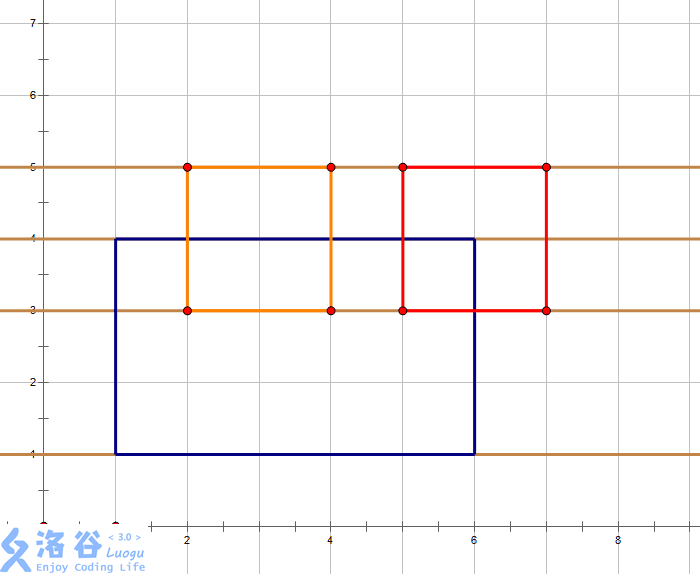
然后每次停下后对区间进行处理，用一个ans代表当前周长，最后ans就是答案。

代码实现

首先，要先把矩形拆成上边和下边，用1和-1分别代表下边和上边。然后按高度排序，这样数组从前往后处理就相当于扫描线从下往上扫描。如果是下边，就在对应区间上加1，如果是上边，就在对应区间上减1。

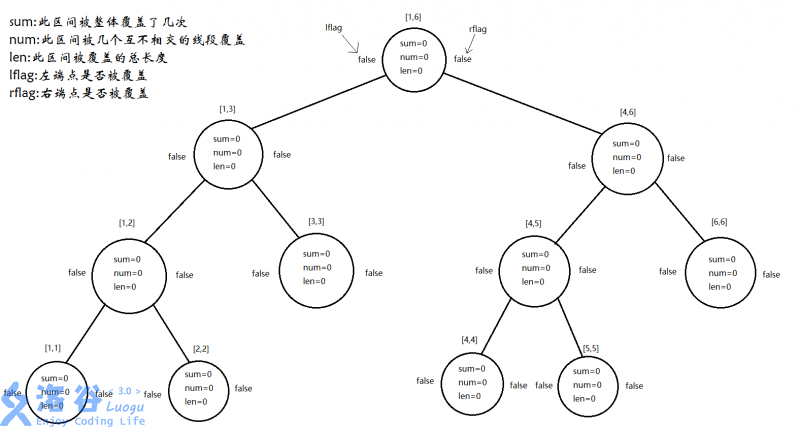
在整个区间上建一棵线段树：

#define lson o<<1
#define rson o<<1|1
#define mid (l+r)/2
struct Tree
{
    int sum;//整个区间被整体覆盖了几次（类似lazytag，但不下传)
    int num;//整个区间被几条互不相交的线段覆盖（比如，[1,2],[4,5]则为2，[1,3],[4,5]则为1（我习惯用闭区间），[1,4],[2,2],[4,4]也为1）
    int len;//整个区间被覆盖的总长度
    bool lflag;//左端点是否被覆盖（合并用）
    bool rflag;//右端点是否被覆盖（合并用）
}//如果不懂也没有关系，接着往下看

那么pushup要怎么写呢？

void pushup(int o,int l,int r)
{
	if(tree[o].sum)//此区间之前被一整个线段覆盖过
	{
		tree[o].num=1;
		tree[o].len=r-l+1;
		tree[o].lflag=tree[o].rflag=1;
	}
	else if(l==r)//这是一个叶节点
	{
		tree[o].num=0;
		tree[o].len=0;
		tree[o].lflag=tree[o].rflag=0;
	}
	else//一般情况
	{
		tree[o].num=tree[lson].num+tree[rson].num;
		if(tree[lson].rflag&&tree[rson].lflag)tree[o].num--;//flag的用处
		tree[o].len=tree[lson].len+tree[rson].len;
		tree[o].lflag=tree[lson].lflag;
		tree[o].rflag=tree[rson].rflag;
		//注意：sum不会被修改，只有当它被一整个线段覆盖时才会修改
	}
}

有了pushup，add函数就好写了：

void add(int o,int l,int r,int from,int to,int value)//此区间为[l,r],待修改区间为[from,to]，添加值为value。
{
    if(l>=from&&r<=to)//被整个覆盖
    {
        tree[o].sum+=value;
        pushup(o,l,r);
        return;
    }
    if(from<=mid)add(lson,l,mid,from,to,value);
    if(to>mid)add(rson,mid+1,r,from,to,value);
    pushup(o,l,r);
}

流程

Step 0：build

Step 1：add(1,1,6,1,5,1)

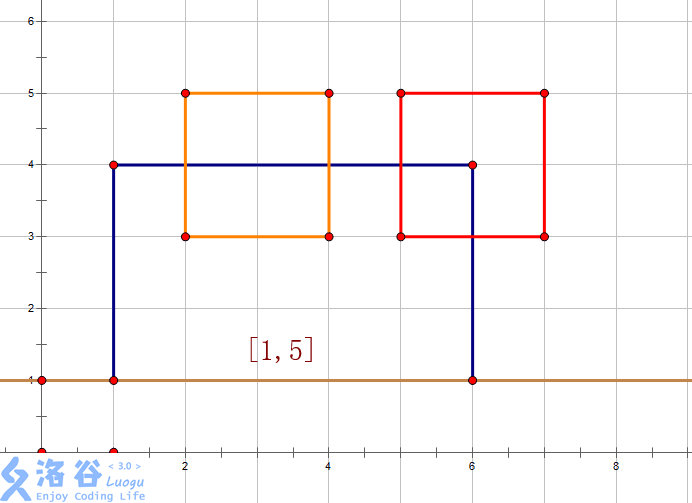
先递归处理：

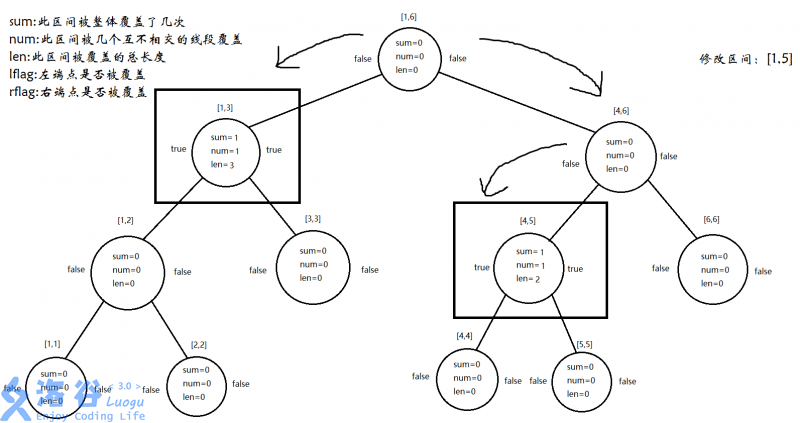
再pushup：

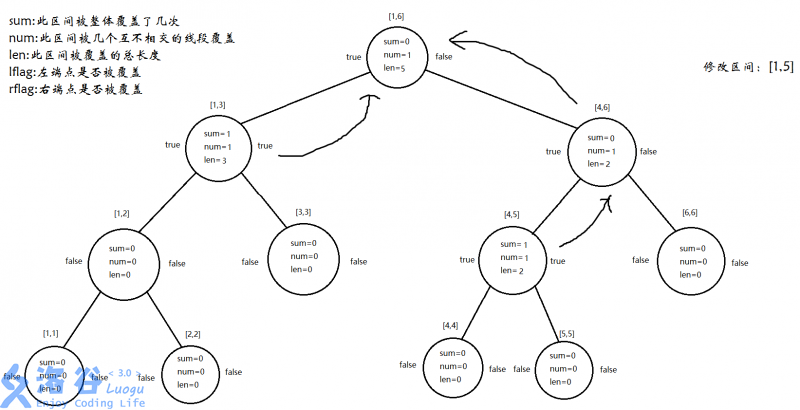
Step 2:add(1,1,6,2,3,1)

Step 3:add(1,1,6,5,6,1)

(懒得分开写了）

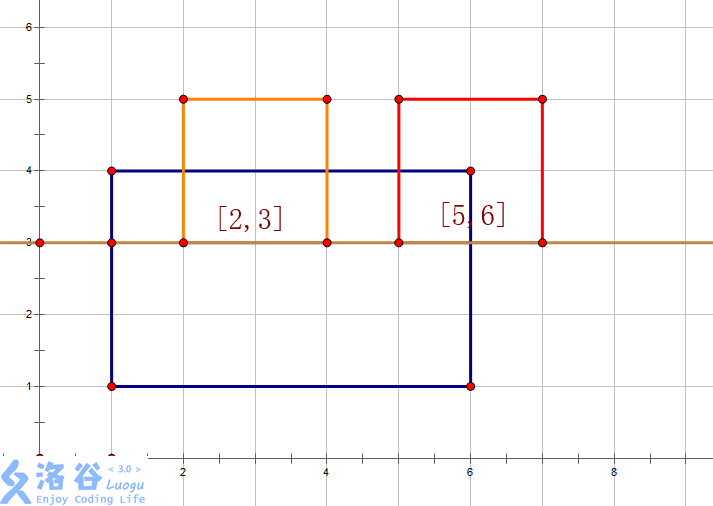
递归处理，pushup：

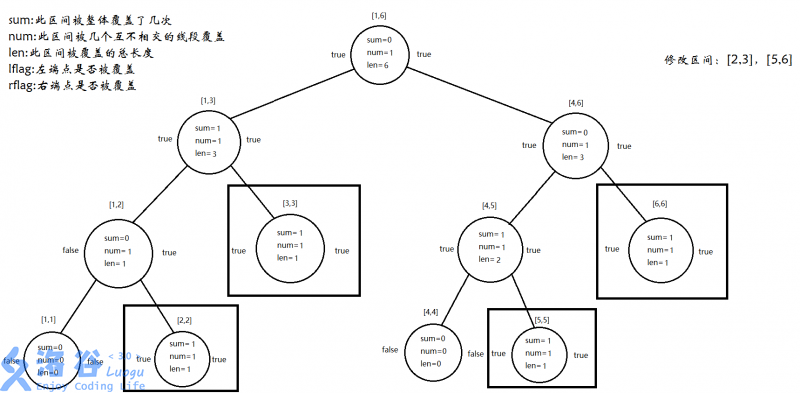
Step 4:add(1,1,6,1,5,-1)

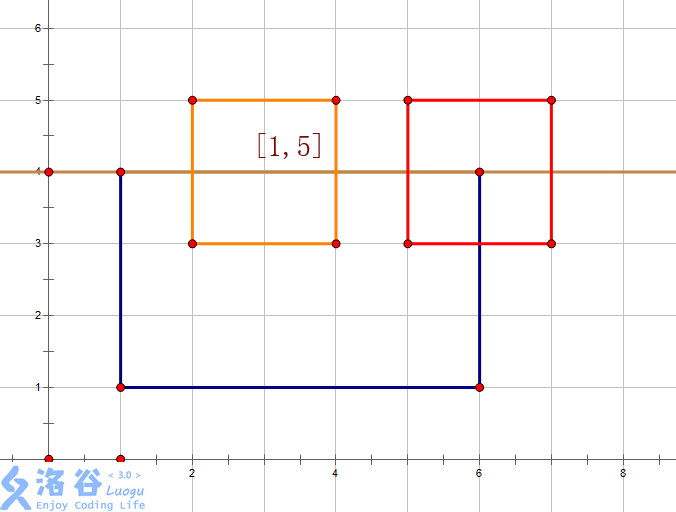
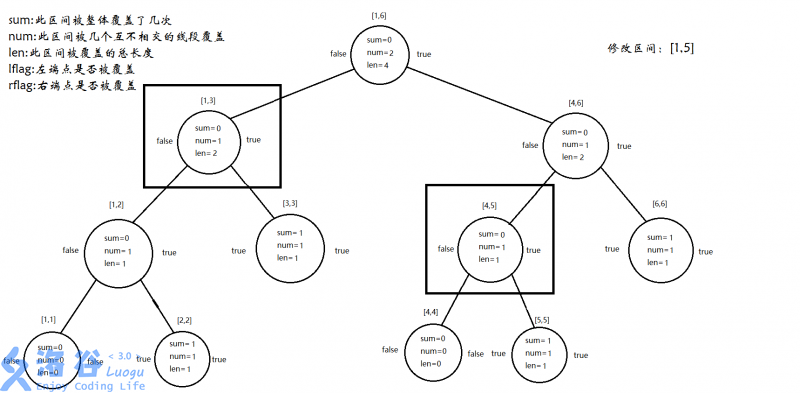
Step 5:add(1,1,6,2,3,-1)

Step 6:add(1,1,6,5,6,-1)

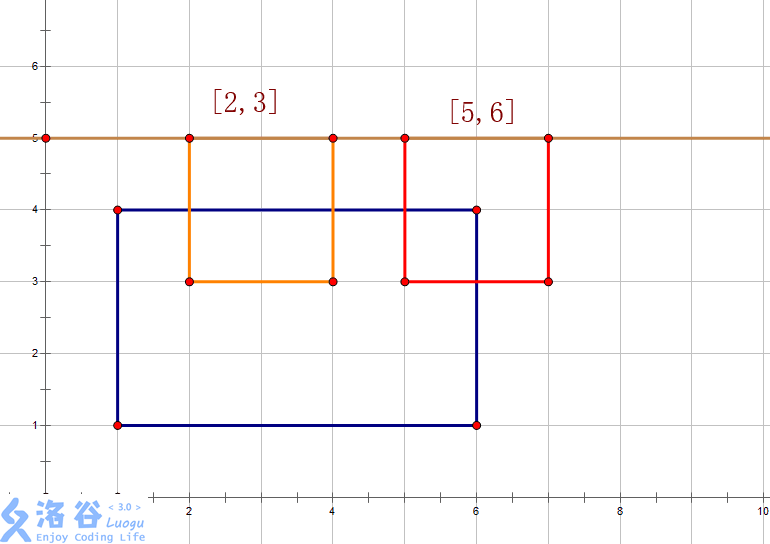
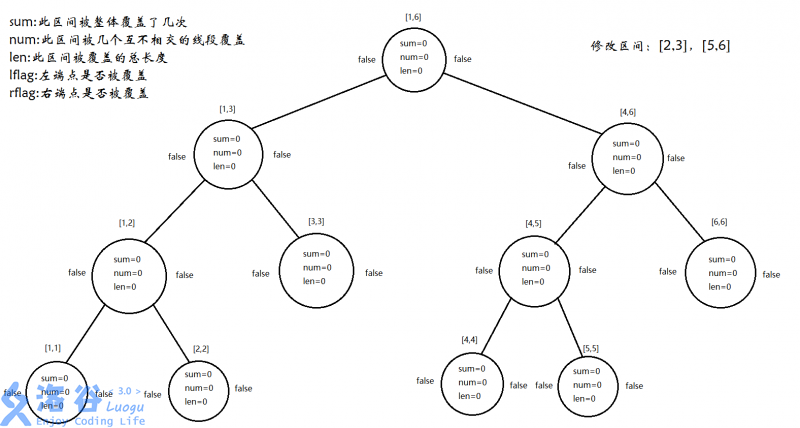
至此，总算说完了线段树的修改。

答案统计

突然想起一个很严肃的事情来：答案怎么统计？

对于横边，相邻两次修改的区间覆盖长度差（就是tree[root].len的差）加起来就是答案（不理解的自己想办法理解，反正我不理解）；

对于竖边，你可以再让扫描线从左到右扫一遍~~不过还是说简单法吧。我们需要记录整个区间有多少个端点（包含在线段内不算），然后用它乘上相邻两次修改的高度差。

怎么记录呢？

对了，就是$tree[root].num*2*(h2-h1)$（num的作用在这里）

好了，下面是完整代码：

#include<cstdio>
#include<algorithm>
#include<cstring>
#define lson o<<1
#define rson o<<1|1
#define mid (l+r)/2
using namespace std;
struct Edge
{
	int left;
	int right;
	int height;
	int flag;
}e[10005];
struct Tree
{
	int sum;
	int num;
	int len;
	bool lflag;
	bool rflag;
}tree[100005];
int n,mx=-2147483647,mn=2147483647,edgenum,ans,last;
void add_edge(int l,int r,int h,int f)
{
	e[++edgenum].left=l;
	e[edgenum].right=r;
	e[edgenum].height=h;
	e[edgenum].flag=f;
}
bool cmp(Edge a,Edge b)
{
	return a.height<b.height||a.height==b.height&&a.flag>b.flag;
}
void pushup(int o,int l,int r)
{
	if(tree[o].sum)
	{
		tree[o].num=1;
		tree[o].len=r-l+1;
		tree[o].lflag=tree[o].rflag=1;
	}
	else if(l==r)
	{
		tree[o].len=0;
		tree[o].num=0;
		tree[o].lflag=tree[o].rflag=0;
	}
	else
	{
		tree[o].len=tree[lson].len+tree[rson].len;
		tree[o].num=tree[lson].num+tree[rson].num;
		if(tree[lson].rflag&&tree[rson].lflag)tree[o].num--;
		tree[o].lflag=tree[lson].lflag;
		tree[o].rflag=tree[rson].rflag;
	}
}
void add(int o,int l,int r,int from,int to,int value)
{
	if(l>=from&&r<=to)
	{
		tree[o].sum+=value;
		pushup(o,l,r);
		return;
	}
	if(from<=mid)add(lson,l,mid,from,to,value);
	if(to>mid)add(rson,mid+1,r,from,to,value);
	pushup(o,l,r);
}
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		int x1,y1,x2,y2;
		scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
		mx=max(mx,max(x1,x2));
		mn=min(mn,min(x1,x2));
		add_edge(x1,x2,y1,1);
		add_edge(x1,x2,y2,-1);
	}
	if(mn<=0)
	{
		for(int i=1;i<=edgenum;i++)
		{
			e[i].left+=-mn+1;
			e[i].right+=-mn+1;
		}
		mx-=mn;
	}
	sort(e+1,e+edgenum+1,cmp);
	for(int i=1;i<=edgenum;i++)
	{
		add(1,1,mx,e[i].left,e[i].right-1,e[i].flag);//注意这里！！！加边有学问！！！
		while(e[i].height==e[i+1].height&&e[i].flag==e[i+1].flag)
		{
			i++;
			add(1,1,mx,e[i].left,e[i].right-1,e[i].flag);
		}
		ans+=abs(tree[1].len-last);
		last=tree[1].len;
		ans+=tree[1].num*2*(e[i+1].height-e[i].height);
	}
	printf("%d\n",ans);
	return 0;
}

最后给两个卡死我的样例：

样例输入1：

7
-15 0 5 10
-5 8 20 25
15 -4 24 14
0 -6 16 4
2 15 10 22
30 10 36 20
34 0 40 16

样例输出1：

228

样例输入2：

2
0 0 4 4
0 4 4 8

样例输出2：

24