自动搬运

查看原文

来自洛谷，原作者为

	LlLlCc 背井离乡，忍辱负重

搬运于2025-08-24 21:31:05，当前版本为作者最后更新于2020-05-26 20:24:00，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

不得不说，这题建模极为抽象了，出题人太神了。看了好多篇题解才懂，自己也写一篇比较详细的吧

---

相信大家都玩过跳棋，有一个规则想必大家都知道，就是一次跳跃不能跳过两颗棋子

这个限制是解决这题的关键，有了这个限制，可以看出，对于两边的棋子，只能跳到其余两颗的中间，同样的中间的棋子也只能跳到两边

为了方便，我们将三个棋子标号，分别为$x,y,z$，且$x<y<z$。

移动棋子无非就四种讨论

• $\large(x,y,z)\implies(2x-y,x,z)$

• $\large(x,y,z)\implies(x,z,2z-y)$

• $\large(x,y,z)\implies(y,2y-x,z)$

• $\large(x,y,z)\implies(x,2y-z,y)$

因为有了不能一次跳过两颗棋的限制，所以第三种情况和第四种情况必然起了冲突

不妨设$d1=y-x,d2=z-y$，易得

• $d1<d2:$则 $(x,y,z)\implies(y,2y-x,z)$

• $d1>d2:$则 $(x,y,z)\implies(x,2y-z,y)$

也就是说我们对于每种状态只有三种转移方式

我们再看看这三个式子，可以发现，对于第一种和第二种情况，我们将中间的点向两边跳，相当于扩大了边界。而第三种两边向里面跳则恰恰相反，是将边界缩小了

是不是很像一棵二叉树？

现在可能还不够明显，我们再接下去推

有一个很显然的性质，边界不可能无限变小。也就是说缩着缩着会遇到一种情况不能再缩了，我们来思考一下什么情况不能再缩了

观察式子：

• $d1<d2:$则 $(x,y,z)\implies(y,2y-x,z)$

• $d1>d2:$则 $(x,y,z)\implies(x,2y-z,y)$

惊奇的发现，我们这样讨论漏了一种情况，$d1=d2$

这个非常好理解，如果$d1=d2$，那么$x$必然会与$z$跳到同一个点，而这是不符合题目描述的。所以当$d1=d2$时，这个状态只能由中间向两边跳，也就是只有两个转移状态，想想这个状态在二叉树中像什么？没错，根节点我们就这样找到了，二叉树的形态就像下图所示：

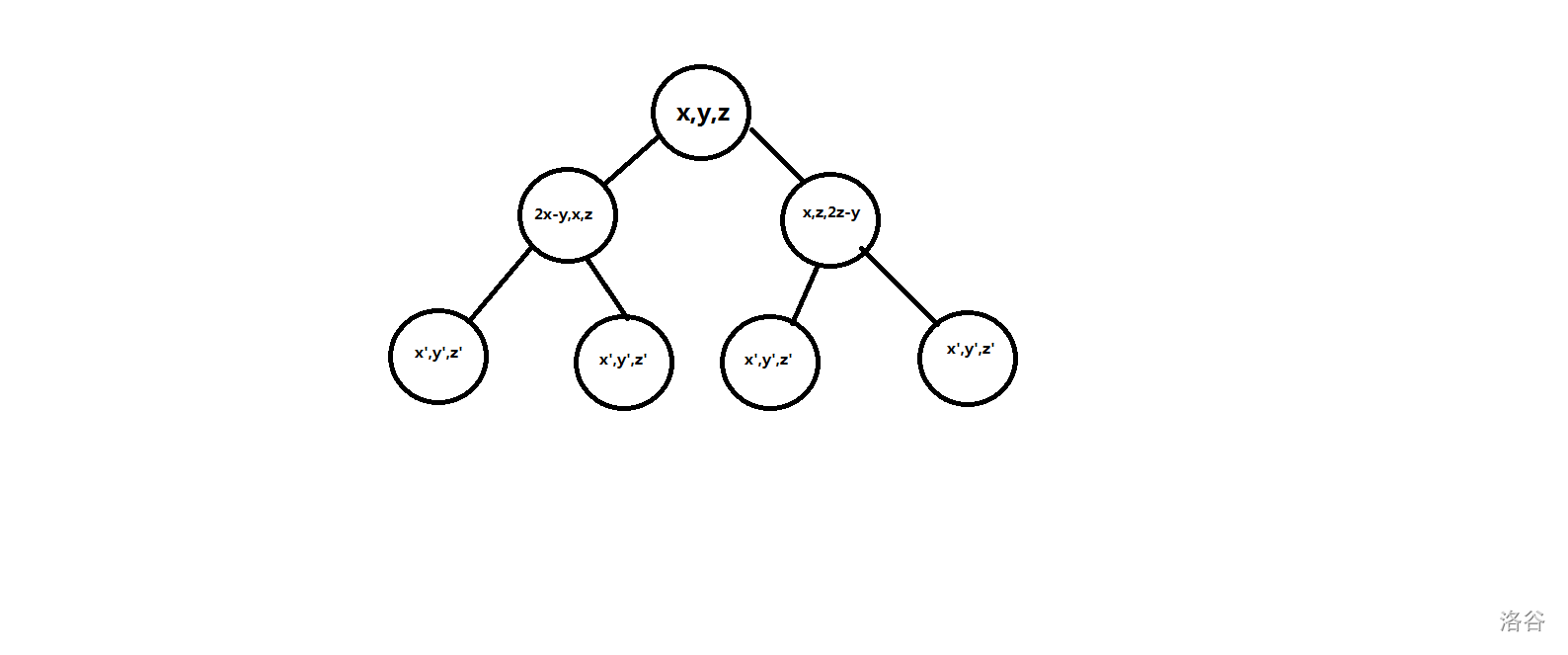
可以发现，对于每一组$(x,y,z)$都有唯一对应的一个根，而且二叉树之间的任意一组$(x,y,z)$都可以互相转化，而且转化的操作次数就等于两个状态在树上的距离

所以如果初始$(x,y,z)$的树根和目标$(x',y',z')$的树根不相同，那么就是$No$，因为无论怎么跳都出不去这棵树的范围，而根不同则说明树不同

所以对于初始$(x,y,z)$和目标$(x',y',z')$，我们只要求出它们的$LCA$，答案就是初始点到$LCA$的距离$+$ $LCA$到目标点的距离

不过因为范围太大，树无法存下，普通的$LCA$求法树剖、倍增等已经无法使用了

我们先不急着求$LCA$，来想想另一个问题

初始状态：$(1,10,11)$

目标状态：$(1,2,3)$

人脑模拟一下程序，$d1>d2$，转换成$(1,9,10)$，$(d1>d2)$，转换成$(1,8,9)$，$d1>d2$，转换成$(1,7,8)$,$\cdots\cdots$

如果改成$(1,inf-1,inf)$呢？

显然要$T$飞

不过我们发现，一直在重复一个操作，所以可以将这些操作压缩

我们只讨论$d1>d2$的情况，$d1<d2$其实差不多

易发现，要连续跳$(d1-1)/d2$次同样的操作（每一次跳$d2$的距离，但又不能超越或跳到$x$，也就是总距离为$(d1-1)$，总次数故为$(d1-1)/d2$）

设：$d3=(d1-1)/d2$

所以最后是$\large(x,y-d3\cdot d1,z-d3\cdot d1)$

这样我们就大大的压缩了路径，但这样又有什么用呢？我们回到树上来

因为路径被压缩了，所以我们可以换种方法求$LCA$

方便起见，我们先将初始状态跳到和目标状态在树中的高度一致（如果目标状态高度更高我们就换一下，在树中的距离是没有方向的）

也是初始状态要向上跳$Dep_T-Dep_S$次（$Dep$表示深度，$S$和$T$分别表示起始状态和目标状态），而跳跃的操作我们就可以用压缩路径快速实现

好了，现在两个状态高度相同了

有个显然的性质，如果两个状态同时向上跳$x$次所跳到的节点相同，那么同时向上跳$x+1$次所跳到的节点也相同，也就是说明满足单调性。所以我们可以用二分来枚举最小的$x$满足了两个状态同时向上跳$x$次所跳到的节点相同，所以$LCA$就是两个同时向上跳$x$次所跳到的节点

然后就愉快的$AC$了

码量小但细节是真的多，思维难度也很好，总而言之就是一道质量非常高的建模$LCA$+二分的题目

如果有哪步我打错了，或者有一些没有理解的地方，欢迎私信或留言！

参考代码：

#include<bits/stdc++.h>
using namespace std;
int Cnt,Ans,d1,d2,d3,x,y,z,L,R,X,Y,Z,tot,a[5];
struct lc{
	int x,y,z,tot;
}A,B;
inline int read(){
	int ret=0,f=1;char ch=getchar();
	while (ch<'0'||ch>'9'){if (ch=='-') f=-f;ch=getchar();}
	while (ch<='9'&&ch>='0') ret=ret*10+ch-'0',ch=getchar();
	return ret*f;
}
inline void Dfs(int x,int y,int z){
	tot=0;
	while (1){
    	d1=y-x,d2=z-y;
    	if (d1==d2) break;
    	if (d1>d2) d3=(d1-1)/d2,tot+=d3,y-=d3*d2,z-=d3*d2;
    	else d3=(d2-1)/d1,tot+=d3,x+=d3*d1,y+=d3*d1;
	}
	if (A.x||A.y) B=(lc){x,y,z,tot};
	else A=(lc){x,y,z,tot};
}
inline void Swap(){
	swap(x,X),swap(y,Y),swap(z,Z);
	swap(A.x,B.x),swap(A.y,B.y),swap(A.z,B.z),swap(A.tot,B.tot);
}
inline bool check(int T,int x,int y,int z,int X,int Y,int Z){
	tot=T;
	while (tot){
    	d1=y-x,d2=z-y;
    	if (d1==d2) break;
    	if (d1>d2) d3=min((d1-1)/d2,tot),tot-=d3,y-=d3*d2,z-=d3*d2;
    	else d3=min((d2-1)/d1,tot),tot-=d3,x+=d3*d1,y+=d3*d1;
	}
	tot=T;
	while (tot){
    	d1=Y-X,d2=Z-Y;
    	if (d1==d2) break;
    	if (d1>d2) d3=min((d1-1)/d2,tot),tot-=d3,Y-=d3*d2,Z-=d3*d2;
    	else d3=min((d2-1)/d1,tot),tot-=d3,X+=d3*d1,Y+=d3*d1;
	}
	return X==x&&Y==y&&Z==z;
}
int main(){
	for (int i=1;i<=3;i++) a[i]=read();
	sort(a+1,a+4);x=a[1],y=a[2],z=a[3];
	for (int i=1;i<=3;i++) a[i]=read();
	sort(a+1,a+4);X=a[1],Y=a[2],Z=a[3];
	Dfs(x,y,z);Dfs(X,Y,Z);
    if (A.x!=B.x||A.y!=B.y||A.z!=B.z){printf("NO");return 0;}
    if (A.tot<B.tot) Swap();
    Ans=tot=A.tot-B.tot;
    while (tot){
    	d1=y-x,d2=z-y;
    	if (d1==d2) break;
    	if (d1>d2) d3=min((d1-1)/d2,tot),tot-=d3,y-=d3*d2,z-=d3*d2;
    	else d3=min((d2-1)/d1,tot),tot-=d3,x+=d3*d1,y+=d3*d1;
	}
	L=0,R=B.tot;
	while (L<=R){ 
		int mid=L+R>>1;
		if (check(mid,x,y,z,X,Y,Z)) Cnt=mid,R=mid-1;
	    else L=mid+1;
	}
	printf("YES\n%d",Ans+Cnt*2);
	return 0;
}