自动搬运

查看原文

来自洛谷，原作者为

	3493441984zz **

搬运于2025-08-24 21:30:23，当前版本为作者最后更新于2019-02-15 09:50:24，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

贪心$+$双向链表

思路真的很神奇，我做过了这种题目但是看的第一眼还是想不到这种办法，太弱惹呜呜呜

最开始的思路：

虽然最近做过这种贪心题，但是苦思冥想后还是做不出，于是重新看一遍题目呀，发现，这不是一道$dp$吗，小菜吧，于是我兴高采烈的看了一下数据范围，$QAQ$，我这种蒟蒻写的$dp$肯定会爆空间，于是使用秘术：看题解$qwq$

思路：

看完题解后，其实讲的有点模糊，所以来写一篇题解，希望能讲清

在这里先膜拜一下题解里的$dalao$，这种思路都想得出

那么言归正传

我们先观察这一道题，要求最大值，那么我们先来看一种错误的做法(注意是错误的)：

先用优先队列处理每个点（大根堆）

我们对于每一次种树，取美观度最大值种树，然后标记两旁访问过，访问过的地方就不种树

那么可能一开始都这么想~~（可能并不是）~~，然而这种做法错在哪里呢：

假如是这种情况（$4$个点中取$2$个）：

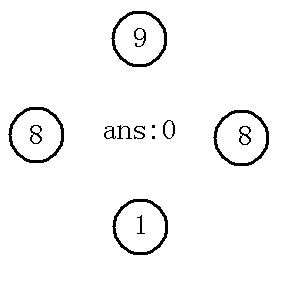
我们按照上面的做法取的话，会是下图的结果

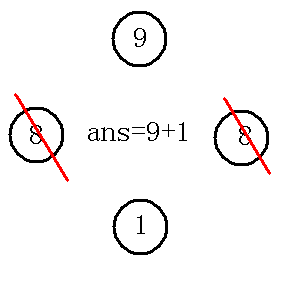
那么我们发现了一个问题:

我们取最大值的时候，可能取两边的会比取中间的更优！

那么为了处理这个问题，我们可以这样做：

一开始对于每个点建立双向链表

当前取了这个点后，把它出优先队列的同时，再加入一个点，这个点的权值是左边点权$+$右边点权$-$当前点权，例如上图：

当我们取了$9$后，我们应该加一个点，点权为$8+8-9=7$，并且把双向链表更新，$9$的左边变为$8$的左边$1$，右边同理

为什么这样弄呢？为什么这样就能解决上面的问题呢？

其实我们这样做是添加了一个反悔机制，我们来模拟一下上图：

当我们把$7$入队列，$9$出队列后，图就变成下图了：

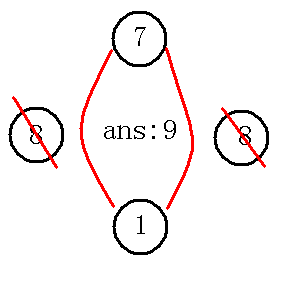
那么由于是优先队列，下一个出来的是$8$，但是$8$被访问过了，（在$9$出队列的时候，左右都标记为访问了），那么直接退出，下一个出队列的是$8$，也被访问过了，退出，下一个出队列的是$7$，没被访问，更新$ans$，并且把左右两边置为访问过，也就是下图：

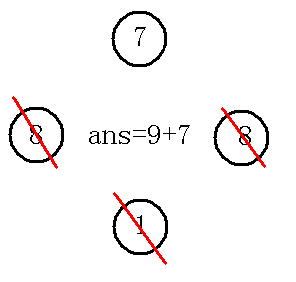
由于取了两次了，退出，那么最后的答案就是$16$也就是$9+7$，但是我们发现$16$也等于$8+8$，那么这整个过程其实就相当于我们取了$8,8$,因为我们一开始取了$9$，然后取了$7$，但是$7$是怎么来的呢，就是$8+8-9$来的，那么$9+7$就可以化为$9+8+8-9$，也就是$8+8$,所以你看懂这个反悔机制了吗

下面是美滋滋的代码时间~~~

// luogu-judger-enable-o2
#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
#define N 200007
using namespace std;
struct Place
{
	int val,l,r;
	
}p[N];
struct Node
{
	int val,id;
	bool operator <(Node it) const
	{
		return val<it.val;
	} 
};
int n,m,ans;
bool vis[N];
priority_queue<Node> q;
void Del(int x)
{
	p[x].l=p[p[x].l].l;
	p[x].r=p[p[x].r].r;
	p[p[x].l].r=x;
	p[p[x].r].l=x;
}
int main()
{
	scanf("%d%d",&n,&m);
	if(n<m*2)
	{
		printf("Error!");
		return 0;
	}
	for(int i=1;i<=n;++i)
	{
		scanf("%d",&p[i].val);
		p[i].l=i-1;
		p[i].r=i+1;
		q.push((Node){p[i].val,i});
	}
	p[1].l=n,p[n].r=1;
	for(int i=1;i<=m;++i)
	{
		while(vis[q.top().id])
			q.pop();
		Node now=q.top();
		q.pop();
		ans+=now.val;
		vis[p[now.id].l]=vis[p[now.id].r]=1;
		p[now.id].val=p[p[now.id].l].val+p[p[now.id].r].val-p[now.id].val;
		q.push((Node){p[now.id].val,now.id});
		Del(now.id);
	}
		
	printf("%d",ans);
	return 0;
}