1 条题解
-
0
自动搬运
来自洛谷,原作者为

jzzcjb
**搬运于
2025-08-24 21:28:47,当前版本为作者最后更新于2018-09-22 08:05:50,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
今天把这道题刚过去了,写篇题解纪念一下。
发现因为数据水,所以有些并没有考虑全情况的代码也AC了。
我的方法比较容易懂。写一篇自认为正确的题解,有错轻喷。
Step 0
先看懂题意,题目中的从上往下看是指把纸竖过来,从轴正方向的位置往下看,所有的正方形都变成了一段段线段,其中有多少个正方形(变成的线段)能被看到。原来的这4个正方形从上面看是这样的,
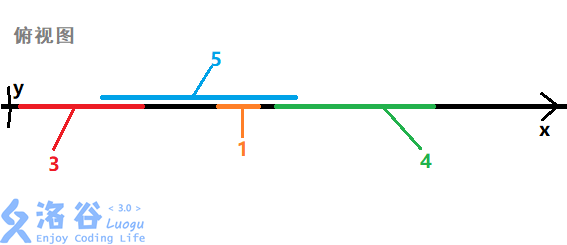
对齐之后
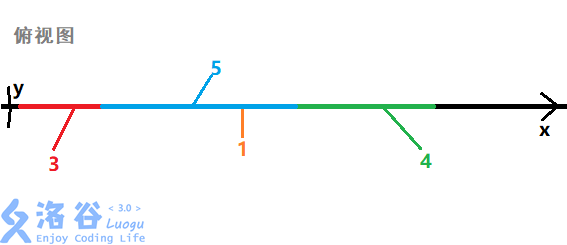
黄色的那一小段 就被左边的 和右边的 盖住了,所以输出 。
依次 就是不能越过上一个正方形。就像样例中的 没有插到 , 中间的空的意思。这意味着,一旦给定每个正方形的边长,那么它们的放置情况就是一定的了。
这给了我们思路,可以依次把这 个矩形都放置好,再计算那些能被看到,那些不能被看到。
Step 1
计算每个正方形应该被放到哪。
首先转化一下:
-
正方形能不能被看到与整张图的大小无关。是指把所有正方形的边长全部扩大或缩小相同的倍数不会改变它们互相之间的遮盖关系
-
因为要旋转 边长乘除 不方便,还会有精度问题
所以不妨重新定义每个正方形对角线的长度为“边长”,并且以相同的刻度对 轴的刻度进行重置。就像这样
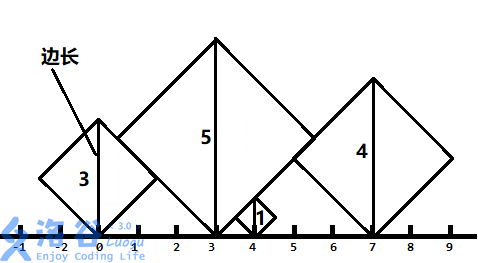
回到我们的要求:看看两个正方形相邻都有哪些形态

不难发现,两个正方形相邻的时候,只要让其中比较小的那个有一个“落脚点”即可。也就是说,只要它们之间的距离等于两者边长的较小值即可。
所以得出递推式
这样就结束了吗?考虑这样一种情况
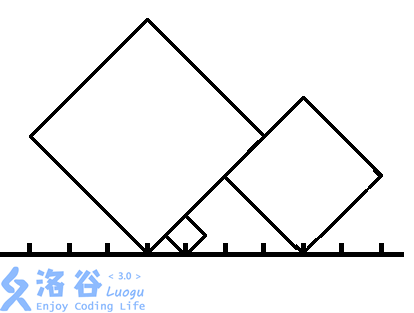
如果按上面的公式计算,就变成了
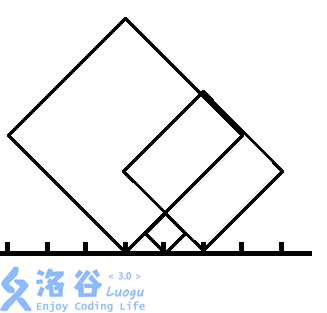
显然不对。所以,我们还要满足对于之前所有的正方形,都能让它满足存在“落脚点”,即
这样,就求了每个正方形的位置。
Step 2
计算正方形覆盖
根据对于边长的重新定义,很容易能写出一个正方形的左右两个顶点的位置 和 。
最简单的想法是如果它左边的正方形完全覆盖它,或者它右边的正方形完全覆盖它,或者两边一边覆盖一半,那么它就不会被看见了。
$$pos_{i-1}+\frac{a_{i-1}}{2}>pos_{i+1}-\frac{a_{i+1}}{2} $$但是,有这样一种情况。
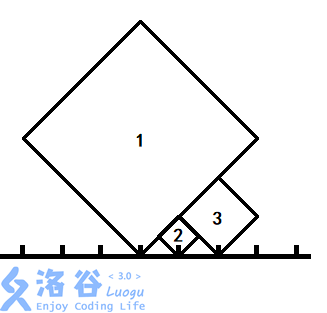
同样被挡住了,但不是被它左边的挡住的,而是被左边的左边挡住了,所以对于一个正方形我们要求出他右边所有正方形中最靠左的左端点和左边所有正方形中最靠右的右顶点。
如果两个端点接触了,则证明这个正方形被覆盖了。
要与 取 , 要与 取 。因为即使没有接上另一头,被一边单独覆盖也是不行的。
这样就结束了吗?再看一个反例
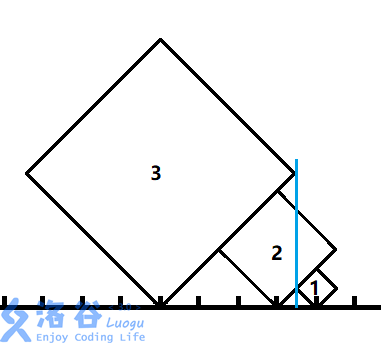
这里 很显然已经接触了,但还是能看到 。因为 在 的下面,所以即使 接触了 的右警戒线,但还是对 造不成威胁。所以计算 和 时要忽略那些比 矮的,也就是边长小与 的正方形。
还有注意 和 的初始化,一个要赋成极大值,一个要赋成极小值,不能赋成 。因为有可能某个正方形的左顶点会变为负数,这样就影响了它左边的某些正方形。
这样,这道题就被完美解决了,细节比较多,但代码很简单。
代码:
#include<iostream> #include<cstdio> #include<cstring> using namespace std; int n,a[101],p[101],R[101],L[101];//p -> pos int main(){ while(cin>>n&&n){ memset(p,0,sizeof(p)); memset(a,0,sizeof(a)); memset(L,0x3f,sizeof(L)); memset(R,0xcf,sizeof(R)); for(int i=1;i<=n;i++){ cin>>a[i];a[i]*=2;//后面有/2操作,这里要*2以逃避double for(int j=1;j<i;j++) p[i]=max(p[i],p[j]+min(a[j],a[i])); } for(int i=1;i<=n;i++){ for(int j=1;j<i;j++)if(a[j]>a[i]) R[i]=max(R[i],p[j]+a[j]/2); R[i]=max(R[i],p[i]-a[i]/2); } for(int i=1;i<=n;i++){ for(int j=i+1;j<=n;j++)if(a[j]>a[i]) L[i]=min(L[i],p[j]-a[j]/2); L[i]=min(L[i],p[i]+a[i]/2); } for(int i=1;i<=n;i++) if(R[i]<L[i]) cout<<i<<" "; puts(""); } }另外再附上刚才举反例的数据
3 7 3 1 1 2 -
- 1
信息
- ID
- 735
- 时间
- 1000ms
- 内存
- 125MiB
- 难度
- 5
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
