自动搬运

查看原文

来自洛谷，原作者为

	_H1kar1 I get no sleep,days on repeat.

搬运于2025-08-24 21:28:22，当前版本为作者最后更新于2019-07-13 01:16:03，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

说在前面：既然是没什么包装的模板题，那么建议大家打细致一些，如果不很清楚，代码量多一些也没关系，一条一条重在理解透彻

好，进入正题：

很明显的一道Tarjan，题解中讲Tarjan的神犇也有很多，但是我自认为还可以多用些图和Markdown将这个算法讲的更清楚些，所以这里重新讲一下Tarjan：

这里普及基本概念:

• 强连通分量：对于图G来说的一个子图中，任意两个点都可以彼此到达，这个子图就被称为图G的连通分量（一个点就是最小的连通分量）
• 时间戳：搜索到一个点时，这个点将被赋予一个 唯一 的时间量，并且越早搜到的点时间戳越小（当然了）

Tarjan是一个基于深搜，可以求解图中强连通分量的的算法，基本思想请看图：

在我们对一个图进行深度优先搜索时，走过的边会得到一棵搜索树，搜索树可以看做是原图抛弃了一些边而形成的

这便是一棵搜索树了

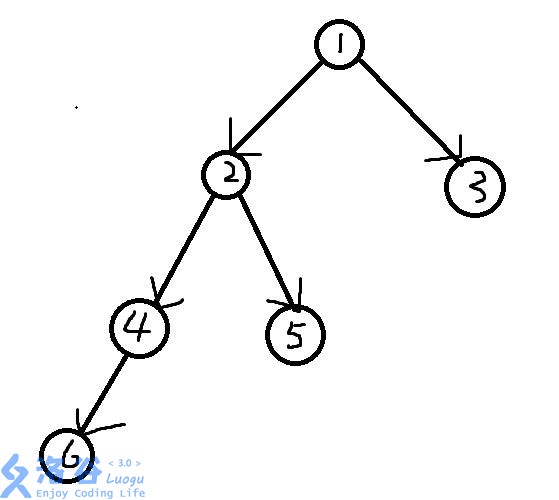
我们对抛弃掉的边做一个分类，对于这棵树中被还原的原图中的边有三种：

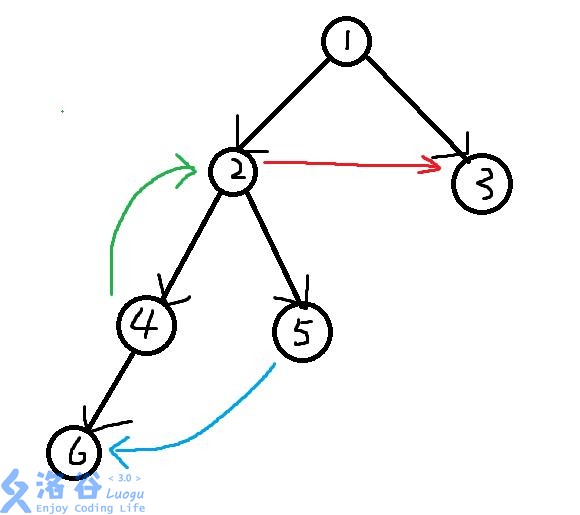
• 红色的边-横叉边
• 蓝色的边-前向边
• 绿色的边-后向边

不难发现，横叉边和前向边都无法构成回路，即不能形成大于一个点的强连通分量，所以我们要做的，就是找出重要的后向边来

怎么找后向边呢？你可以回想一下刚才提到的“时间戳”，没错，如果我们搜索到了一个之前搜过的点，且他当前点的祖先一样，那么毫无疑问的，我们走在了后向边上

Tarjan算法使用两个数组来维护这个信息：

• dfn[maxn]:储存每个点的时间戳
• low[maxn]:储存每个点访问祖先的能力

什么是访问祖先的能力呢？就是说，这个点最多能走回头路到什么地步，low数组储存的是他能访问到的最早祖先的dfn值，如果这个点没有回头路可走，那low值就是他自己的dfn值咯

好了，说了这么多，相信你已经有一些感觉了，我们来看Tarjan的模板代码：

struct edge{
	int x,y,w;
}E[maxm];
int dfn[maxn],low[maxn],tmmk=0;
bool v[maxn];//v数组用来跟踪这个点是否已经处理完毕，我们稍后会见到它的用法 
stack<int> S;
void tarjan(int x)
{
   dfn[x]=low[x]=++tmmk;//每个点在最开始被访问时，时间戳和low值都是一样的 
   S.push(x);
   v[x]=true;
   for(int i=head[x];i;i=next[i])//链式前向星查邻接点 
   {
     int y=E[i].y;//不熟悉的同学请像这样打多一点，有助于理解 
     if(!dfn[y])//dfn的初值都是0，如果这个点没有搜过，就递归搜索 
     {
       tarjan(y);
       low[x]=min(low[x],low[y]);//此时搜索已经回溯，我们可以确定y的low值已经更正，所以用它来更新x的 
     }//因为y在x的后面，所以y能访问到的祖先x一定可以访问到 
     else
       if(v[y])//如果y点搜过了且在栈里，说明我们找到了 后！向！边！ 
          low[x]=min(low[x],dfn[y]);
   }//但是此时我们还不能急着处理，为什么？因为有回溯到根了以后我们在收集到了完整的信息 
   if(dfn[x]==low[x])
   {//dfn和low一样，你就是与众不同的根节点 
      ans++;//ans是强连通分量的个数 
      int y;
      do{
        y=S.top();
        S.pop();
        v[y]=false;
        col[y]=ans;//y点属于编号为ans的强连通分量 
        g[ans].push_back(y);//存下每个强连通分量的成员
      }while(y!=x)//在这里将栈里的点全部倒出来（倒垃圾一样..） 
   }
}

回到题目！

题目要求求出图中最大强连通分量，和其中所有的点

我们可以看出，以上模板中col数组用不着了，存成员还是必要的，但是要求字典序输出，这个向量就不很方便了，我们可以用优先队列解决这个问题

关于优先队列的基本用法可以看我博客，这里关系不很大不做深究qwq

AC代码：不开O2 55ms（偷懒用stl的代价）开O2 35ms

#include<bits/stdc++.h>
using namespace std;

const int maxn=6000,maxm=110000;
int n,m;

int read(){
	int x=0;char c=getchar();
	while(c<'0' || c>'9')c=getchar();
	while(c>='0' && c<='9'){
		x=(x<<3)+(x<<1)+(c^'0');
		c=getchar();
	}
	return x;
}

int head[maxn],nxt[maxm],id=0;
struct edge{
	int x,y;
}G[maxm];
void add(int x,int y){
	G[++id].x=x;
	G[id].y=y;
	nxt[id]=head[x];
	head[x]=id;
}

struct pointer{//这是一个指针，p指向连通集编号，siz是他的大小方便排序
	int p,siz=0;
	int diction;//diction是第一个点的编号，如果严格字典序请改成数组
}p[maxn];

int dfn[maxn],low[maxn],col[maxn],
	tmmk=0,cnt=0;
stack<int> S;
priority_queue<int,vector<int>,greater<int> > g[maxn];
bool instk[maxn];
void tarjan(int x){
	dfn[x]=low[x]=++tmmk;
	S.push(x);
	instk[x]=true;
	for(int i=head[x];i;i=nxt[i]){
		int y=G[i].y;
		if(!dfn[y]){
			tarjan(y);
			low[x]=min(low[x],low[y]);
		}
		else if(instk[y])
			low[x]=min(low[x],dfn[y]);
	}
	if(dfn[x]==low[x]){
		cnt++;
		int y;
		p[cnt].diction=S.top();
		do{
			y=S.top();
			S.pop();
			instk[y]=false;
			col[y]=cnt;
			p[cnt].p=cnt;
			p[cnt].siz++;
			g[cnt].push(y);
		}while(y!=x);
	}
}

bool cmp(pointer a,pointer b){
	if(a.siz!=b.siz)
		return a.siz>b.siz;
	else
		return a.diction<b.diction;
}

int main(){
	n=read(),m=read();
	
	int x,y,f;
	for(int i=1;i<=m;i++){
		x=read(),y=read(),f=read();
		add(x,y);
		if(f==2)
			add(y,x);
	}
	
	memset(dfn,0,sizeof(dfn));
	memset(instk,false,sizeof(instk)); 
	for(int i=1;i<=n;i++)
		if(!dfn[i])
			tarjan(i);
	
	sort(p+1,p+cnt+1,cmp);
	
	printf("%d\n",p[1].siz);
	while(!g[p[1].p].empty()){
		printf("%d ",g[p[1].p].top());
		g[p[1].p].pop();
	}
		
	return 0;
}

PS：本题数据略水，题解中有些并没有考虑到一般字典序还A掉的，希望同学们注意。另：我这样做也只考虑第一个数的字典序，如果严格排列把字典diction改成数组即可

PSPS：大半夜写这个挺累的，如果有帮到你，请不要吝惜你的赞（笑）