自动搬运

查看原文

来自洛谷，原作者为

	EternalAlexander 魔力的碎片都不再拥有的少年

搬运于2025-08-24 21:28:13，当前版本为作者最后更新于2020-12-15 18:49:26，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

之前的 dfs 剪枝全是假的，10 0 没有一个跑得出来。

计算最短路是容易的，考虑计算最长路。可令 $dp_{i,j,S}$ 表示考虑到格子 $(i,j)$，轮廓线上的插头方案为 $S$ 时的最长路径。

考虑 $S$ 需要记录哪些信息，发现只需要维护插头之间的连通性，使合并插头的时候不连出环即可。也就是我们可以用一个长为 $n+1$ 的数组 $A$ 表示 $S$，$A_i = 0$ 表示当前位置没有插头，$A_i = 1$ 表示当前插头和源点联通，否则如果 $A_i > 1$，$A_i = A_j$ 表示插头 $i$ 和 $j$ 联通。采用最小表示法即可使 $S$ 对应的 $A$ 唯一。

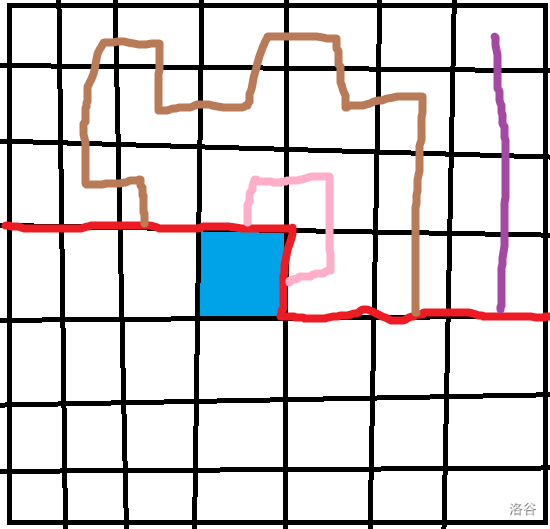
上图轮廓线的状态对应的 $A = [0,0,2,3,3,0,2,1]$

考虑 $S$ 的可能状态数，发现：

1.对于 $x > 1$，只可能存在 $0$ 个或者 $2$ 个 $i$ 满足 $A_i = x$.

2.不存在 $i < j < k < l$ 且 $A_i = A_k$, $A_j = A_l$

也即 $A_i > 1$ 的位置一定可以表示为一个合法的括号序列，那么可以得到状态数是低于 $3^n$ 的。事实上状态数是低于这个界的。因此以上算法的时间复杂度为 $O(n^c 3^n )$，其中 $c$ 为一取决于实现方式的常数。

（下面的代码需要 C++11）

#include <bits/stdc++.h>

using pii = std::pair<int,int>;
const int inf = 1e7;

int dx[] = {0,1,0,-1};
int dy[] = {1,0,-1,0};

int n,m,dis[12][12],ban[12][12];

std::map< std::vector<int> , int >dp[12][12];	

std::vector<int> process(std::vector<int>S) {
	int cnt = 1;
	int vis[30] = {0};
	for (int i = 1; i <= n + 1; ++ i) {
		if (S[i] == 0 || S[i] == 1) continue;
		if (!vis[S[i]]) { vis[S[i]] = ++cnt; S[i] = cnt; }
		else S[i] = vis[S[i]];
	} return S;
}
std::vector<int> shift(std::vector<int>S){ for (int i = 1; i <= n; ++ i) S[i] = S[i+1]; S[n+1] = 0; return S; }
std::vector<int> trans(std::vector<int>S,int i) { std::swap(S[i],S[i+1]); return S; }
std::vector<int> create(std::vector<int>S,int i) { S[i] = S[i+1] = 20; return process(S); }
std::vector<int> merge(std::vector<int>S,int i) {
	int p = S[i], q = S[i+1], flag = 20;
	if (p == 1 || q == 1) flag = 1;
	for (int i = 1; i <= n + 1; ++ i) if (S[i] == p || S[i] == q) S[i] = flag;
	S[i] = S[i+1] = 0;
	return process(S);
}

int main() {
	
	scanf("%d%d",&n,&m);
	for (int i = 1; i <= m; ++ i) {
		int x,y;
		scanf("%d%d",&x,&y);
		ban[x][y] = 1;
		assert( not ( (x == 1 && y == n)  or (x == n && y == 1) ) );
	}
	
	auto bfs = [&]() {
		std::memset(dis,-1,sizeof(dis));
		std::queue< pii >q;
		q.push( { 1,n } );
		dis[1][n] = 0;
		while (q.size()) {
			auto u = q.front(); q.pop();
			int x = u.first, y = u.second;
			for (int i = 0; i < 4; ++ i) {
				int x1 = x + dx[i], y1 = y + dy[i];
				if (x1 < 1 || x1 > n || y1 < 1 || y1 > n || dis[x1][y1] != -1 || ban[x1][y1]) continue;
				dis[x1][y1] = dis[x][y] + 1;
				q.push( { x1,y1 } );
			}
		} 
	};  bfs();
	
	std::vector<int>v(n+2);
	v[n+1] = 1; dp[1][n-1][v] = 1;
	v[n+1] = 0; v[n] = 1; dp[1][n-1][v] = 1;
	
	for (int i = 1; i <= n; ++ i) {
		for (int j = n - (i == 1); j >= 1; j --) {
			for (auto P:dp[i][j]) {
				auto S = P.first; int v = P.second;
				int p = S[j], q = S[j+1];
				if (p == 0 && q == 0) dp[i][j-1][S] = std::max(dp[i][j-1][S],v);
				if (ban[i][j]) continue;
				if (p == 0 && q == 0) {
					auto T = create(S,j);
					dp[i][j-1][T] = std::max(dp[i][j-1][T],v + 1);
				}
				if ((p != 0) + (q != 0) == 1) {
					dp[i][j-1][S] = std::max(dp[i][j-1][S],v + 1);
					auto T = trans(S,j);
					dp[i][j-1][T] = std::max(dp[i][j-1][T],v + 1);
				}
				if (p && q && p != q) {
					auto T = merge(S,j);
					dp[i][j-1][T] = std::max(dp[i][j-1][T],v + 1);
				}
			}
		} for (auto P:dp[i][0]) {
			auto S = P.first; int v = P.second;
			if (S[1] == 0) dp[i+1][n][shift(S)] = dp[i][0][S];
		}
	}
	std::vector<int>S1(n+2),S2(n+2);
	S1[1] = 1; S2[2] = 1;
	printf("%d",std::max(dp[n][1][S1],dp[n][1][S2]) - dis[n][1]);
	return 0;
}