自动搬运

查看原文

来自洛谷，原作者为

	cly312 忍一时风平浪静，退一步人财两空

搬运于2025-08-24 21:28:05，当前版本为作者最后更新于2024-08-01 23:32:36，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

这题的关键就在于能否将问题转化成集合之间是否有交集。

首先，考虑一个我们无法形成进化树的例子，例如这样：

3
1 fly
1 man
2 fly man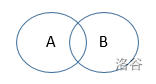

如果我们想根据这个输入构建一棵树，我们需要在根上分割 A 或 B，但剩下的两个子树都需要有一条边来添加另一个特征。显然输出为"No"。

如果我们输入中的特征 A 和 B 中的任何两个表示如上所述的交集不为空，那么我们就无法构建一棵合适的树。

像下面的例子就可以用一棵树来表示：

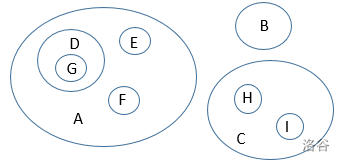
画出来的树长这样：

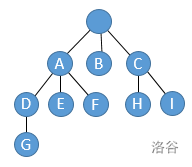
相信你已经理解了我们只需要判断是否任意两个集合中交集是否为空就可以了，代码：

#include<bits/stdc++.h>
using namespace std;

int N;
vector<string> c[25];
vector<string> allc;

//集合是否相交 
bool crossing(int a, int b) {
	int A=0, B=0, AB=0;
	for (int i=0; i<N; i++) {
		vector<string> &v = c[i];
		bool has_a = false, has_b = false;
		for (int j=0; j<v.size(); j++) {
			if (v[j]==allc[a]) has_a = true;
			if (v[j]==allc[b]) has_b = true;
		}
		if (has_a && has_b) AB++;
		else if (has_a) A++;
		else if (has_b) B++;
	}
	return AB>0 && A>0 && B>0;
}

int main() {
	cin >> N;
	string s;
	for (int i=0; i<N; i++) {
		int K;
		cin >> K;
		for (int j=0; j<K; j++) {
			cin >> s;
			c[i].push_back(s);
			bool found = false;
			for (int k=0; k<allc.size(); k++)
				if (allc[k] == s) found = true;
			if (!found) allc.push_back(s);
		}
	}
	int M = allc.size();
	bool ok = true;
	for (int a=0; a<M; a++)
		for (int b=a+1; b<M; b++)
			if (crossing(a, b)) ok = false;
	if (ok) cout << "yes\n";
	else cout << "no\n";
	return 0;
}