自动搬运

查看原文

来自洛谷，原作者为

	Manjusaka丶梦寒 **

搬运于2025-08-24 21:27:40，当前版本为作者最后更新于2018-09-20 19:55:28，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

只能说这是一道数学题，似乎并没有蓝题那么难。

当我们第一眼度完题的时候，很显然我们要找到所有直线相交的最高点。

幸运的是$n \le 5000$,我们计算出每一条直线的解析式来以后$n^2$枚举就好了，题解中也有这种做法的解答，就不详细说了，我们考虑要是数据再大一点呢？ 我们考虑二分答案，毕竟$n \times n$和$n \times logn$那完全就是两个概念啊。

求直线的解析式应该初中就学了吧，为了避免某些人没学还是稍微提一下吧(大佬可直接跳过)。

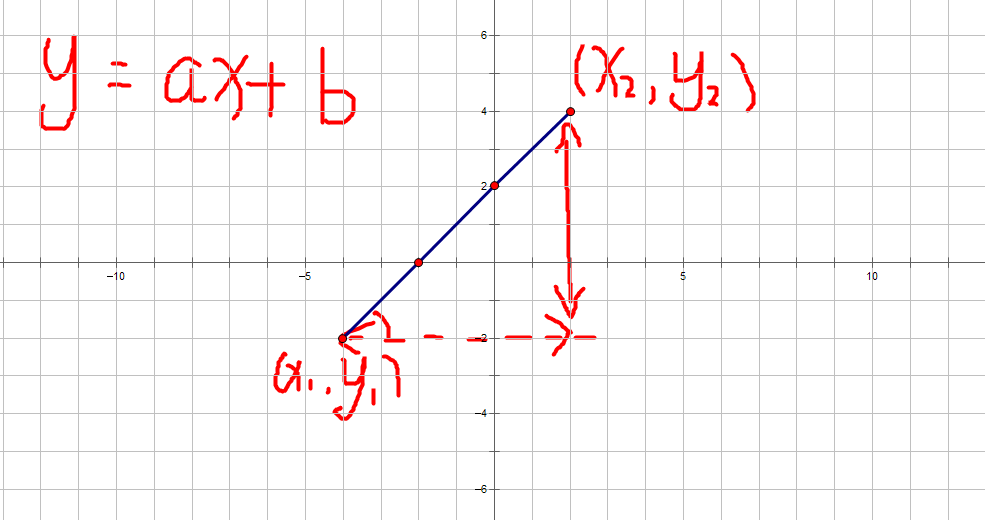
对于这直线来说，首先第一==定义函数解析式为$y=ax+b$ 斜率$a$，为$(y1-y2)/(x1-x2)$,有了斜率我们要求b的值，我们将斜率带入直线上某个点带入$(x_1,y_1)$，那么$$y=ax+b=>y_1=ax_1+b=>b=y_1-ax_1$$ 这就求出了一条直线函数解析式。 接下来我们就可以枚举答案了，高度左边缘为$0$,右边缘最大为$1000000$.

最重要的就是$check()$函数啦。 对于每个函数值得判断我们要确定这条直线在哪个区间范围内满足可以被看见(函数值小于判断的值)。 还是看图吧，假设现在判断答案c是否合法。 对于斜率小于0的直线来说

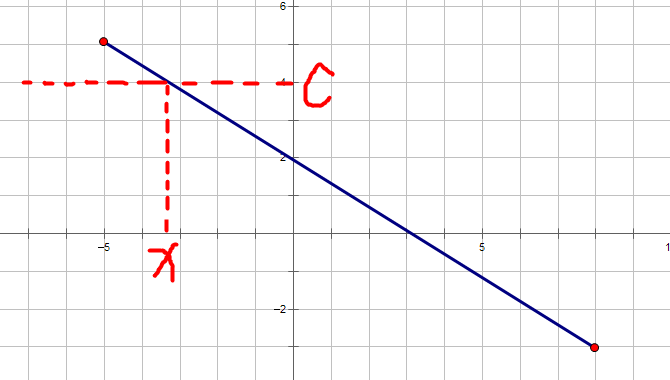
我们找到$y=c$这条直线与直线的交点$x$，那么对于任意大于$x$的点都是看一由$c$照亮的，那么我们对于斜率小于0的每一条直线记录一个合法的最大左边界$L$(因为要满足所有直线)。

同理对于斜率大于0的直线，求一个最小的右端点$R$。

对于斜率等于0的直线只需要判断b是否小于c就好了。 当$L \le R$是答案合理。

#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <queue>
#include <cmath>
using namespace std;
int n;
double x[5006],y[5006],a[5006],b[5006],ans;
bool check(double x)
{
	double L=-2e9,R=2e9;
	for(int i=2;i<=n;i++)
	{
		if(a[i]<0)L=max(L,(x-b[i])/a[i]);
		else if(a[i]>0)R=min(R,(x-b[i])/a[i]);
		else if(x<b[i])return 0;
	}
	return L<=R;
}
int main()
{
	scanf("%d%lf%lf",&n,&x[1],&y[1]);
	for(int i=2;i<=n;i++)
	{
		scanf("%lf%lf",&x[i],&y[i]);
		a[i]=(y[i]-y[i-1])/(x[i]-x[i-1]);
		b[i]=y[i]-a[i]*x[i];
	}
	double l=0,r=1000000;
	while(l<=r)
	{
		double mid=(l+r)/2;
		if(check(mid))r=mid-0.0001,ans=mid;
		else l=mid+0.0001;
	}
	printf("%.2lf",ans);
}

鄙人不才，有错误请指出，喜欢就点个赞吧。