自动搬运

查看原文

来自洛谷，原作者为

	隐心 此处是坑，抬头望天

搬运于2025-08-24 21:27:30，当前版本为作者最后更新于2018-09-21 09:39:48，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

这道题要求求的是曼哈顿距离，什么是曼哈顿距离呢？题目里已经解释了，几个点之间的横纵坐标的差的绝对值，所以这里我们以二维的图为例子。

您好，您的灵魂画手已上线

就二维的图来说，存在两种情况

不会上传本地的画图那就用表格代替了，假装这是一个平面直角坐标器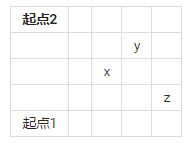

怎么调表格都不对仗工整那就这样吧

我这里举出了二维中的所有情况，x与y这种的左边的在下面，和x与z这种的左边的在上面。

对于x与y之间的曼哈顿距离，是不是等于y到起点1的曼哈顿距离减去x到起点1的曼哈顿距离？

对于x与z之间的曼哈顿距离，是不是等于z到起点2的曼哈顿距离减去x到起点2的曼哈顿距离？

所以我们就可以算出来距离起点1最小的曼哈顿距离和距离起点1最大的曼哈顿距离之间的差，然后将这个同距离起点2最小的曼哈顿距离和距离起点2最大的曼哈顿距离之间的差相比较，取最大值。

这样即为二维的解。所以以此类推，在三维状态下，有四种情况，在四维状态下，作为一个三维生物，我是真的想象不出来有几种，我姑且猜想有八种情况~~（虽然我只考虑四种情况也过了，可能是数据正好吧）~~，但是严谨一点来说，枚举所以第四维的情况的话是有八种的。这点欢迎大佬留言讨论一下。

所以代码如下

#include<bits/stdc++.h>
#define ll long long
ll start=0x7fffffff;
using namespace std;
ll read(){
	ll x=0,f=1; char c=getchar();
	while(c<'0'||c>'9'){if(c=='-')f=-1; c=getchar();}
	while(c>='0'&&c<='9'){x=x*10+c-'0'; c=getchar();}
	return x*f;
}
ll x[]={-start,-start,-start,-start,-start,-start,-start,-start};
ll y[]={-start,start,start,-start,-start,start,start,-start};
ll z[]={-start,-start,start,start,-start,-start,start,start};
ll ls[]={-start,-start,-start,-start,start,start,start,start};
ll a[10];
ll sum[10];
ll maxx[10];
ll minn[10];
ll ans;
ll n,d;
int main()
{
	cin>>n>>d;
/*	if(d==4)
	{
		//cout<<"我想象不出四维";
		return 0;
	}*/
	for(ll i=1;i<=n;i++)
	{
		for(ll j=1;j<=d;j++)
		{
			a[j]=read();//用cin直接超时，不要问我怎么知道的
		}
		for(ll j=0;j<8;j++)
		{
			sum[j]=0;
		}
		for(ll j=0;j<8;j++)
		{
			sum[j]=sum[j]+abs(a[1]-x[j])+abs(a[2]-y[j])+abs(a[3]-z[j])+abs(a[4]-ls[j]);
		}
		for(ll j=0;j<8;j++)
		{
			if(sum[j]>maxx[j])
			{
				maxx[j]=sum[j];
			}
			if(sum[j]<minn[j]||minn[j]==0)
			{
				minn[j]=sum[j];
			}
			if(ans<maxx[j]-minn[j])
			{
				ans=maxx[j]-minn[j];
			}
		}
	}
	cout<<ans;
	return 0;
}

以及在线求大佬给估一下时间复杂度