自动搬运

查看原文

来自洛谷，原作者为

	WKAHPM 这个家伙很菜，什么也没有留下

搬运于2025-08-24 21:26:41，当前版本为作者最后更新于2019-10-08 22:24:19，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

0.问题类型

这是一道经典的最大子矩形问题，本人的思路参考了国家队wzk大佬的论文《浅谈用极大化思想解决最大子矩形问题》

这篇论文介绍了两种求最大子矩形的思路，分别是通过障碍点找子矩形和通过悬线找子矩形，本题的数据范围适合使用第一种方法

1.算法思路

定义极大子矩形为$4$条边都不能向外拓展的有效子矩形（这里的有效即子矩形内不包括障碍点)。

可以得到最大子矩形是所有极大子矩形中最大的，所以只要枚举最大的子矩形，求出其中最大的即可

2.算法实现

怎么找极大子矩形？根据极大子矩形的定义，我们可以得出极大子矩形的$4$条边一定覆盖障碍点（或边界）

为了方便讨论，我们先将整个牛场的4个顶点设为障碍点。

例如

10 10

4

1 1

3 4

6 3

9 8

1.从左往右搜

将障碍点按横坐标排序（左右顺序）后得到如下编号。

(作者画画不是那么好qwq)

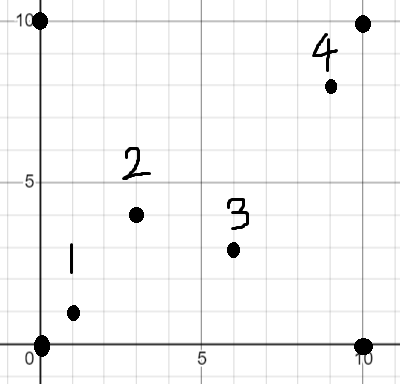
一开始从$1$号障碍点开始，从左往右找极大子矩形。

一开始的极大子矩形上下边界$up,low$为整个牛场的上下边界

$1$号障碍点往右找，到$2$号障碍点，如图

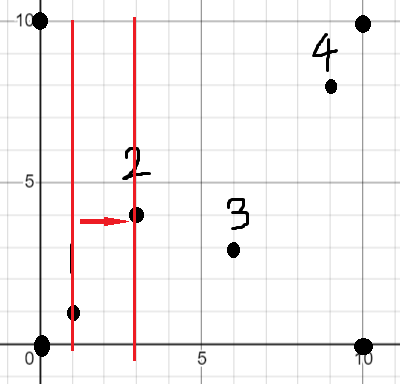
可以得到一个极大子矩形，它的面积就是障碍点$2$的横坐标减去障碍点$1$的横坐标乘以上边界减去下边界。

接下来需要对上下边界做一些修改，否则之后的极大子矩形可能会包括障碍点。因为$2$的纵坐标大于$1$的纵坐标，所以修改上边界，修改为$2$的纵坐标。

接下来到$3$，同理可以得到如下极大子矩形

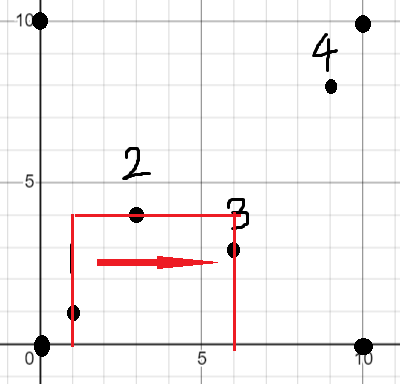
它的面积就是$3$的横坐标减去$1$的横坐标乘以上边界（$2$的纵坐标）减去下边界

之后的$4$也同理。

然后从$2$开始往右找，从$3$开始往右找,从$4$开始往右找，跟从$1$开始找都是一样的。

2.从右往左搜

从左往右搜后我们会发现有一些遗漏的情况，就是极大子矩形的左边界是牛场的左边界，右边界覆盖一个障碍点的情况，如图

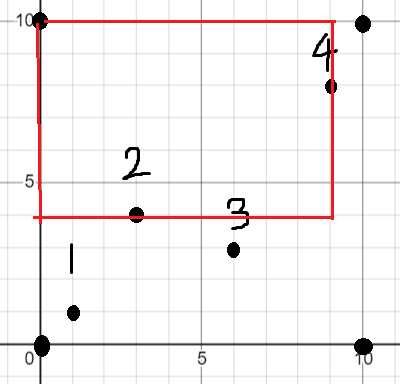
解决方法很简单，把从左往右搜倒过来从右往左搜一遍即可

3.特殊情况

在从左往右搜和从右往左搜后我们发现还有一种情况没有考虑到，就是极大子矩形的左右边界分别是牛场的左右边界，如图

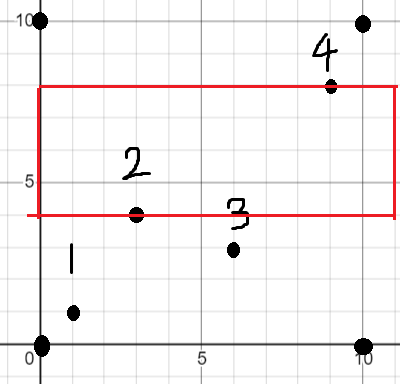
解决方法是，再将障碍点按纵坐标排序，如图

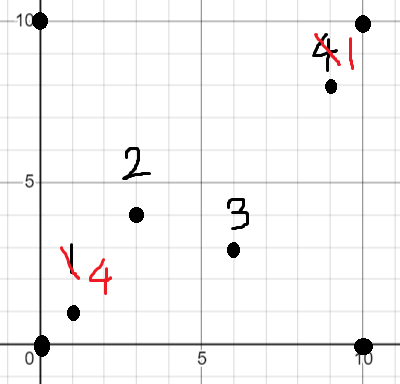
可以得到这类极大子矩形的面积就是相邻两个障碍点（按纵坐标排序后）纵坐标之差乘以牛场的长

时间复杂度$O(N^2)$，$N$为障碍点数

3.代码实现

#include<bits/stdc++.h>
using namespace std;

int read()//快读
{
	int sum = 0 , f = 1;
	char c = getchar();
	while(c < '0' or c > '9')
	{
		if(c == '-') f = -1;
		c = getchar();
	}
	while(c >= '0' and c <= '9')
	{
		sum = (sum << 1) + (sum << 3) + c - '0';
		c = getchar();
	}
	return sum * f;
}

struct S{//存放障碍点信息
	int x , y;
}s[5010];

bool cmp1(S a , S b)//按横坐标排序
{
	if(a.x != b.x) return a.x < b.x;
	else return a.y < b.y; 
}

bool cmp2(S a , S b)//按纵坐标排序
{
	if(a.y != b.y) return a.y < b.y;
	else return a.x < b.x ; 
}

int l , w , n , ans; 

int main()
{
    l = read() , w = read() , n = read();   
    for(int i = 1; i <= n; i ++) s[i].x = read() , s[i].y = read();
    s[++ n].x = 0 , s[n].y = 0;//将四个顶点设为障碍点
	s[++ n].x = 0 , s[n].y = w;
	s[++ n].x = l , s[n].y = 0;
	s[++ n].x = l , s[n].y = w;
    int x1 , x2 , y1 , y2;//x1为左边界，x2为右边界,y1为下边界，y2为上边界
    //从左往右搜
    sort(s + 1 , s + n + 1 , cmp1);
    for(int i = 1; i <= n; i ++)
    {
    	x1 = s[i].x , y1 = 0 , y2 = w;
    	for(int j = i + 1; j <= n; j ++)
    	{
				x2 = s[j].x;
				ans = max(ans , (x2 - x1) * (y2 - y1));
	    		if(s[j].y < s[i].y) y1 = max(y1 , s[j].y);//更新上下边界
	    	    else y2 = min(y2 , s[j].y); 
		}
	}
    //从右往左搜  
    for(int i = n; i >= 1; i --)
    {
    	x1 = s[i].x , y1 = 0 , y2 = w;
    	for(int j = i - 1; j >= 1; j --)
    	{
	    		x2 = s[j].x;
				ans = max(ans , (x1 - x2) * (y2 - y1));
				if(s[j].y < s[i].y) y1 = max(y1 , s[j].y);
	    	    else y2 = min(y2 , s[j].y); 
		}
	}

	//处理特殊情况
	sort(s + 1 , s + n + 1 , cmp2); 
	for(int i = 1; i <= n - 1; i ++)
	{
		ans = max(ans , l * (s[i + 1].y - s[i].y));
	}
	
	printf("%d" , ans);
	return 0;
}