自动搬运

查看原文

来自洛谷，原作者为

	Diaоsi Enemy of God

搬运于2025-08-24 21:25:48，当前版本为作者最后更新于2020-04-30 15:52:50，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

窗口的星星

题意不再过多赘述，首先我们思考一个问题，就是在什么条件下星星才会出现在窗户中。

设某颗星星的坐标为 $(x,y)$ ，则当窗户的右上角端点的坐标出现在 $(x\sim x+w-1,y\sim y+h-1)$ 这个范围内时，星星就会出现在窗户里。

如下图：

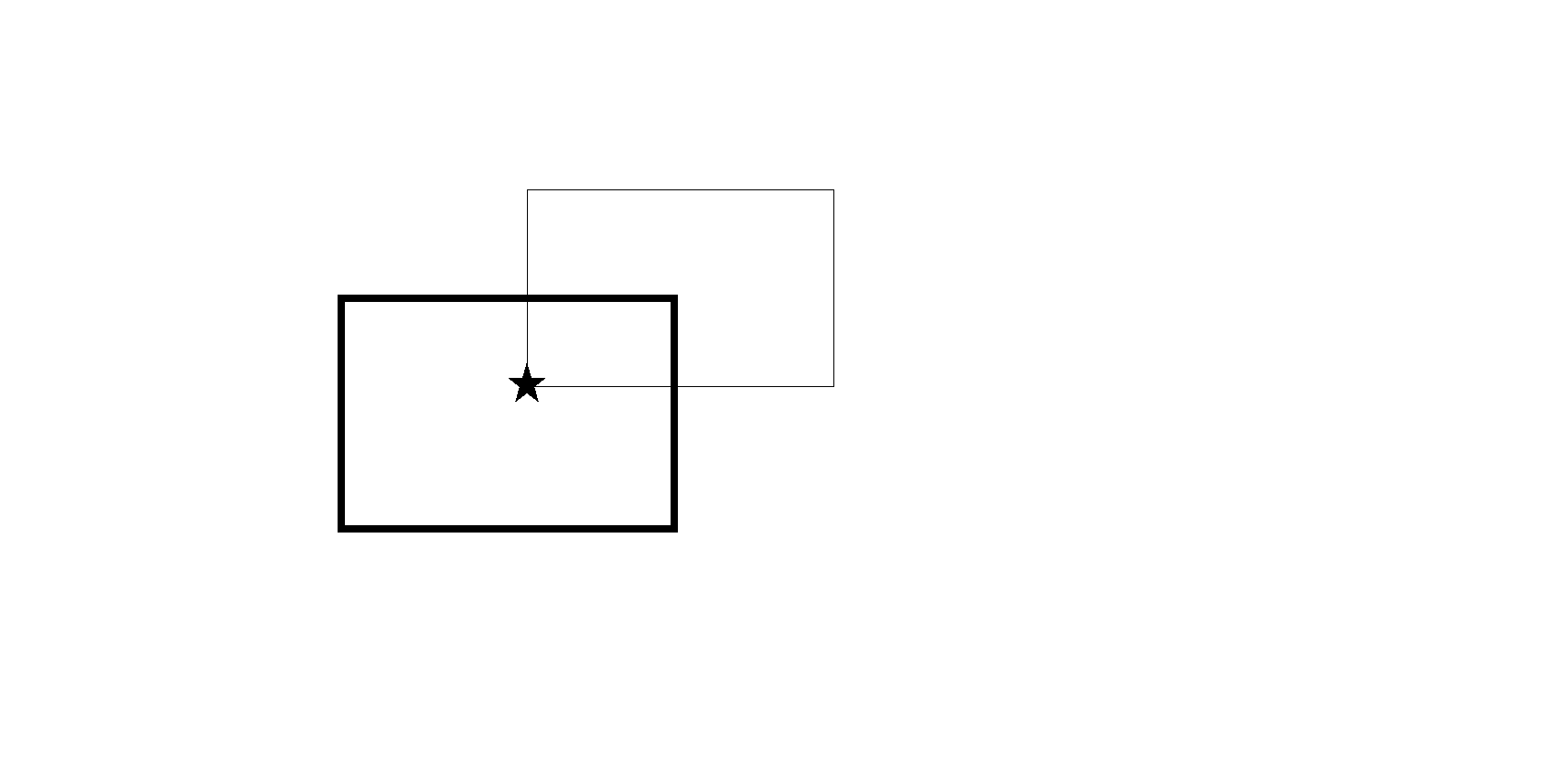
因为题目中说出现在窗户边框的星星不算，我们不妨将边框长宽都减小 $0.5$ ，所以边界坐标要 $-1$ ，即 $(x+w-1,y+h-1)$ 。

于是我们可以将每个星星都扩展成一个矩形，这时我们注意到，若两个矩形之间有交集，他们便可以放在同一个窗户中。

如下图：

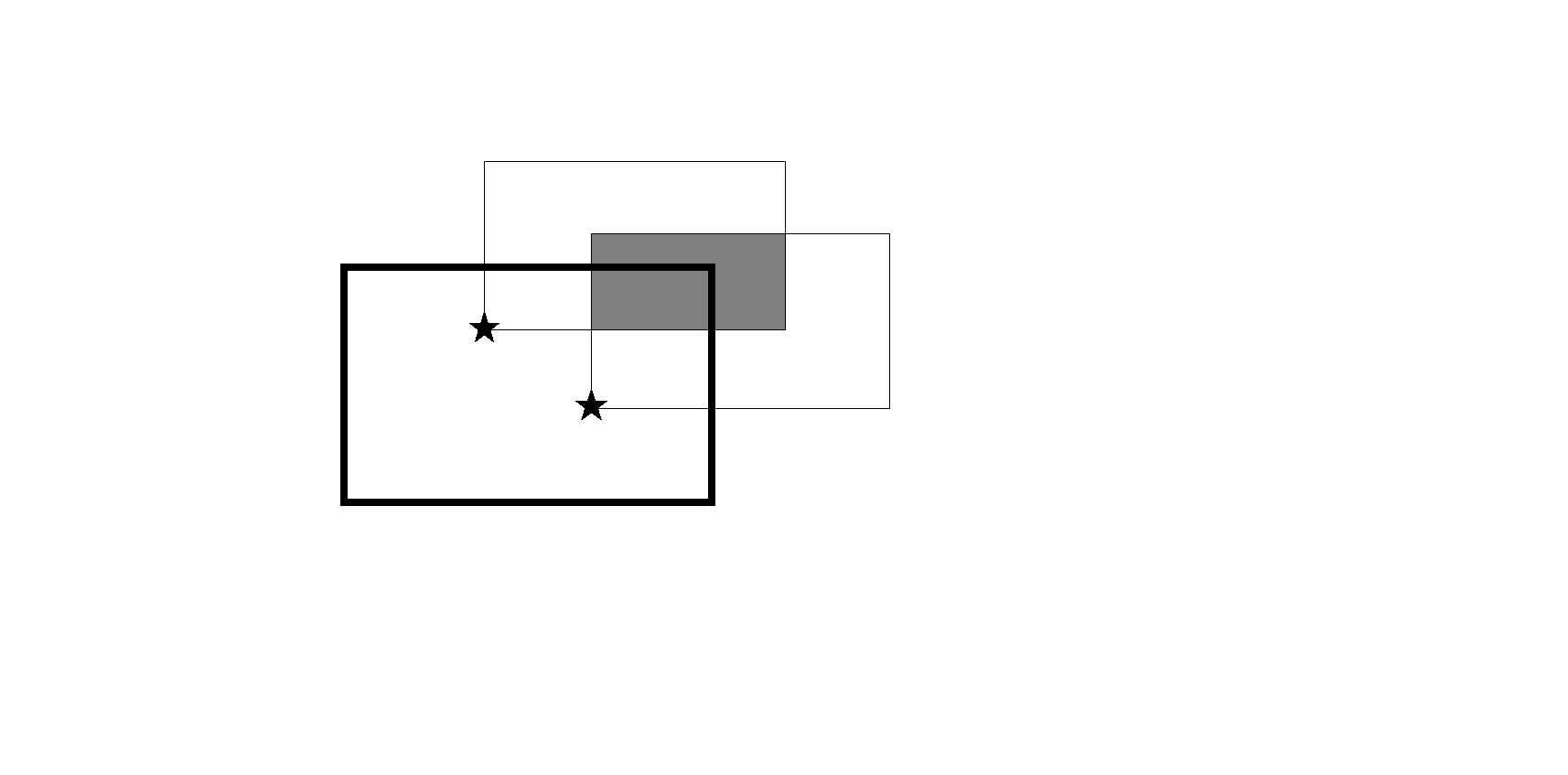
图中灰色的部分就是两个星星构成的矩形的交集，只要窗户的右上角端点在灰色区域内，就能同时框住两个星星。

此时我们可以将问题转化为：平面上有若干个矩形，每个矩形都带有一个权值，求在哪个坐标上权值的总和最大。

接下来我们就可以使用扫描线来解决这个问题了，若当前星星的亮度值为 $l$ ,则矩形的入边的权值设为 $l$ ，出边为 $-l$ ，此时我们只要求扫描线上的区间最大值即可得出答案，区间查询可以使用 lazy_tag 的方式实现。

代码实现上的一些小细节：

• 在对 $x$ 坐标进行升序排序时，将 $val$ 值按降序排序，这样才能处理两个矩形贴合的情况。
• 观察到 $0 \leq x_i,y_i \leq 2^{31}$ 所以我们需要将坐标进行离散化处理。

既然你能找到这题，我相信你能瞬间做出来的。

Code:

#include<bits/stdc++.h>
typedef long long LL;
typedef long double LD;
using namespace std;//你在看我的代码对吧 
const LL N=100010;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x<y?x:y;}
inline void swap(int &x,int &y){x^=y^=x^=y;}
LL T,n,w,h,C[N];
struct Segment{
	LL l,r,h;
	LL val;
	bool operator <(const Segment &a)const{
		return (h!=a.h)?h<a.h:val>a.val;
	}
}Seg[N<<2];
struct SegmentTree{
	LL l,r;
	LL mx,add;
	#define l(x) tree[x].l
	#define r(x) tree[x].r
	#define mx(x) tree[x].mx
	#define add(x) tree[x].add
}tree[N<<2];
void init(){
	memset(Seg,0,sizeof(Seg));
	memset(tree,0,sizeof(tree));
}
void Pushup(LL x){
	mx(x)=max(mx(x<<1),mx(x<<1|1));
}
void Build(LL x,LL l,LL r){
	l(x)=l,r(x)=r,mx(x)=add(x)=0;
	if(l==r)return;
	LL mid=(l+r)>>1;
	Build(x<<1,l,mid);
	Build(x<<1|1,mid+1,r);
}
void Pushdown(LL x){
	mx(x<<1)+=add(x);
	mx(x<<1|1)+=add(x);
	add(x<<1)+=add(x);
	add(x<<1|1)+=add(x);
	add(x)=0;
}
void Change(LL x,LL L,LL R,LL d){
	LL l=l(x),r=r(x);
	if(L<=l&&r<=R){
		mx(x)+=d;
		add(x)+=d;
		return;
	}
	Pushdown(x);
	LL mid=(l+r)>>1;
	if(L<=mid)Change(x<<1,L,R,d);
	if(R>mid)Change(x<<1|1,L,R,d);
	Pushup(x);
}
int main(){
	scanf("%lld",&T);
	while(T--){
		init();
		scanf("%lld%lld%lld",&n,&w,&h);
		for(LL i=1;i<=n;i++){
			LL x,y,l;
			scanf("%lld%lld%lld",&x,&y,&l);
			C[(i<<1)-1]=y;
			C[i<<1]=y+h-1;
			Seg[(i<<1)-1]=(Segment){y,y+h-1,x,l};
			Seg[i<<1]=(Segment){y,y+h-1,x+w-1,-l};
		}
		n<<=1;
		sort(C+1,C+n+1);
		sort(Seg+1,Seg+n+1);
		LL cnt=unique(C+1,C+n+1)-C-1;
		for(LL i=1;i<=n;i++){
			LL pos1=lower_bound(C+1,C+cnt+1,Seg[i].l)-C;
			LL pos2=lower_bound(C+1,C+cnt+1,Seg[i].r)-C;
			Seg[i].l=pos1;
			Seg[i].r=pos2;
		}
		Build(1,1,cnt);
		LL ans=0;
		for(LL i=1;i<=n;i++){
			Change(1,Seg[i].l,Seg[i].r,Seg[i].val);
			ans=max(ans,mx(1));
		}
		printf("%lld\n",ans);
	}
	return 0;
}