自动搬运

查看原文

来自洛谷，原作者为

	Creroity 欸嘿

搬运于2025-08-24 21:25:45，当前版本为作者最后更新于2020-08-05 22:52:23，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

啊，又一道可以打题解的题！我已经跃跃欲试了呢！

咳咳，回归正题。

像这种题目，我们可以画一下图。

当然，这题也有两个步骤，先要考虑放置的方法数：（我们拿样例来举个例子）

先是画一个边长为4的正方形格子，这个应该不用我多说。

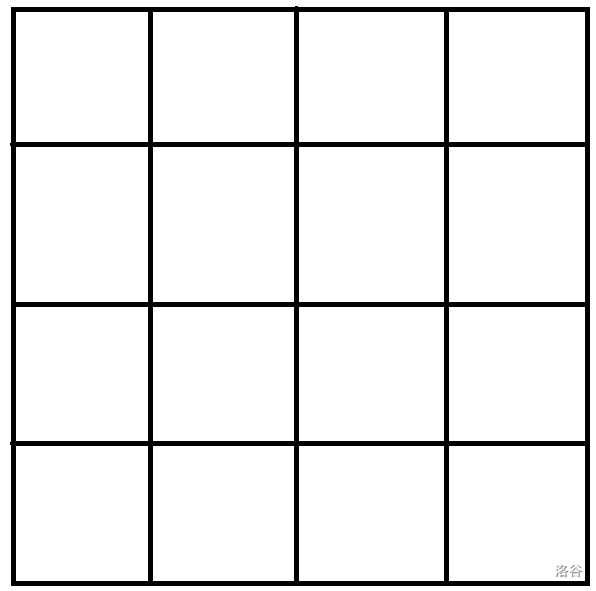
然后是第一个木牛流马：

从图上不难看出这里每个格子都是可以放的，共有 $4\times 4$ 种可能。

（这里就先随便放一个位置了）

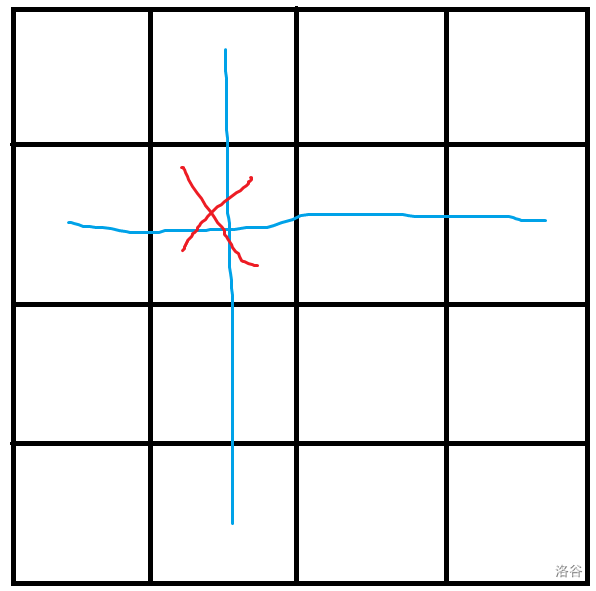
红色的叉叉代表木牛流马的位置，但是题目中说：

可是在现实中它有个缺陷，就是两个不能在同一行或同一列！

所以，放置过木牛流马的同一行同一列需要标记去掉。（图中的蓝色线表示删除）

接着，我们也不难发现剩下来可以放的位置刚好少了一行、一列。

所以剩下的位置放置方法数 $ans=(4-1) \times (4-1)$ 。

再放第二个木牛流马：

（也先随意放一个位置）

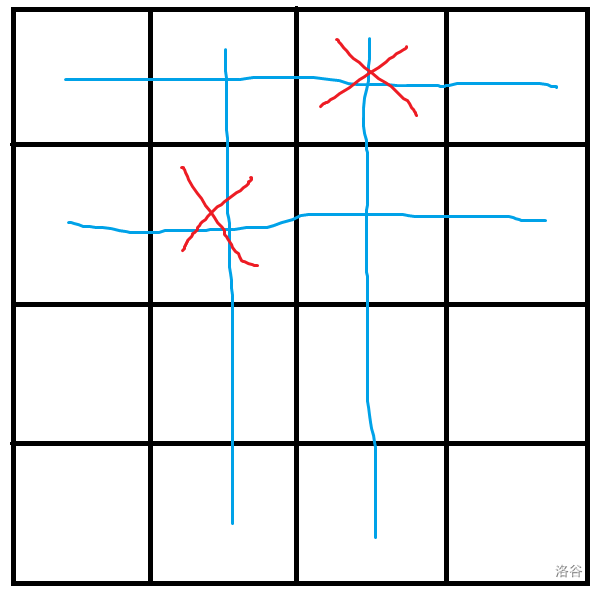
欸？接下来的位置刚好又是少了一行、一列呢！

所以，到这儿，我们应该可以找到规律了。

---

对，所以可以得出木牛流马的放置方法数 $ ans=n^2 \times (n-1)^2 \times (n-2)^2 \times \ldots \times (n-k+1)^2 $

---

接着再看颜色的影响：

我们还是拿样例举例子。

假设我们是这么放木牛流马的：

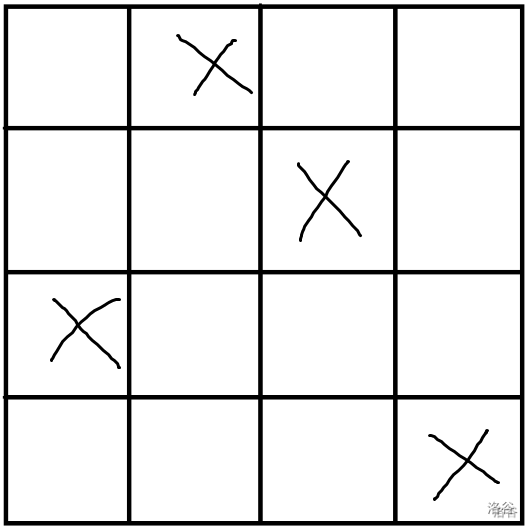
但是按照一开始假设的来讲，这里的任何一个都可以是第一个放的。

也就是说，这里的所有颜色都被我们假设成了不一样的。

所以我们还得要将颜色造成的多出来的方法数去掉。

首先，我们算出这种方法在颜色全都不同时的可能性共有几种。

很容易算出，共有 $4 \times 3 \times 2 \times 1$ 种也就是 $4!$ 种可能性。

但是因为颜色数等于4，所以实际上只有一种方法。那么它就使答案多了 $4!$ 种方法数。

那我们再假设，此时 $h=2$ ，第一种颜色个数是1，第二种颜色个数是3。

考虑第一种颜色，共一个，所以假设剩下的颜色还是都不相同的，那么可能性就变成了 $4 \times 3 \times 2$ 个，也就是 $4! \div 1$ 。

再考虑第二种颜色，是三个，那么可能性又变成了4个，也就是 $4! \div 3!$ 个。

---

那么我们又可以得出结论了，每一种颜色，都会造成答案多出 $C_i$ 种可能性，那么我们只用把答案除以 $C_1! \cdot C_2! \cdot \ldots \cdot C_h!$ 就可以得出正确答案了。

---

啊，那么终于到了上代码的时间了！

（因为前面讲得比较清楚，所以代码里有一些注释就没有加）

来！咱们上代码！！！

#include<bits/stdc++.h>
using namespace std;
int n,k,h;
long long ans=1,c;//十年OI一场空，不开long long见祖宗 
int main(){
	cin>>n>>k>>h;
	//有人说这里要加一个特判，但其实不需要，因为当k>n时，后面的（n-i+1）就会有一个变成0，那么答案就一定是0了 
	for(int i=1;i<=k;i++){
		ans*=(n-i+1)*(n-i+1);  
	}
	for(int i=1;i<=h;i++){
		cin>>c;
		for(int j=1;j<=c;j++)ans/=j;
	}
	cout<<ans;
	return 0;//记得养成好习惯 
}