自动搬运

查看原文

来自洛谷，原作者为

	diamond_153 这个人很勤快，写好了又删了

搬运于2025-08-24 21:25:11，当前版本为作者最后更新于2023-03-24 13:16:13，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

P1448 [NOI1998] 围巾裁剪 题解

看到这个题面，大家应该可以想到 $dp$。

我们先用 $a[i][j]$ 存储点 $(i,j)$ 是否被蛀虫咬坏，是为 $0$，不是为 $1$。

下一步我们设 $a[i][j](2\nmid j)$ 表示从点 $(i,j)$ 开始，最多可以向下延伸出一个没有任何小三角形被蛀虫咬坏，边长为 $a[i][j]$ 的正三角形。我们可以得到：

$$a[i][j]=\begin{cases} 0 &(a[i][j]\text{的原值为}0)\\ 1 &(a[i+1][j+1]=0)\\ \min\{a[i+1][j+2],a[i+1][j]\}+1 &(a[i+1][j+1]\ne0)\\ \end{cases} $$

以此类推，$a[i][j](2\mid j)$ 表示从点 $(i,j)$ 开始，最多可以向上延伸出一个没有任何小三角形被蛀虫咬坏，边长为 $a[i][j]$ 的正三角形。我们可以得到：

$$a[i][j]=\begin{cases} 0 &(a[i][j]\text{的原值为}0)\\ 1 &(a[i-1][j-1]=0)\\ \min\{a[i-1][j-2],a[i-1][j]\}+1 &(a[i-1][j-1]\ne0)\\ \end{cases} $$

由此，我们可以写出这一部分的代码：

for(int i=n-1;i;i--)
	for(int j=1;j<=i;j++)
		if(a[i][(j<<1)-1]&&a[i+1][(j<<1)-1]
				&&a[i+1][j<<1]&&a[i+1][(j<<1)+1]){
			a[i][(j<<1)-1]=min(a[i+1][(j<<1)-1],
					a[i+1][(j<<1)+1])+1;
		}
for(int i=2;i<=n;i++)
	for(int j=2;j<i-1;j++)
		if(a[i][j<<1]&&a[i-1][(j<<1)-2]
				&&a[i-1][(j<<1)-1]&&a[i-1][j<<1]){
			a[i][j<<1]=min(a[i-1][(j<<1)-2],
					a[i-1][j<<1])+1;
		}

下一步，我们枚举一条分割线 $i$，将围巾分成两个部分：一个为顶点在最上方且边长为 $i$ 的正三角形，一个为剩余部分，使最终割下来的两个三角形一个在第一部分，一个在第二部分。然后就可以去枚举两个值 $x,y$，$x$ 为第一个三角形的最大面积；$y$ 为第二个三角形的最大面积。

我们就能通过枚举，得到每个分割线上下三角形面积和的最大值，代码如下：

int x=0,y=0;
for(int i=1;i<=n;i++){
	x=y=0;
	for(int j=1;j<=i;j++){
		for(int k=1;k<=j;k++)
			x=max(x,min(i-j+1,a[j][(k<<1)-1]));
		for(int k=1;k<j;k++)
			x=max(x,a[j][k<<1]);
	}
	for(int j=i+1;j<=n;j++){
		for(int k=1;k<=j;k++)
			y=max(y,a[j][(k<<1)-1]);
		for(int k=1;k<j;k++)
			y=max(y,min(j-i,a[j][k<<1]));
	}
	if(x&&y)ans=max(ans,x*x+y*y); //注意，x和y必须不为0
}

但是，这题我们还没做完，因为我们还没有考虑到下面这个情况：

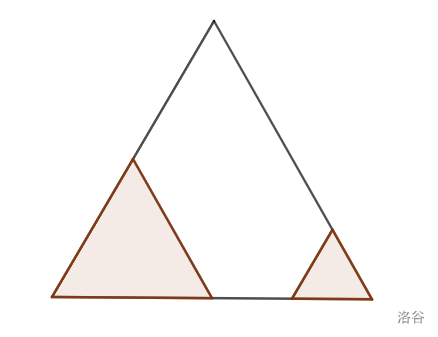
注：棕色为最大选取部分。

所以，我们应该把这个围巾旋转 $120°$，再继续 $dp$，当我们把三种情况都考虑完时，这个题目就做完了。

旋转部分代码：

void rotate(){
	for(int i=1;i<=n;i++){
		for(int j=1;j<=i;j++)
			temp[n-i+j][((n-i)<<1)+1]=a[i][(j<<1)-1]?1:0; //旋转尖端朝上的小三角形
		for(int j=1;j<i;j++)
			temp[n-i+j+1][(n-i+1)<<1]=a[i][j<<1]?1:0; //旋转尖端朝下的小三角形
	}
	for(int i=1;i<=n;i++)
		for(int j=1;j<=(i<<1)-1;j++)
			a[i][j]=temp[i][j]; //将旋转后的围巾拷贝到a里
}

完整代码：

#include<iostream>
using namespace std;
int n,m,ans=0;
int a[110][210]={0},temp[110][210]={0};
void calculate(){
	for(int i=n-1;i;i--)
		for(int j=1;j<=i;j++)
			if(a[i][(j<<1)-1]&&a[i+1][(j<<1)-1]
					&&a[i+1][j<<1]&&a[i+1][(j<<1)+1]){
				a[i][(j<<1)-1]=min(a[i+1][(j<<1)-1],
						a[i+1][(j<<1)+1])+1;
			}
	for(int i=2;i<=n;i++)
		for(int j=2;j<i-1;j++)
			if(a[i][j<<1]&&a[i-1][(j<<1)-2]
					&&a[i-1][(j<<1)-1]&&a[i-1][j<<1]){
				a[i][j<<1]=min(a[i-1][(j<<1)-2],
						a[i-1][j<<1])+1;
			}
	int x=0,y=0;
	for(int i=1;i<=n;i++){
		x=y=0;
		for(int j=1;j<=i;j++){
			for(int k=1;k<=j;k++)
				x=max(x,min(i-j+1,a[j][(k<<1)-1]));
			for(int k=1;k<j;k++)
				x=max(x,a[j][k<<1]);
		}
		for(int j=i+1;j<=n;j++){
			for(int k=1;k<=j;k++)
				y=max(y,a[j][(k<<1)-1]);
			for(int k=1;k<j;k++)
				y=max(y,min(j-i,a[j][k<<1]));
		}
		if(x&&y)ans=max(ans,x*x+y*y);
	}
}
void rotate(){
	for(int i=1;i<=n;i++){
		for(int j=1;j<=i;j++)
			temp[n-i+j][((n-i)<<1)+1]=a[i][(j<<1)-1]?1:0;
		for(int j=1;j<i;j++)
			temp[n-i+j+1][(n-i+1)<<1]=a[i][j<<1]?1:0;
	}
	for(int i=1;i<=n;i++)
		for(int j=1;j<=(i<<1)-1;j++)
			a[i][j]=temp[i][j];
}
int main(){
	ios::sync_with_stdio(false);
	cin>>n>>m;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=(i<<1)-1;j++)
			a[i][j]=1;
	for(int i=0,x,y;i<m;i++){
		cin>>x>>y;
		a[x][y]=0;
	}
	for(int i=0;i<3;i++){
		calculate();
		if(i!=2)rotate();
	}
	cout<<ans;
}

注： a<<1 是在 a 为整数时，a*2 的等价形式。