1 条题解
-
0
自动搬运
来自洛谷,原作者为

Godのfather
SMILE BACK搬运于
2025-08-24 21:24:40,当前版本为作者最后更新于2018-12-31 22:31:46,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
酒店之王解题报告
(一)前置技能
1.网络流最大流(, 都可以)
2.建图(邻接链表,反向边^1的小技巧)
达成了 1 阅读本文将很轻松,达成了 2 阅读代码将很轻松
(二)题目描述
简单地阐述一下题意:
有 个 类节点, 个 类节点, 个 类节点。每个 与一个 和一个 构成一组匹配(每个只能与给定的、匹配,且每个、只能匹配一个),求最大匹配数。
(三)解题思路
简化之后的题意很像二分图匹配,二分图匹配是一个点匹配一个点,而本题是一个点匹配两个点。
起先,我是想将 类节点放在左边, 类节点放中, 类最右。顺着题意用匹配和的,然后发现,这样子根本无法建图!!!
因为题目只给出了——, ——的关系,根本不知道与的关系。倘若按上面方式建图的话,和就会成为并列的节点。很明显这是不符合题意的。
那该如何建图呢?
既然已经知道与的关系、与的关系,不妨直接将放在中间,:
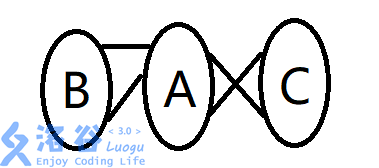
如此,得到了一张
三分图,再求此图的最大匹配即可。方法一:匈牙利算法
从出发直接向和跑两次二分图匹配即可。这里不作详细解释。
方法二:网络流最大流
按照网络流的正常操作,建立一个超级源点,连接所有,流量为1; 建立一个超级汇点, 使所有都连向,流量为1。再根据题目所给的关系连接——、——。
可能很多同学看到这里都会想:会了会了,然后再跑网络流最大流嘛。
不要以为这样就可以了。这可是
三分图匹配呀,哪有那么简单!看下面这幅图你就会知道哪里错了。
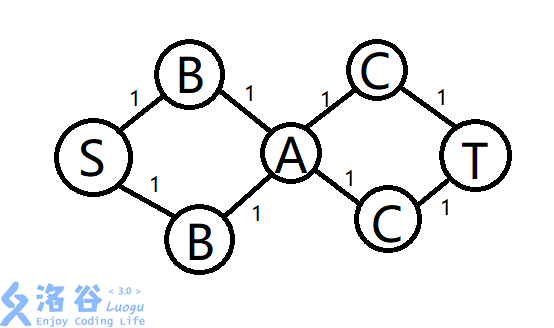
如果光是按上述方法建图的话,那么图就会变成上面那样,最大流跑出来是2。
然而我们知道,最大流不能是2,因为任意、只能匹配一个。
如何解决上述问题呢?
很简单,只需要将拆分为两个点即可,。
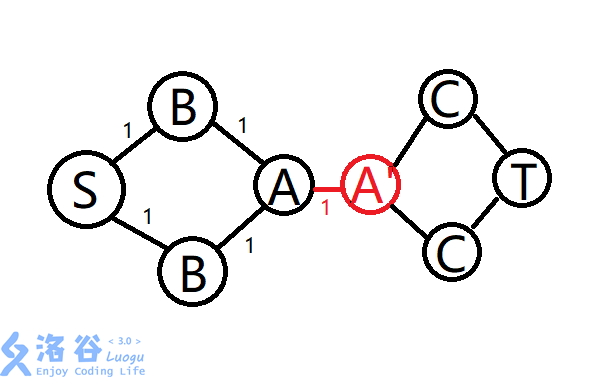
连接和,流量为1。
即可避免多个、重复匹配一个的情况了。
终于可以上代码了:(我太菜了,不会,所以只能写了)
#include<bits/stdc++.h> using namespace std; const int maxn = 105, maxm = 10000005, INF = 2147483647; int head[maxn<<2], ver[maxm], edge[maxm], Next[maxm], tot; void add(int x,int y,int z) { ver[++tot] = y, edge[tot] = z, Next[tot] = head[x], head[x] = tot; ver[++tot] = x, edge[tot] = 0, Next[tot] = head[y], head[y] = tot; } int n, p, q; //A:1~n, B:n+1~n+p, C:n+p+1~n+p+q, A':n+p+q+1~n+p+q+n int s, t, maxflow, incf[maxn<<2], pre[maxn<<2];bool vis[maxn<<2]; bool bfs() { for(int i=1; i<=n+p+q+n+2; i++) vis[i] = false; queue<int> Q; Q.push(s), vis[s] = true, incf[s] = INF; while(!Q.empty()) { int x = Q.front(); Q.pop(); for(int i=head[x]; i; i=Next[i]) if(edge[i]) { int y = ver[i]; if(vis[y]) continue; incf[y] = min(incf[x], edge[i]), pre[y] = i; vis[y] = true; if(y == t) return true; Q.push(y); } } return false; } void update() { int x = t; while(x!=s) { int i = pre[x]; edge[i] -= incf[t]; edge[i^1] += incf[t]; x = ver[i^1]; } maxflow+=incf[t]; } int main() { tot = 1; scanf("%d%d%d",&n,&p,&q); s = n+p+q+n+1, t = n+p+q+n+2; for(int i=1; i<=n; i++) for(int j=1; j<=p; j++) { bool x; scanf("%d",&x); if(x) add(j+n, i, 1); } for(int i=1; i<=n; i++) for(int j=1; j<=q; j++) { bool x; scanf("%d",&x); if(x) add(i+n+p+q, j+n+p, 1); } for(int i=1; i<=p; i++) add(s, i+n, 1); for(int i=1; i<=q; i++) add(i+n+p, t, 1); for(int i=1; i<=n; i++) add(i, i+n+p+q, 1); while(bfs()) update(); printf("%d", maxflow); return 0; }(四)总结
这道题是一道非常好的题目,它的建图方式很新颖。
网络流的题目考的无非就是建图,只要把图建好了,
还有什么题搞不掂?最后的最后,今天是2018的最后一天,祝大家在新的一年里RP++!更上一层楼!
- 1
信息
- ID
- 396
- 时间
- 1000ms
- 内存
- 125MiB
- 难度
- 6
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
