自动搬运

查看原文

来自洛谷，原作者为

	Jameswood 吾辈踯躅不前，无畏前路坎坷，无问同行无人，但忧道中花未央

搬运于2025-08-24 21:24:35，当前版本为作者最后更新于2019-02-04 19:46:30，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

说在前面的一些话

大致看了一眼题解，貌似各位大佬都是用 并查集 或者 dfs/bfs 或 图论 做的……其实并没有这个必要，而且唯一一个没有使用复杂算法的题解讲得也不是很清楚，也就斗胆写一篇了（那一篇写得质量实在是……）。

题目大意

已知有 $n$ 个点， $m$ 条边，每个点有一个权值 $h_i$ 。从一个点能够到达另一个点的条件是出发点的 $h_i$ 要大于**（注意没有等于）**抵达点的 $h_i$ （当然首先得有路才行）。

值得注意的一点是 $n,m$ 的范围极小，最大值只有 $300$ 。

大致思路以及所依论据（太烦不看或大佬版）：

首先记录所有可以通水的路径（即把因为高度因素不能通水的路径删去）。

然后将所有可以抵达的点标记出来，并记录总的数量（第一步以后所有边均为单向边），如果总数恰好为 n-1 且无法抵达的那个点恰好为高度最高点，那么 Okay ,不然就不行。

所以只要记录合法的通道数量和最高点的编号即可。

详细解法

我使用了一个非常暴力的做法，首先读入所有的高度，然后将所有可以通路的点与点之间的路径标记出来（因为数据范围极小所以我直接使用了邻接矩阵），这一步是在读入通道之前，读入高度之后进行的。

这一步的主要目的是为了之后 去除数据中有重复输入相同边的情况，其实 $vis$ 数组是不需要的，不过这样后面判断会很麻烦，末尾的 $AC$ 代码会给出写法，这里就不用了，以提高可读性。

同时下面这段代码也经过了一定的优化，如果无法理解，它的作用和这段代码是一致的（点击查看）。

//此处的 h[] 数组表示高度，vis 是用于表示是否合法的 bool 数组
for(int i=1;i<=n;i++){
	for(int j=i;j<=n;j++){
    	//只有两点高度相等的时候才没有路径
		if(h[i]==h[j]) continue;
		if(h[i]>h[j]){
			vis[i][j]=true;
		}else{
			vis[j][i]=true;
		}
	}
}

接下来读入所有的连通路径，并判断、记录这些路径中可以通水的数量以及可以抵达的点的编号（这就是前面的标记发挥作用的地方）。去除重复的路径的方法是每次把计完数的标记清除（设为无法通过）。

p.s. 先别问这些东东西西南南北北的有什么用，后面就知道了。

//vis[] 就是高度是否允许通行的标记，m 是输入路径的数量，counts 是符合要求的的路径的数量，get 就是抵达标记
for(int i=0;i<m;i++){
	scanf("%d%d",&x,&y);
	if(vis[x][y]==true){
		vis[x][y]=false;
        get[y]=true;
		++counts;
	}
	if(vis[y][x]==true){
		vis[y][x]=false;
        get[x]=true;
		++counts;
	}
}

后面就是核心的思想了！假设经过第一步的删除后有一份如下图所示的输入数据：

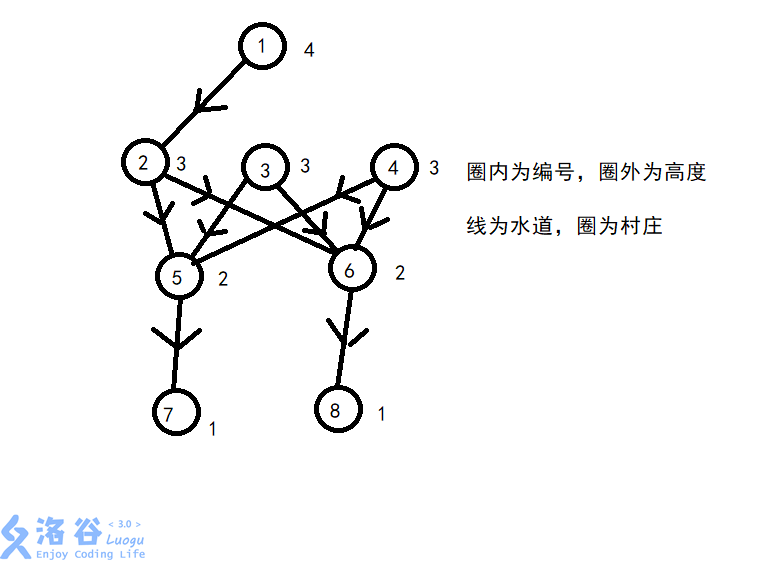
明显每一条边都是单向边，且这张图的回答应该是 “$Non$” （不行）。

仔细想一想，为什么呢？

关键点在于编号为 $3$ 、$4$ 的两个村庄，它们是无法被高度更高的村庄抵达的。所以可行的条件就很简单了：只需保证无法到达的点的个数为1，且这个点恰好为最高点就可以了。

重要的事情再说一边：

做法就比较简单了，首先记录一个不能抵达的点，接下来进行判断，如果不能抵达的点的数量小于总数-1亦或是不能抵达的点不是最高点（这个在输入的时候记录），那么就输出 $Non$ （判断为不行），否则就输出高度最高的村庄的编号。

p.s. 有些人可能会问，如果高度最高的村庄有两个肿么办？ 不要担心，这种情况肯定不行，因为至少有两个点是无法被到达的。

//counts 是符合条件的路径数量，n 是村庄总数，id 是高度最高的村庄的编号。
for(int i=1;i<=n;i++)
	if(get[i]==false){
		maxn=i;break;
	}
if(counts<n-1||maxn!=id){
	printf("Non\n");
}else{
	printf("Oui, j'ai trouve la solution.\n");
	printf("%d\n",id);
}

最后附上 $AC$ 代码：

#include<cstdio>
#include<cstdlib>
using namespace std;
const int SIZE=305;
int n,m,x,y,counts,h[SIZE],maxn=-1<<30,id;
bool get[SIZE];
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++){
		scanf("%d",&h[i]);
		if(h[i]>maxn){
			maxn=h[i];id=i;
		}
	}
	for(int i=0;i<m;i++){
		scanf("%d%d",&x,&y);
		if(h[x]>h[y]){
			if(get[y]!=true) ++counts;
			get[y]=true; 
		}
		if(h[y]>h[x]){
			if(get[x]!=true) ++counts;
			get[x]=true;
		}
	}
	for(int i=1;i<=n;i++)
		if(get[i]==false){
			maxn=i;break;
		}
	if(counts<n-1||maxn!=id){
		printf("Non\n");
	}else{
		printf("Oui, j'ai trouve la solution.\n");
		printf("%d\n",id);
	}
	return 0;
}

p.s. 个人感觉难度虚高，数据偏水，所以在最后的最后提供几组测试样例：

输入输出样例#2 , 输入输出样例#3 ， 输入输出样例#4