1 条题解
-
0
自动搬运
来自洛谷,原作者为

121017
???搬运于
2025-08-24 21:24:28,当前版本为作者最后更新于2020-10-24 02:04:59,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
不懂主席树的看这里~。
所谓主席树,乃可持久化线段树。至于为什么叫主席树,是因为发明人名字缩写是 。
因为主席树要记录历史版本,所以隔壁线段树的 就行不通了,于是码量就减少许多。
以至于很多时候我有种主席树比线段树水的错觉。
讲完主席树的定义,我们接下来再来了解主席树的实现,接下来我们看一棵普通线段树,它差不多长这样:
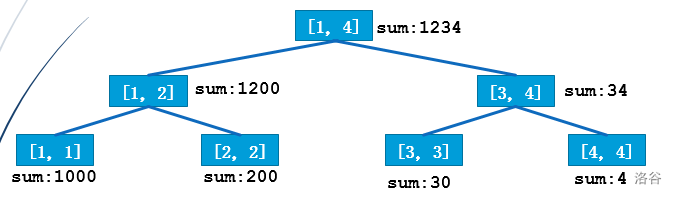
然后我们标记一下每次修改访问的节点:
修改第 个节点:
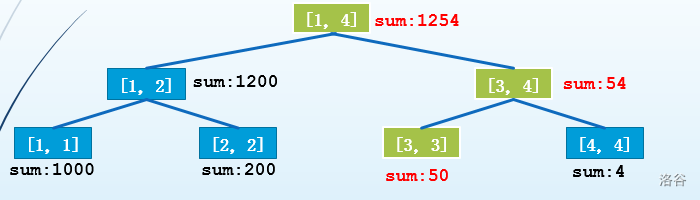
修改第 个节点:
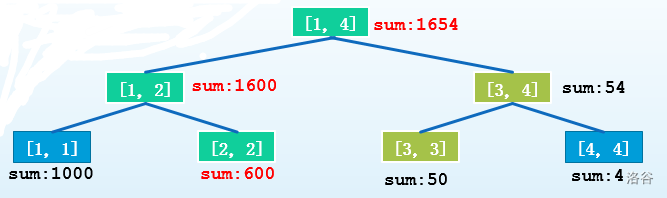
于是我们可以发现:每次修改只会修改 个节点,我们只要新增修改的节点就可以了。
主席树:
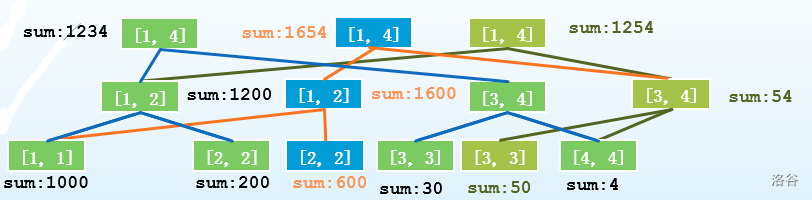
关于新增节点
我们不妨新增一个 数组表示当前子树节点个数,如果 ,则表示左子树满了,那么我们直接递归右子树;否则左子树还没满,就递归左子树。
code:
#include<bits/stdc++.h> #define ri register int #define int long long #define lc tree[p].l #define rc tree[p].r //懒人砖用表示法 using namespace std; int m,cnt=1,node; //cnt表示节点个数,node表示根节点个数 int root[10000001]; struct node{ int l; int r; char data; int size; }tree[10000001*4]; //如上 void change(int &p,int pre,int l,int r,char x){ p=++cnt; lc=tree[pre].l; rc=tree[pre].r; tree[p].size=tree[pre].size; tree[p].data=tree[pre].data; //先开点,继承上一个根节点 if(l>r) return; if(l==r){ tree[p].data=x; tree[p].size=1; return; } if(tree[lc].size==((l+r)>>1)-l+1) change(rc,tree[pre].r,(l+r)>>1+1,r,x); else change(lc,tree[pre].l,l,(l+r)>>1,x); //同上 tree[p].size=tree[lc].size+tree[rc].size;//当前子树的节点总数为左子树加上右子树 } char ask(int p,int l,int r,int x){ if(l>=r){ return tree[p].data; } if(x<=tree[lc].size){//如果要访问的叶子节点编号小于左子树的节点总数,那么ta肯定在左子树,反之在右子树 return ask(lc,l,(l+r)>>1,x); }else{ return ask(rc,(l+r)>>1+1,r,x-tree[lc].size); } } signed main(){ cin>>m; for(ri i=1;i<=m;i++){ char o,c; int x; cin>>o; if(o=='T'){ cin>>c; ++node; change(root[node],root[node-1],1,m,c); } if(o=='U'){ cin>>x; ++node; root[node]=root[node-x-1]; //撤销直接新建根节点就行了 } if(o=='Q'){ cin>>x; cout<<ask(root[node],1,m,x)<<endl; } } return 0; }点个赞再走呗~~~。
- 1
信息
- ID
- 380
- 时间
- 1000ms
- 内存
- 256MiB
- 难度
- 5
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
