自动搬运

查看原文

来自洛谷，原作者为

	Kenma 入得此门不回首，无需宣之于口

搬运于2025-08-24 21:24:24，当前版本为作者最后更新于2024-09-23 22:18:27，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

P1377 解题报告

前言

刚学笛卡尔树，遇到神仙题，写一篇题解加深印象。

如果我对笛卡尔树的认识有偏差，请指出并尽量不要开喷。

思路分析

首先简化题意：给定一棵依次插入元素的 BST，最小化 BST 插入元素序列的字典序（下称生成序列）。

考虑在 BST 的每个节点记录插入的权值 $k$，插入的时间戳 $t$，构成二元组 $(k,t)$。这样的一棵 BST 在权值维度满足 BST 的性质，在时间戳维度满足小根堆的性质。所以，题目给出的 BST 是一棵 Treap。

解释一下为什么在时间戳维度满足堆的性质。不难发现，后插入的节点的父亲一定是先插入的节点。其实，所有朴素构建的 BST 都是 Treap。

现在的问题变为，通过重新分配这棵 Treap 的节点的二元组中的 $t$ 的值，使其依然满足堆的性质的同时，最小化生成序列的字典序。

直接说可能有点抽象，我们以样例为例：

给定我们的生成序列为：$1,3,4,2$。

变为二元组：$(1,1),(3,2),(4,3),(2,4)$。

变成 BST：

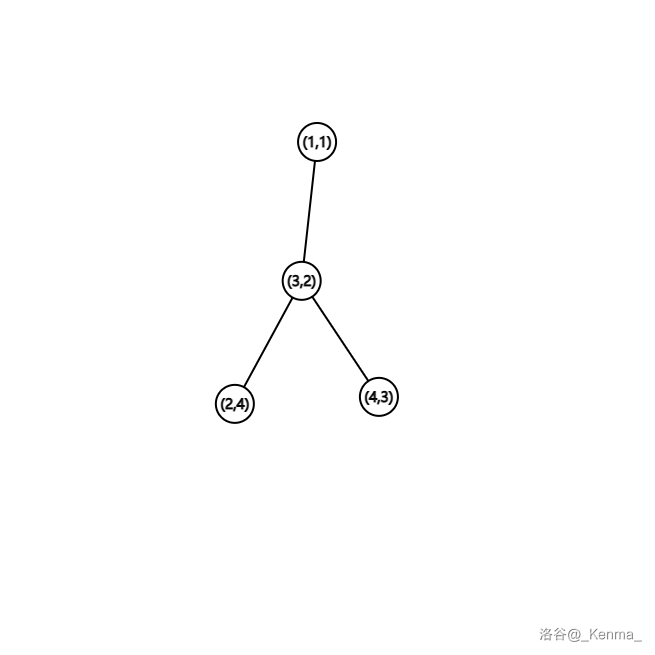
这样肯定不是最优的，不难发现，我们如果交换 $(3,2)$ 左右儿子的 $t$ 的值，可以使生成序列的字典序变得更小。

像这样：

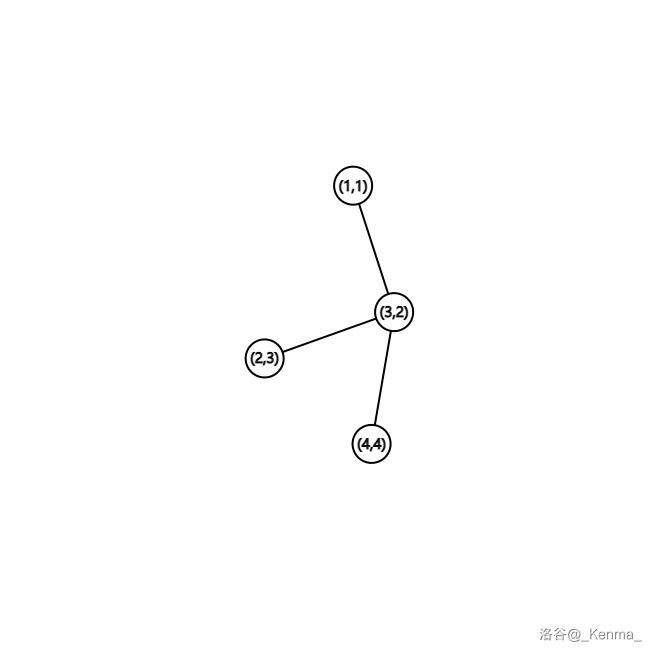
此时的生成序列：$1,3,2,4$。

考虑怎样分配时间戳 $t$ 是最优的。

注意到，因为要满足小根堆的性质，所以父亲的 $t$ 的值要大于其后代的 $t$ 的值。

又因为 Treap 满足 BST 的性质，贪心地考虑，将较小的 $t$ 分配给左子树，结果一定优于分配给右子树。

我们总结一下分配顺序：父亲 $>$ 左子树 $>$ 右子树。

注意到这就是对 BST 的前序遍历。

问题在于，按题意模拟构建 BST 的复杂度是 $O(n^2)$ 的，（但是能通过原题数据？），所以我们考虑更为高效的建树方法。

我们联想到，笛卡尔树的建树复杂度是 $O(n)$ 的，并且笛卡尔树也是 Treap，我们考虑怎样将本题中的 BST 转化为笛卡尔树。

考虑笛卡尔树和本题 BST 的区别仅在于二元组的先后顺序不同。具体地，笛卡尔树是权值维度 $k$ 满足堆的性质，时间戳维度 $t$ 满足 BST 的性质。而本题的 BST 恰好相反。所以，我们只需要交换二元组的顺序，就可以仿照笛卡尔树 $O(n)$ 建树了。

具体实现很简洁（至少比我讲的简洁）。考虑正常笛卡尔树的生成序列 $a$，本质上是二元组 $(a_i,i)$，而本题中二元组为 $(i,a_i)$。把序列 $a$ 的下标和值交换就行了。

代码实现

代码实现很简洁，只要理解了笛卡尔树和 Treap 的关系，就很容易写出代码。

#include<bits/stdc++.h>
using namespace std;
int n,x,a[100005],ls[100005],rs[100005],vis[100005],flag;
void dfs(int x){
	cout<<x<<' ';
	if(ls[x]) dfs(ls[x]);
	if(rs[x]) dfs(rs[x]);
}
stack<int> s;
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0); 
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>x;
		a[x]=i;
	}
	for(int i=1;i<=n;i++){
		flag=0;
		while(s.size() && a[s.top()]>a[i]) flag=s.top(),s.pop();
		if(s.size()) rs[s.top()]=i;
		if(flag) ls[i]=flag;
		s.push(i);
	} 
	for(int i=1;i<=n;i++){
		vis[ls[i]]=1;
		vis[rs[i]]=1;
	}
	for(int i=1;i<=n;i++){
		if(!vis[i]){
			dfs(i);
			break;
		}
	}
	return 0;
}

注意到没有任何细节。

后记

这是一道考察选手对 Treap 和笛卡尔树理解的思维好题，构造精妙和谐，让人耳目一新。