自动搬运

查看原文

来自洛谷，原作者为

	jun头吉吉 alive

搬运于2025-08-24 21:24:12，当前版本为作者最后更新于2020-07-09 13:19:41，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题意

给定一些物品，可以放在$A$或$B$中，取得不同收益。 某些物品同时放在$A$或$B$中，可以获得额外收益。 求收益的最大值。

题解

看到二者选其一，我们不禁联想到了最小割模型

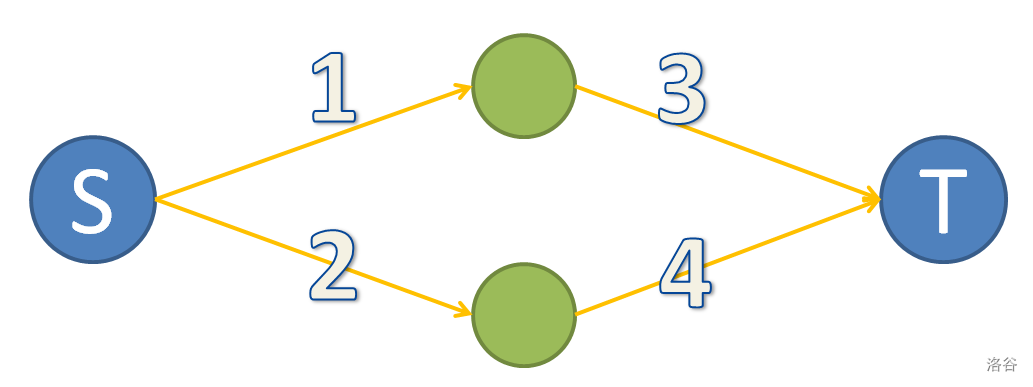
很明显，这道题主要的问题在于建模。若是不考虑额外收益，图是很容易建出来的 ：

• 由源点$S$向它连一条边权为其种在$A$中的价值的边，表示将其种在$A$中；
• 由它向汇点$T$连一条边权为其种在$B$中的价值的边，表示将其种在$B$中；
• 把一条边割掉，则表示不这么种。

这样的图，要使其不连通，每个点都不能同时连接源点$S$和汇点$T$，也就是说，保证其只属于一个集合

这时跑一遍最小割，是删去的最小，留下的就是最大的了 假装不能直接取最大值

但是现在加入了额外收益，应该如何改进上述的图呢？

通过对题意的了解，我们知道：

1. 如果割掉了$1$、$2$，那么把边权为$c_{1}$的边也要割掉
2. 如果割掉了$3$、$4$，那么把边权为$c_{2}$的边也要割掉
3. 如果割掉了$1$、$4$或者$2$、$3$，那么两条边都要割掉

此时，我们已经大致想到此图的构图方法了。由$1$、$2$我们了解到，$c_1\ \ c_2$应该分别与$1\text{、}2$，$3\text{、}4$并联 电学乱入，于是我们瞎搞思考出了下图：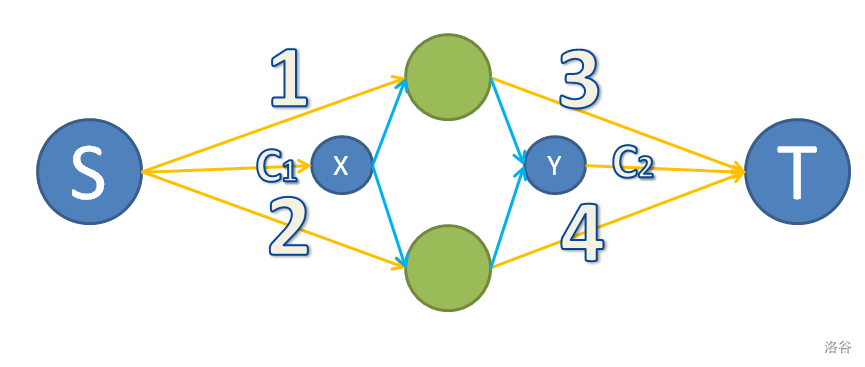

其中$\color{SkyBlue}{\text{蓝色}}$ 的边边权是$+\infty$，是不能删除的

我们发现，此图非常符合题目的限制。于是我们建个图套个板子就A了

#pragma GCC optimize(3,"Ofast","inline")
#include<bits/stdc++.h>
namespace in{
	char buf[1<<21],*p1=buf,*p2=buf;
	inline int getc(){
	    return p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++;
	}
	template <typename T>inline void read(T& t){
	    t=0;int f=0;char ch=getc();
	    while (!isdigit(ch)){
	        if(ch=='-')f = 1;
	        ch=getc();
	    }
	    while(isdigit(ch)){
   	    	t=t*10+ch-48;
   	    	ch = getc();
   		}
		if(f)t=-t;
	}
	template <typename T,typename... Args> inline void read(T& t, Args&... args){
	    read(t);read(args...);
	}
}
namespace out{
	char buffer[1<<21];
	int p1=-1;
	const int p2 = (1<<21)-1;
	inline void flush() {
		fwrite(buffer,1,p1+1,stdout),
		p1=-1;
	}
	inline void putc(const char &x) {
		if(p1==p2)flush();
		buffer[++p1]=x;
	}
	template <typename T>void write(T x) {
		static char buf[15];
		static int len=-1;
		if(x>=0){
			do{
    			buf[++len]=x%10+48,x/=10;
    		}while (x);
		}else{
    		putc('-');
			do {
    			buf[++len]=-(x%10)+48,x/=10;
			}while(x);
		}
		while (len>=0)
			putc(buf[len]),--len;
	}
}
using namespace std;
const int maxn=40010,maxe=1000010*2;
struct Graph{
	struct node{
		int v,w,nxt;
	}e[maxe<<1];
	int head[maxn],cur[maxn],tot;
	int dis[maxn];
	int s,t;
	void init(int _s,int _t){s=_s,t=_t;tot=1;memset(head,0,sizeof head);}
	Graph(int _s=0,int _t=0){init(_s,_t);}
	void add(int u,int v,int w){
		//printf("%d %d %d\n",u,v,w);
		e[++tot]=(node){v,w,head[u]},head[u]=tot;
		e[++tot]=(node){u,0,head[v]},head[v]=tot;
	}
	#define v e[i].v
	inline bool bfs(){
		queue<int>q;
		memset(dis,0,sizeof dis);
		memcpy(cur,head,sizeof head);
		dis[s]=1;q.push(s);
		while(q.size()){
			int u=q.front();q.pop();
			for(int i=head[u];i;i=e[i].nxt)
				if(!dis[v]&&e[i].w){
					dis[v]=dis[u]+1,q.push(v);
					if(v==t)return true;
				}
		}
		return  false;
	}
	int dfs(int u,int flow){
		if(u==t)return flow;
		int rest=flow;
		for(int i=cur[u];i&&rest;i=e[i].nxt){
			if(dis[v]==dis[u]+1&&e[i].w){
				int tmp=dfs(v,min(rest,e[i].w));
				rest-=tmp,e[i].w-=tmp,e[i^1].w+=tmp;
			}
			cur[u]=i;
		}
		if(rest==0)dis[u]=-1;
		return flow-rest;
	}
	#undef v
	int dinic(){
		int ans=0;
		while(bfs())
			while(int sth=dfs(s,2e9))
				ans+=sth;
		return ans;
	}
}G;
int n,m,c[1000],tot;
int sum=0;
signed main(){
	//freopen("1.in","r",stdin);
	G.init(1000+1000*4+100,1000+1000*4+101); 
	in::read(n);tot=n;
	for(int i=1;i<=n;i++){
		int tmp;in::read(tmp);
		G.add(G.s,i,tmp);
		sum+=tmp;
	}
	for(int i=1;i<=n;i++){
		int tmp;in::read(tmp);
		G.add(i,G.t,tmp);
		sum+=tmp;
	}
	in::read(m);
	for(int i=1;i<=m;i++){
		int k,c1,c2,tmp;
		in::read(k,c1,c2);
		G.add(G.s,tot+1,c1);
		G.add(tot+2,G.t,c2);
		sum+=c1+c2;
		for(int j=1;j<=k;j++){
			in::read(tmp);
			G.add(tot+1,tmp,2e9);
			G.add(tmp,tot+2,2e9);
		}
		tot+=2;
	}
	out::write(sum-G.dinic());
	out::flush();
	return 0;
}