自动搬运

查看原文

来自洛谷，原作者为

	AuCloud 这只小羊很懒，什么都没留下来

搬运于2025-08-24 21:24:07，当前版本为作者最后更新于2019-01-08 21:01:59，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

题面

我太弱了

来讲讲我是怎么想的

题意很好理解，不多啰嗦

---

顶点

顶点肥肠简单~~(对于我来说)~~

直接判断是否重合(x1=x2且y1=y2)

if(xx==x1&&yy==y1 || xx==x2&&yy==y2 || xx==x3&&yy==y3)
{
	cout<<'4';
	return 0; 
}

---

边

(划重点)

首先看看图↓

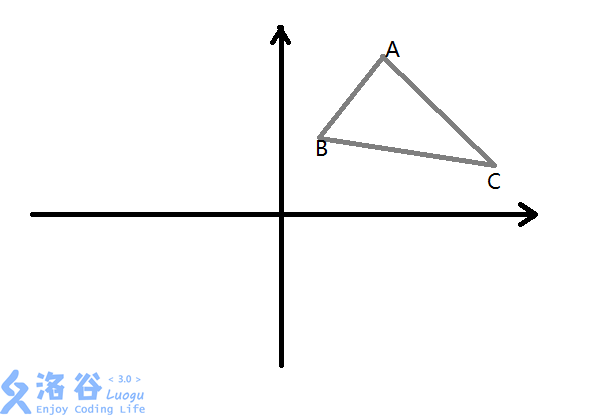
我们可以把AB，AC，BC延长成直线

如图↓

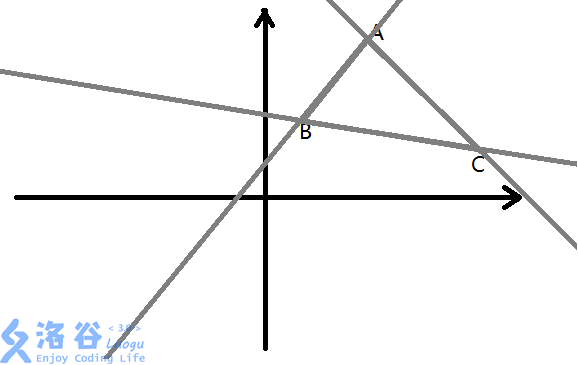
然后……

求AB、AC、BC的一次函数解析式，并判断是否在直线上且在两点之间

至于公式嘛。。。

自己推去

k1=(y1-y2)/(x1-x2)

b1=y1-k1·x1

但是注意！

如果x1=x2的话(就是一条垂直于X轴的直线)

会RE。。。

所以要特判的

double k1,b1;
if(x1==x2)//特判 
{
	k1=b1=-888888;//(洛谷保佑我AC叭)
	if(x1==xx&&(yy>y2&&yy<y1||yy<y2&&yy>y1))
	{
		cout<<'3';
		return 0;
	} 
}
else 
{
	k1=(y1-y2)/(x1-x2);
	b1=y1-k1*x1;
}
	

酱紫

---

三角形外(内)

(仍然是个重点)

(这个点卡了好久)

继续画图↓

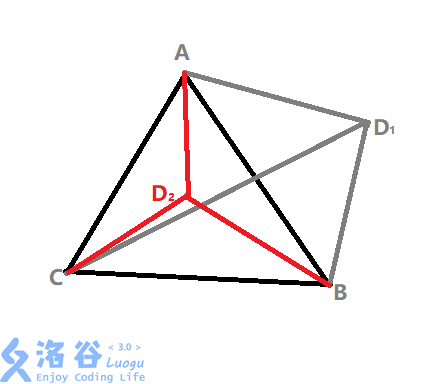
D1 在外，D2 在内

观察力好一点的盆友们应该能看出来

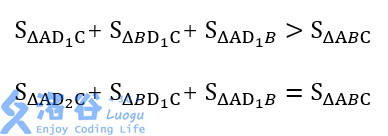
我们可以利用这个性质，判断D在内在外啦~~~

然而！问题来了

怎么算面积呢？？？

当然是我们的海伦公式啦

像酱紫

double si(int a,int b,int c,int d,int e,int f)
{
	double hehe,ab,ac,bc;
	ab=sqrt((a-c)*(a-c)+(b-d)*(b-d));//勾股定理求两点之间距离 
	ac=sqrt((a-e)*(a-e)+(b-f)*(b-f));//同上 
	bc=sqrt((x-e)*(x-e)+(d-f)*(d-f));//同上 
	hehe=(ab+ac+bc)/2;
	return sqrt(hehe*(hehe-ab)*(hehe-ac)*(hehe-bc));//海伦公式 
}

(链：例题)

double S_abc,S_acd,S_abd,S_bcd;//四个三角形，一大三小 
S_abc=si(x1,y1,x2,y2,x3,y3);
S_acd=si(x1,y1,x3,y3,xx,yy);
S_abd=si(x1,y1,x2,y2,xx,yy);
S_bcd=si(x2,y2,x3,y3,xx,yy);

求出面积后，就可以愉快地AC啦

---

最后，奉上代码

#include<iostream>
#include<cmath>
using namespace std;
double si(int a,int b,int x,int y,int n,int m)
{
	double hehe,ab,ac,bc;
	ab=sqrt((a-x)*(a-x)+(b-y)*(b-y));//勾股定理求两点之间距离 
	ac=sqrt((a-n)*(a-n)+(b-m)*(b-m));//同上 
	bc=sqrt((x-n)*(x-n)+(y-m)*(y-m));//同上 
	hehe=(ab+ac+bc)/2;
	return sqrt(hehe*(hehe-ab)*(hehe-ac)*(hehe-bc));//海伦公式 
}
int main()
{
	int x1,x2,x3,y1,y2,y3,xx,yy;
	char ch;//格式控制用 
	cin>>ch>>x1>>ch>>y1>>ch;//第一个点 
	cin>>ch>>x2>>ch>>y2>>ch;//第二个点 
	cin>>ch>>x3>>ch>>y3>>ch;//第三个点 
	cin>>ch>>xx>>ch>>yy>>ch;//问题点 
	
	if(xx==x1&&yy==y1 || xx==x2&&yy==y2 || xx==x3&&yy==y3)//直接判断顶点 
	{
		cout<<'4';
		return 0; 
	}
	
	double k1,b1;//1-2
	if(x1==x2)//防止除以零 
	{
		k1=b1=-888888;
		if(x1==xx&&(yy>y2&&yy<y1||yy<y2&&yy>y1))
		{
			cout<<'3';
			return 0;
		} 
	}
	else 
	{
		k1=(y1-y2)/(x1-x2);
		b1=y1-k1*x1;
	}
	double k2,b2;//1-3
	if(x1==x3)
	{
		k2=b2=-888888;
		if(x1==xx&&(yy>y3&&yy<y1||yy<y3&&yy>y1))
		{
			cout<<'3';
			return 0;
		}
	}
	else
	{
		k2=(y1-y3)/(x1-x3);
		b2=y3-k2*x3;
	}
	double k3,b3;//2-3
	if(x3==x2)
	{
		k3=b3=-888888;
		if(x3==xx&&(yy>y2&&yy<y3||yy<y2&&yy>y3))
		{
			cout<<'3';
			return 0;
		}
	}
	else
	{
		k3=(y3-y2)/(x3-x2);
		b3=y2-k3*x2;
	}
	
	if(yy==xx*k1+b1&&(xx<x1&&xx>x2||xx>x1&&xx<x2) || yy==xx*k2+b2&&(xx<x1&&xx>x3||xx>x1&&xx<x3) || yy==xx*k3+b3&&(xx<x3&&xx>x2||xx>x3&&xx<x2))
	{
		cout<<'3';
		return 0;
	}
	
	double S_abc,S_acd,S_abd,S_bcd;//四个三角形，一大三小 
	S_abc=si(x1,y1,x2,y2,x3,y3);
	S_acd=si(x1,y1,x3,y3,xx,yy);
	S_abd=si(x1,y1,x2,y2,xx,yy);
	S_bcd=si(x2,y2,x3,y3,xx,yy);
	if(S_acd+S_abd+S_bcd>S_abc)
	{
		cout<<'2';
		return 0;
	}
	
	cout<<'1';
	return 0;
}

(这是第一次这么认真地写题解，望通过)