自动搬运

查看原文

来自洛谷，原作者为

	lei_yu 这个人很菜，什么也留不下

搬运于2025-08-24 21:23:32，当前版本为作者最后更新于2019-08-07 10:04:22，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

这是一道看起来很水的题目，这里我来讲一下具体解法给刚开始学的同胞们。

首先讲一讲思路

看一下下面这个乘法的过程

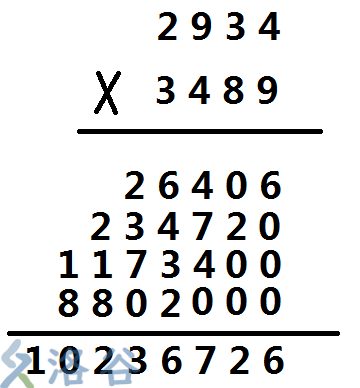
（非常的大，肯定不是人算的，所以我们需要电脑）

我们在计算的时候是计算2934乘下面的每一位最后加起来。（强颜欢笑）

然而需要注意的是，我们在这样计算的时候，最后是加法是错位的（如上图），因此我们在计算的时候需要注意这一点。

接下来是具体的计算过程：

首先将两个特别大的数字读入字符串，然后倒着放进一维数组 （和高精度加法一样）；

cin>>a1>>b1;
int lena=strlen(a1);
int lenb=strlen(b1);
for(i=1;i<=lena;i++)a[i]=a1[lena-i]-'0';
for(i=1;i<=lenb;i++)b[i]=b1[lenb-i]-'0';

接下来，不难想到，在计算乘法的时候可以使用两个循环进行枚举，以上面的图片为例子：外循环i为3489，内循环j为2934。 (你想想自己怎么算乘法的)

数组c作为答案数组，在枚举时令c[i+j-1]+=a[i] * b[j];

for(i=1;i<=lenb;i++)
for(j=1;j<=lena;j++)
c[i+j-1]+=a[j]*b[i];

在计算乘法的时候先不考虑进位，之后再加上去就行。但是为什么是i+j-1呢，事实上，j是指正常的计算进位（一位一位进行乘法计算），而i就是我们说的错位相加。

在进行枚举计算之后,我们的c数组就成为了没有进位的答案,如下图

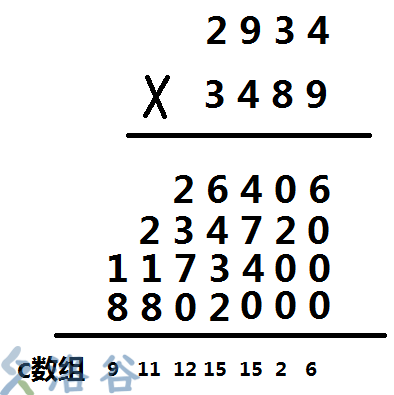
之后，我们只需要对c数组进行进位操作就好了。

for(i=1;i<lena+lenb;i++)//无论数字如何大，数位也不会大于两个乘数的和
if(c[i]>9)//大于9则需要进位
{
	c[i+1]+=c[i]/10;
	c[i]%=10;
}

最后,我们还需要一个去除数字首多余的0的操作，同加法。

len=lena+lenb;
while(c[len]==0&&len>1)len--;

最后的最后,我们只需要将数字输出就好了

for(i=len;i>=1;i--)cout<<c[i];
return 0;//华丽的结束

那么最后附上AC代码

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
char a1[10001],b1[10001];
int a[10001],b[10001],i,x,len,j,c[10001];
int main ()
{
    cin>>a1>>b1;//不解释，不懂看前面
    int lena=strlen(a1);//每个部分都很清楚
	int lenb=strlen(b1);//这只是方便你们复制
    for(i=1;i<=lena;i++)a[i]=a1[lena-i]-'0';
    for(i=1;i<=lenb;i++)b[i]=b1[lenb-i]-'0';
	for(i=1;i<=lenb;i++)
	for(j=1;j<=lena;j++)
	c[i+j-1]+=a[j]*b[i];
    for(i=1;i<lena+lenb;i++)
	if(c[i]>9)
	{
		c[i+1]+=c[i]/10;
		c[i]%=10;
	}
	len=lena+lenb;
    while(c[len]==0&&len>1)len--;
    for(i=len;i>=1;i--)cout<<c[i];
    return 0;
}