自动搬运

查看原文

来自洛谷，原作者为

	feizhu_QWQ 谈笑有鸿儒，往来无白丁

搬运于2025-08-24 21:23:11，当前版本为作者最后更新于2025-08-09 14:07:00，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

首先，在写这道题之前，我们要先了解排序是个什么东西。

举个例子：给你一个数组 $2,5,3,1$，让你把他从小到大排序，你一定会，排完就是 $1,2,3,5$。
可如何用程序实现呢？
我们会讲 $9$ 种方法。
我们从易到难：

1. 快速排序（系统）

在 C++ 的 stl 库里有这样一个函数：sort()。
我们简称快排，快速排序。
他的实现原理我们下一种方法会将，我们这里只需要知道它的实现方法：sort([数组名]+1,[数组名]+1+n);（省略中括号）。运行之后，数组就会变成从小到大的样子，你就会获得一个从小到大的数组了，他的时间复杂度是 $n \log n$。
实现：

#include<bits/stdc++.h>
using namespace std;
int a[20000005];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=m;i++)
    {
    	cin>>a[i];//输入
	}
	sort(a+1,a+1+m);//stl排序
	for(int i=1;i<=m;i++)
	{
		cout<<a[i]<<" ";
	}
	return 0;
}

2. 快速排序（手写）

上个方法我们介绍了排序的 stl，这里我们来介绍的是他的实现方式。
想一想，我们有一个东西，比他小的数放左边，大的放右边，就可以把他们分类了。
我们可以每次选择一个基准数，当然，我们一般用随机数，那么我们以这个基准数为准，比他小的放左边，比他大的放右边，就会得到一个较为有序的数组。
但很明显，这不是完全从小到大的，所以我们又用到分治的思想：

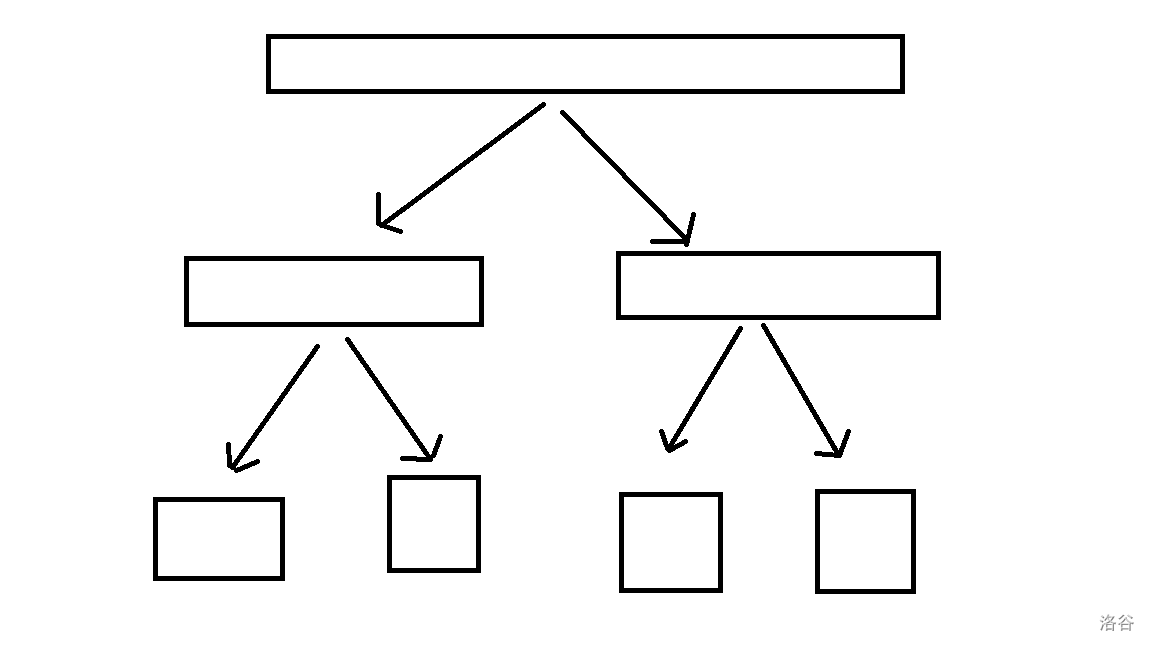
我们生活中有一句话“大事化小，小事化了” 在程序设计中，这也同样可行。
比如一个数组求最大值的问题，给你一个长度为 $4$ 的数组，让你求这个数组的最大值，我们可以换一种思路：
给你 1 5 2 6。
我们把 1 5 拿出来，再把 2 6 拿出来。
1 5 的最大值很明显我们用 $\max$ 函数得出来是 5，2 6 是 6。
我们再把两个最大值 5 6 比大小，得出来 6。
这就是分治的典型案例，整个数组无法直接比大小，我们就把他分成小数组求，然后把小数组得来的答案往上传，和另一个小数组比较，循环往复，就得到了最终答案。

因为单纯一次基准数比较无法得出答案，我们就把基准数左边的数组再找一个基准数来排序，右边同理。
我们可以用函数递归的方法实现，那么最后，数组就排好序了，这样我们有 $\log$ 次的排序，每次约等于 $n$，那么总的时间复杂度大概是 $n \log n$，同样优秀。
因为大家习惯用 stl，所以手写并不常用。
实现：

#include<bits/stdc++.h>
using namespace std;
int a[1000005];
int n,m;
void qiuck_sort(int l,int r)
{
	if(l>=r) return;
	int mid=rand()%(r-l+1)+l; //随机基准数
	int t=a[mid];
	int q=l,h=r;
	a[mid]=a[l];
	while(q<h)
	{
		while(q<h&&a[h]>=t)//大的放右边
		{
			h--;
		}
		a[q]=a[h];
		while(q<h&&a[q]<=t)//小的放左边
		{
			q++;
		}
		a[h]=a[q];
	}
	qiuck_sort(l,q-1);//继续递归
	qiuck_sort(q+1,r);
	return;
}
int main()
{
	srand(time(0));//用随机数一定要加这句话
	cin>>n>>m;
	for(int i=1;i<=m;i++) cin>>a[i];
	qiuck_sort(1,m);
	for(int i=1;i<=m;i++) cout<<a[i]<<" ";
	return 0;
}//此代码正确性无法保证，随机性强

3. 归并排序

快速排序用递归实现，我们也可以用递归分治的思想，创造另一种算法。
同样是排序，现在给你两个有序的数组，怎么把他们融合在一起，变成一个同样有序的数组？
这里可以用到指针，我们从左到右，如果当前第一个数组的第一个数，比第二个数组的第一个数小，就先把前者放入一个新数组里，然后把原数组里的这个数删除，这样，我们就能得到新数组了。
我们来模拟一下这个过程：
1 4 5 和 2 3 6。
首先，两个数组的第一个数分别是 $1$ 和 $2$，$1$ 更小，优先加入 $1$。
接着，两个数组的第一个数分别是 $4$ 和 $2$，$2$ 更小，优先加入 $2$。
接着，两个数组的第一个数分别是 $4$ 和 $3$，$3$ 更小，优先加入 $3$。
接着，两个数组的第一个数分别是 $4$ 和 $6$，$6$ 更小，优先加入 $6$。
接着，两个数组的第一个数分别是 $5$ 和 $6$，$5$ 更小，优先加入 $5$。
最后只剩下了 $6$，我们把 $6$，放在最后，就得到了 1 2 3 4 5 6 这样的一个有序数组。
那么我们怎么得到两个有序的数组呢？
这就是递归的事了。
我们每次递归先直接调用函数，等着他把两个有序的数组传上来，我们再履行自己的职责，把这两个有序数组合并。
归并排序很明显比其他排序复杂，所以他一般被用来求逆序对（我们到时候再说）。
实现：

#include<bits/stdc++.h>
using namespace std;
int a[1000005],b[1000005];
int n,m;
void merge_sort(int l,int r)
{
	int mid=(l+r)/2;
	int q=l,h=mid+1,cnt=0;//这里的数组是连在一起的有序数组，所以我们从中间断开
	while(q<=mid&&h<=r)
	{
		if(a[q]<=a[h])//如果第一个数小
		{
			cnt++;
			b[cnt]=a[q];
			q++;
		}
		else//第二个数小
		{
			cnt++;
			b[cnt]=a[h];
			h++;
		}
	}
	while(q<=mid)
	{
		cnt++;
		b[cnt]=a[q];
		q++;
	}
	while(h<=r)
	{
		cnt++;
		b[cnt]=a[h];
		h++;
	}
	for(int i=1,j=l;i<=cnt;i++,j++)
	{
		a[j]=b[i];
	}
	return;
}
void m_sort(int l,int r)
{
	if(l>=r) return;
	int mid=(l+r)/2;
	m_sort(l,mid);
	m_sort(mid+1,r);//先往下递归
	merge_sort(l,r);//再履行自己的职责
	return;
}
int main()
{
	cin>>n>>m;
	for(int i=1;i<=m;i++) cin>>a[i];
	m_sort(1,m);
	for(int i=1;i<=m;i++) cout<<a[i]<<" ";
	return 0;
}

4. 桶排序

桶排序的时间复杂度取决于这个数的大小，在有些地方有奇效。
我们想，C++ 中有什么东西是有序的？
数组下标！
数组下标一般都是从 $1$ 到 $n$ 的，明显有序，所以我们就可以用这个性质来排序。
因为数字是可能重复的，所以我们拿一个数组来记录每个数字出现的数量。
最后，我们从 $1$ 到极大值遍历这个记录数组，他出现了几次就输出几个他。
因为这个过程有点像往木桶里丢小球，所以我们简称桶排序。
实现：

#include<bits/stdc++.h>
using namespace std;
int tong[10000005];
int n,m;
int main()
{
   cin>>n>>m;
   for(int i=1;i<=m;i++)
   {
   	int x;
   	cin>>x;
   	tong[x]++;//记录数出现的次数

   }
   for(int i=1;i<=n;i++)
   {
   	for(int j=1;j<=tong[i];j++) cout<<i<<" ";//
出现几次输出几次
   }
   return 0;
}

5. 堆排序

堆排序纯粹依靠另一种数据结构 - 堆，学名优先队列，但和队列没有关系。
堆，他的操作有以下几种：
priority_queue<int> q 定义一个叫做 $q$，类型为 $int$ 的堆。（默认是大根堆，就是返回最大值，如果要最小值，我们这样写：priority_queue<int,vector<int>,greater<int> >
q.push(x); 往名为 $q$ 的堆里放入元素 $x$。
q.pop(); 删除堆 $q$ 中最大的元素。
q.top() 返回堆 $q$ 中最大的元素是多少。
（注意以上两个操作不能在堆为空的时候使用）。
q.size() 返回堆 $q$ 中的元素数量。

很明显，他可以把当前最大的元素告诉你，那我们就可以利用他排序。
一开始我们先把所有元素塞入这个堆，然后我们每次输出堆的最小值（所以我们要用上面的第二种定义），然后把最小值丢出去，再进行上面的操作，就可以排完序了。
因为堆单次操作的时间复杂度是 $\log$，我们有 $n$ 个元素，所以时间复杂度还是 $n \log n$。
实现：

#include<bits/stdc++.h>
using namespace std;
int n,m;
priority_queue<int,vector<int>,greater<int> > q;//定义小根堆
int main()
{
	cin>>n>>m;
	for(int i=1;i<=m;i++)
	{
		int x;
		cin>>x;
		q.push(x);//把元素塞入数组
	}
	while(q.size()>0)
	{
		cout<<q.top()<<" ";//输出最小值
		q.pop();//弹出最小值
	}
	return 0;
}

警惕，下面是三种时间复杂度很高的算法，且无法AC此题

6. 冒泡排序

上面我们都是从整体考虑问题，这里我们从个体来看待。
假如我们只用 x<y 这一个东西，能否完成一整个数组的排序呢？当然可以！
想想，我们是不是可以每次加入一个数，然后把他放入我们的新数组中？
但我们该如何把这个新进来的元素归位呢？一个一个比大小！
首先保证我们是上个数已经正确归位了才来处理这个元素的，所以我们的新数组一定是有序的！
我们先把他放在数组最后面，然后我们把它和他前面的一个元素比大小，如果我们的新元素更小，就把他和前面的元素换个位置，然后到了下一个位置，继续和下一个元素比，重复操作，直到出现了比新元素更小的元素，或者已经到了第一个元素，就停止，然后处理下一个新进来的元素。
这样，旧数组里的所有数解决完，我们就排完序啦！
因为这种相邻元素比大小很像冒泡泡（我不觉得）所以叫冒泡排序。
总的下来时间复杂度是 $n^2$，很不建议使用，但一定要知道。
实现：

#include<bits/stdc++.h>
using namespace std;
int a[1000005];
int n,m;
bool cmp(int q,int h)
{
	return q<h;
} 
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=m;i++)
	{
		cin>>a[i];
	}
	for(int i=1;i<=m;i++)
	{
		for(int j=1;j<i;j++)//往前移动
		{
			if(a[j]>a[i])//比大小
			{
				swap(a[i],a[j]);
			}
                        //这里可以选择跳出循环，但不跳出也不会出BUG，既然已经有比我小的了，前面的肯定更小
		}
	}
	for(int i=1;i<=m;i++) cout<<a[i]<<" ";
	return 0;
}

7. 选择排序

其实选择排序就是不用堆的堆排序。
听起来很神奇的样子。
堆排序是每次拿出最小值，是 $\log$ 的时间，但我们可以直接循环找最小值啊！不要忘本！
我们先在旧的数组中循环，找到一个最小的值，然后把他放到新数组里，接着再找最小值，循环往复，最后结束。
$n^2$ 不建议使用。 实现：

#include<bits/stdc++.h>
using namespace std;
int a[1000005];
int n,m;
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=m;i++)
	{
		cin>>a[i];
	}
	for(int i=1;i<=m;i++)
	{
		int minn=2e9,ans=0;//准备找最小值
		for(int j=i;j<=m;j++)
		{
			if(a[j]<minn)//比较
			{
				minn=a[j];//找到最小值
				ans=j;//更新答案位置
			}
		}
		swap(a[i],a[ans]);//放入新数组，这样也没问题
	}
	for(int i=1;i<=m;i++) cout<<a[i]<<" ";
	return 0;
}

8. 插入排序

插入是什么意思？在一个位置插入一个元素。
那我们也是从旧数组中拿出新元素，塞入新数组里。
怎么塞？我们找到合适的位置就行了。
其实插入就是冒泡的改版，我们找到第一个比他小的数，然后把新的元素插在他前面就好啦！
所以插的时候我们要把他后面的数往后挪一格，给他腾出位置。
$n^2$ 不建议用。
实现：

#include<bits/stdc++.h>
using namespace std;
int a[1000005],ans[1000005];
int n,m;
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=m;i++)
	{
		cin>>a[i];
	}
	for(int i=1;i<=m;i++)
	{
		int id=0;
		for(int j=1;j<=i;j++)
		{
			id=j;
			if(a[i]<ans[j])//找到第一个比他小的
			{
				break;
			}
		}
		for(int j=i;j>=id;j--)
		{
			ans[j+1]=ans[j];//把其他数往后移动一格
		}
		ans[id]=a[i];//最后把数放进去
	}
	for(int i=1;i<=m;i++) cout<<ans[i]<<" ";
	return 0;
}

综上，这一题用上面的任意一种方法（除了后三种）就能过啦！