自动搬运

查看原文

来自洛谷，原作者为

	c60521c AFO

搬运于2025-08-24 21:23:09，当前版本为作者最后更新于2021-02-03 13:07:00，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题解

2021第一篇题解

引言

这道题很明显是一个树形结构但在看完标签后发现还有贪心，于是就想到了这样的方法 。

思路

1. 不用从根节点往下dfs每条线。
2. 可以从叶子结点往上爬，一直爬到根节点。
3. 将每条线上的信号衰减值累加，与初始信号强度比较。
4. 若累加值小于初始信号长度则不用安放，大于等于时ans++ 。

注意

特判点：

if(mx >= len)
	printf("No solution.\n");

说明：
当衰减值和初始强度相等时信号最后到达时会衰减为0，接收不到。

样例说明！

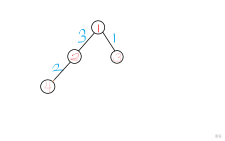
样例：
4
2 2 3 3 1
2 1 3 4 2
1 1 1
1 2 2
4

2 2 3 3 1
根节点有两个子节相连，分别为2和3，与之对应的信号衰减值为3和1。
2 1 3 4 2
节点2有两个节点相连，一个根节点另一个为四号节点，信号衰减值为3和2。
1 1 1
三号节点有一个节点相邻，衰减值为1，相连节点即为根节点 。
1 2 2
四号节点有一个节点相连，即为二号节点，衰减值为2 。
4
最后输入的是初始强度。

核心代码

1、用vector来存而不是直接int

vector<int> g[20005], d[20005];

2、从叶节点往上找到根节点过程中的信号衰减值综合与信号强度比较

void dfs(int x, int fa)
{//搜索结点x，其父结点为fa
	for(int i = 0; i <= g[x].size(); i++)
	{//枚举所有和结点x的相连的结点
		int y = g[x][i];
		if(y != fa) //只要该结点非父结点
		{
			p[y] = d[x][i]; //记录第y个点及其父结点连边的权重
			dfs(y, x);
			dis[x] = max(dis[x], dis[y] + d[x][i]);
		}
	}
	if(dis[x] + p[x] >= len)
	{
		ans++;
		dis[x] = 0;
	}
}

3、//有向图 v为i的临界顶点，push到g中

g[i].push_back(v);
d[i].push_back(w);
mx = max(mx, w);//存最大边长 w边长

接下来就是 AC Code

#include<cstdio>
#include<vector>
#include<cmath>
#include<iostream>
#include<algorithm> 
using namespace std;

vector<int> g[20005], d[20005];
int n, dis[20005], p[20005], ans, len;

void dfs(int x, int fa)
{//搜索结点x，其父结点为fa
	for(int i = 0; i < g[x].size(); i++)
	{//枚举所有和结点x的相连的结点
		int y = g[x][i];
		if(y != fa) //只要该结点非父结点
		{
			p[y] = d[x][i]; //记录第y个点及其父结点连边的权重
			dfs(y, x);
			dis[x] = max(dis[x], dis[y] + d[x][i]);
		}
	}
	if(dis[x] + p[x] >= len)
	{
		ans++;
		dis[x] = 0;
	}
}

int main()
{
	scanf("%d", &n);
	int mx = 0, v, w;//mx所有边最大边长 
	for(int i = 1; i <= n; i++)
	{
		int m;
		scanf("%d", &m);
		for(int j = 1; j <= m; j++)
		{
			scanf("%d%d", &v, &w);
			g[i].push_back(v);//有向图 v为i的临界顶点，push到g中 
			d[i].push_back(w);
			mx = max(mx, w);//存最大边长 w边长 
		}
	}
	scanf("%d", &len);
	dfs(1, 0); //结点1表示服务器
	if(mx >= len) //若边的最大损耗会超过信号初始强度则无解 
		printf("No solution.\n");
	else printf("%d\n", ans);
	
	return 0;
}    

完美结束。留个赞吧。