自动搬运

查看原文

来自洛谷，原作者为

	TimSwn090306 你说的对，但是区间LCA是相邻点对LCA中深度最浅的点

搬运于2025-08-24 23:16:35，当前版本为作者最后更新于2025-05-24 22:39:58，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

Description

初始有 $n$ 把军刀和 $m$ 个敌人，军刀有属性 $a,b,cost$，敌人有属性 $c,d,profit$。军刀 $i$ 能杀死敌人 $j$ 当且仅当 $a_i\ge c_j ,b_i\ge d_j$。你需要选出若干军刀和若干敌人，使得每一个选出的敌人都可以被至少一把选出的军刀杀死，并最大化选出的敌人的 $profit$ 之和减去选出的军刀的 $cost$ 之和。

数据范围：$n,m\le 10^6,a,b,c,d,cost,profit\le 10^9$。

Solution

把军刀和敌人放到二维平面上，对于选定的若干军刀，有贡献的敌人呈阶梯状（如下图）。

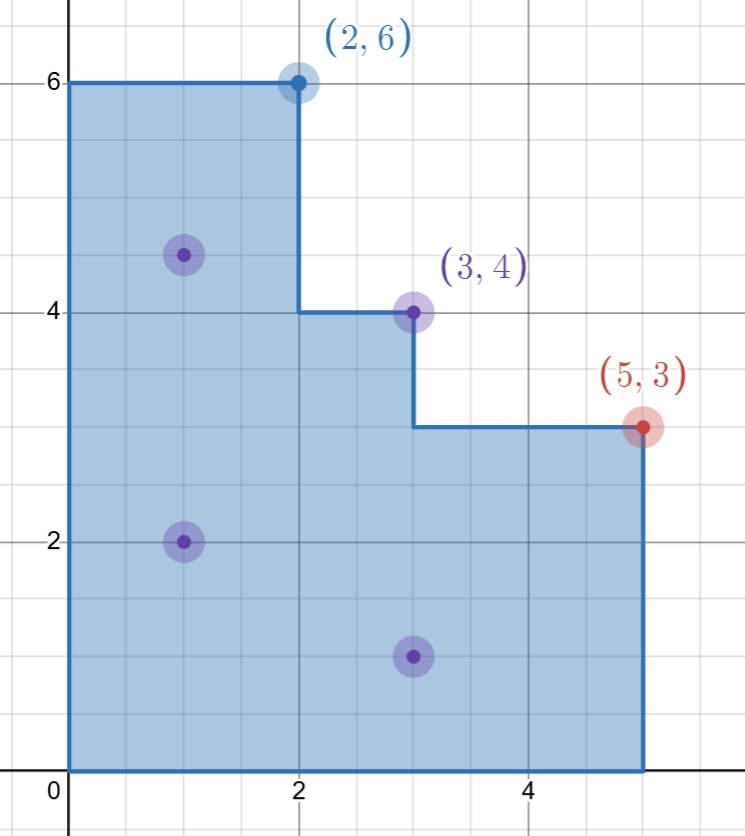
将所有点按 $y$ 排序，设 $f_i$ 表示考虑前 $i$ 把军刀，钦定第 $i$ 把必选的最大收益（$\sum profit-\sum cost$）。则有 $f_i=\max (f_j+w(j,i))-cost_i$，其中 $w(j,i)$ 表示上一把军刀为 $j$，新增一把军刀为 $i$ 的 $\sum profit$ 增量。简单实现可以做到 $O(n^2)\thicksim O(n^3)$，无法通过此题，需要优化。

注意到计算 $w(j,i)$ 时产生贡献的敌人的范围是一个 $([1,x_i],[y_j,y_i])$ 的矩形（如下图）。注意：若 $x_j<x_i$，转移本身是不优的，因为军刀之间存在偏序关系不优。同时 $j$ 到 $i$ 的转移的 $w(j,i)$ 也不是上述矩形，计算出来是小于真实值的，但又因为这个转移本身是不优的，故不用考虑该情况。形式化的讲，$w_{real}(j,i)\ge w(j,i),f_j+w_{real}(j,i)\le f_i \longrightarrow f_j+w(j,i)\le f_i$。

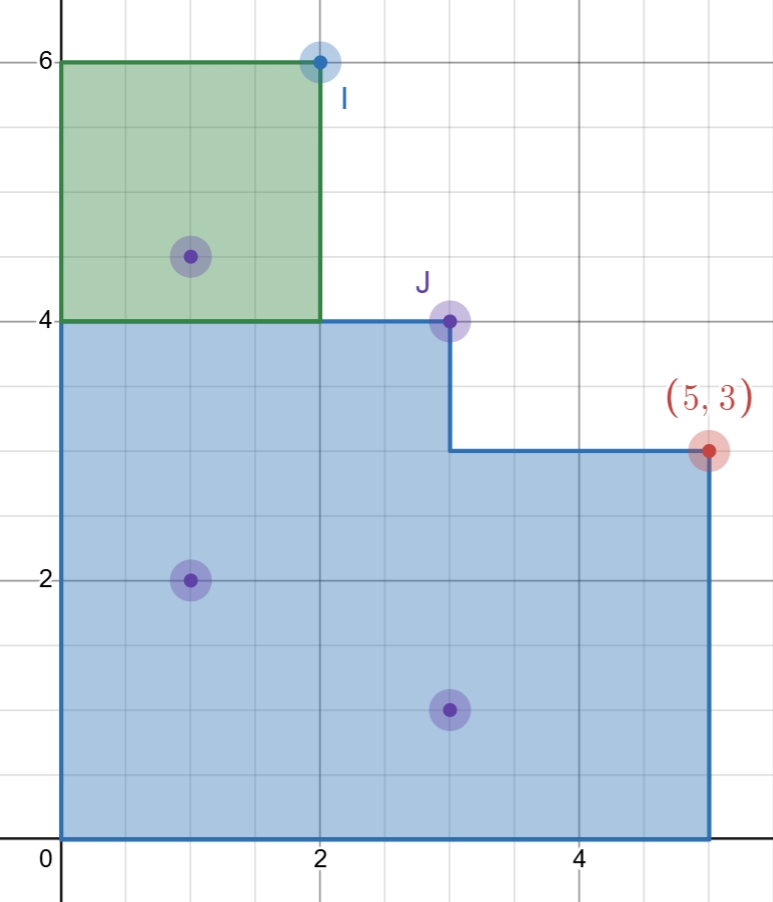
发现 $w(j,i)$ 和 $x_j$ 半毛钱关系没有，所以对于所有 $y$ 坐标相等的军刀，我只关心里面 $f$ 值最大的那一个，设 $l_i$ 表示 $y$ 坐标为 $i$ 的军刀里的 $f$ 最大值。

仍是从下到上枚举纵坐标 $y$，设 $p_i$ 表示若新增军刀坐标为 $(i,y)$，$cost$ 为 $0$，其 $f$ 值是多少，具体的，$p_i=\max_{j\in[1,y-1]}(l_j+sum([1,i],[j,y]))$，其中 $sum([sx,ex],[sy,ey])$ 表示矩形内敌人的 $profit$ 之和。$f_i=p_{x_i}-cost_i$。

尝试维护 $p$。不难发现新增第 $i$ 个敌人对 $p$ 的影响是 $[x_i,10^9]$ 区间加 $profit_i$，新增第 $i$ 个军刀对 $p$ 的影响是 $[1,10^9]$ 全局对 $f_i$ 取 $\max$。区间加，全局取 $\max$，单点查，线段树容易维护。

时间复杂度 $O(n\log n)$。

Code

#include <bits/stdc++.h>
#define ll long long
using namespace std;

const int maxn=2e6+5;
const ll INF=1e16;

int n,m,tot,b[maxn];
struct node{
	int type,x,y,c;
	inline bool operator < (node tmp) const{
		if (y!=tmp.y) return y<tmp.y;
		if (x!=tmp.x) return x<tmp.x;
		if (type!=tmp.type) return type<tmp.type;
		return c<tmp.c;
	}
}s[maxn];

namespace SGT{
	#define lc(rt) ((rt)<<1)
	#define rc(rt) ((rt)<<1|1)
	const int maxc=(maxn<<2);
	ll add[maxc],getmax[maxc];
	inline void lazy_add(int rt,ll k){
		add[rt]+=k;
	}
	inline void lazy_max(int rt,ll k){
		getmax[rt]=max(getmax[rt],k-add[rt]);
	}
	inline void pushdown(int rt){
		if (getmax[rt]){
			lazy_max(lc(rt),getmax[rt]);
			lazy_max(rc(rt),getmax[rt]);
			getmax[rt]=0;
		}
		if (add[rt]){
			lazy_add(lc(rt),add[rt]);
			lazy_add(rc(rt),add[rt]);
			add[rt]=0;
		}
	}
	inline void update_add(int rt,int l,int r,int ql,int qr,ll k){
		if (l>=ql && r<=qr){
			lazy_add(rt,k);
			return ;
		}
		pushdown(rt);
		int mid=(l+r)>>1;
		if (ql<=mid) update_add(lc(rt),l,mid,ql,qr,k);
		if (qr>mid) update_add(rc(rt),mid+1,r,ql,qr,k);
	}
	inline void update_max(int rt,int l,int r,int ql,int qr,ll k){
		if (l>=ql && r<=qr){
			lazy_max(rt,k);
			return ;
		}
		pushdown(rt);
		int mid=(l+r)>>1;
		if (ql<=mid) update_max(lc(rt),l,mid,ql,qr,k);
		if (qr>mid) update_max(rc(rt),mid+1,r,ql,qr,k);
	}
	inline ll query(int rt,int l,int r,int p){
		if (l==r){
			return max(0ll,getmax[rt])+add[rt];
		}
		pushdown(rt);
		int mid=(l+r)>>1;
		if (p<=mid) return query(lc(rt),l,mid,p);
		else return query(rc(rt),mid+1,r,p);
	}
}

ll f[maxn];

inline int rd(){
	int x=0; char ch=getchar();
	while (ch<'0' || ch>'9') ch=getchar();
	while (ch>='0' && ch<='9'){
		x=(x<<3)+(x<<1)+(ch-'0');
		ch=getchar();
	}
	return x;
} 

int main(){
	n=rd(),m=rd();
	for (int i=1;i<=n;i++) s[i].x=rd(),s[i].y=rd(),s[i].c=rd(),s[i].type=-1;
	for (int i=1;i<=m;i++) s[i+n].x=rd(),s[i+n].y=rd(),s[i+n].c=rd(),s[i+n].type=+1;
	
	for (int i=1;i<=n+m;i++) b[++tot]=s[i].x;
	sort(b+1,b+tot+1);
	tot=unique(b+1,b+tot+1)-b-1;
	for (int i=1;i<=n+m;i++) s[i].x=lower_bound(b+1,b+tot+1,s[i].x)-b;
	
	sort(s+1,s+n+m+1);
	memset(SGT::getmax,-0x3f,sizeof(SGT::getmax));
	
	for (int i=1;i<=n+m;i++){
		int j=i;
		while (j<=n+m && s[j].y==s[i].y) j++;
		for (int k=i;k<j;k++){
			if (s[k].type==+1){
				SGT::update_add(1,1,tot,s[k].x,tot,s[k].c);
			}
		}
		ll maxx=-INF;
		for (int k=i;k<j;k++){
			if (s[k].type==-1){
				f[k]=SGT::query(1,1,tot,s[k].x)-s[k].c;
				maxx=max(maxx,f[k]);
			}
		}
		SGT::update_max(1,1,tot,1,tot,maxx);
		
		i=j-1;
	}
	
	ll ans=-INF;
	for (int i=1;i<=n+m;i++) ans=max(ans,f[i]);
	
	printf("%lld\n",ans);
	
	return 0;
}