自动搬运

查看原文

来自洛谷，原作者为

	Iniaugoty 我一定会进盐中校队！！！！！11111

搬运于2025-08-24 23:16:22，当前版本为作者最后更新于2025-05-19 08:44:43，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

如何苏瞳速通 APIO 2025 Ag？？？很难不注意到只有 T3 是可做题，考虑把它过掉！

考虑 $n = 2$ 的情况，显然当且仅当两直线垂直时最优。

考虑 $n = 3$ 的情况，显然答案会是一个平角，否则会出现四条不共线的直线。特别地，当有两条直线垂直时能取到：它们之间夹一个直角，而第三条线与它们产生一对互余的角。不过不是仅当，但这并不重要。

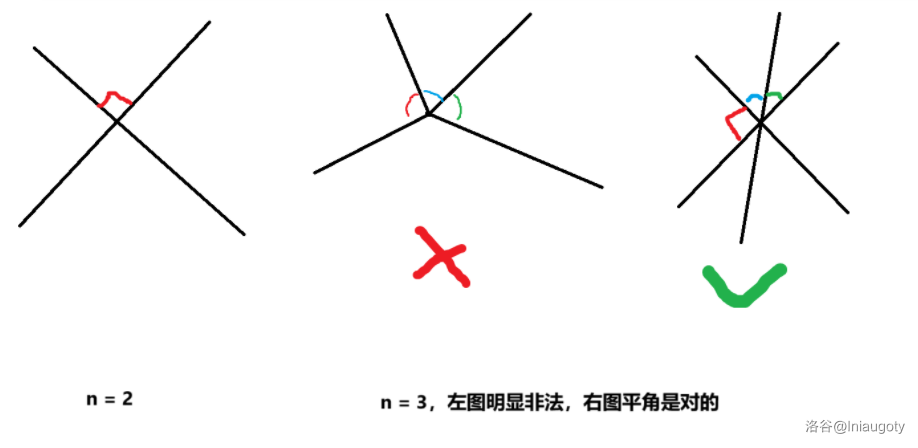
以上是两个基本的情形，下面将利用她们进行推广。

很难不发现最优解总是，直线两两垂直的配对起来（当然 $n$ 为奇数时会有一个多出来的）。

如果你发现不了的话，考虑归纳 / 增量法构造。$n = 2, 3$ 时我们已经会了，利用 $n = 2k$ 时的最优解推出 $n = 2k + 1, 2k + 2$ 的。首先考虑加入第 $2k + 1$ 条直线，出现了 $k$ 个 $n = 3$ 的情形，发现随便加（甚至跟已有的重合）都行；再加入第 $2k + 2$ 条直线，出现了 $k$ 个 $n = 3$ 的情形与 $1$ 个 $n = 2$，前者没啥要求，后者只需要保持使其与第 $2k + 1$ 条直线垂直即可。

那么有一个 naive 的想法是直接 $(i, i + \lfloor \frac n 2 \rfloor)$ 配对，但这是错的。问题出在哪，发现题目要求每一步之后值都不降，这个东西随便手玩一下就能 hack 掉。

如图，直接让 3 来迁就 1 得到与其垂直的 3' 的话，它与 2 和 4 的夹角明显会变小，而这个减小的程度超过了与 1 夹角的增加。

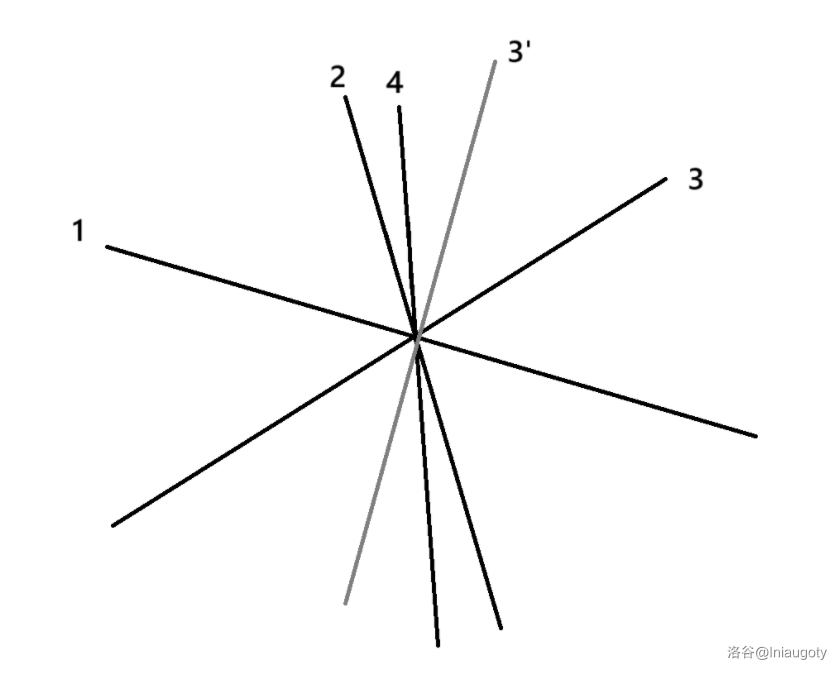
考虑大胆地将 $n$ 条直线排序一下，再 $(i, i + \lfloor \frac n 2 \rfloor)$ 配对。然后你发现这甚至是对的。

如果是赛时，几乎就不用管它了，我们已经完成了 Ag 中最难的一步！

考虑这个为什么是对的。对于已经配对好的直线来讲，别的不管怎么动贡献肯定都是直角，是没有影响的，因此忽略掉她们。注意到，从 $i$ 到 $\lfloor \frac n 2 \rfloor$ 之间的直线的数量（当然，只考虑剩下来的没被忽略掉的），与 $i + \lfloor \frac n 2 \rfloor$ 到 $n$ 之间的直线的数量，几乎是一样的，取决于 $n$ 的奇偶性最多相差 $1$。

考虑 $i + \lfloor \frac n 2 \rfloor$ 转动带来的变化，设其转动的锐角为 $\delta$。注意到那两部分间必然存在一部分，到 $i + \lfloor \frac n 2 \rfloor$ 的角度全部增加，且增加了 $\delta$；而另一部分中有增有减，并且变化的幅度都不超过 $\delta$。由于数量相差不超过 $1$，以及 ，$i + \lfloor \frac n 2 \rfloor$ 本身的增加，整体上是不减的。

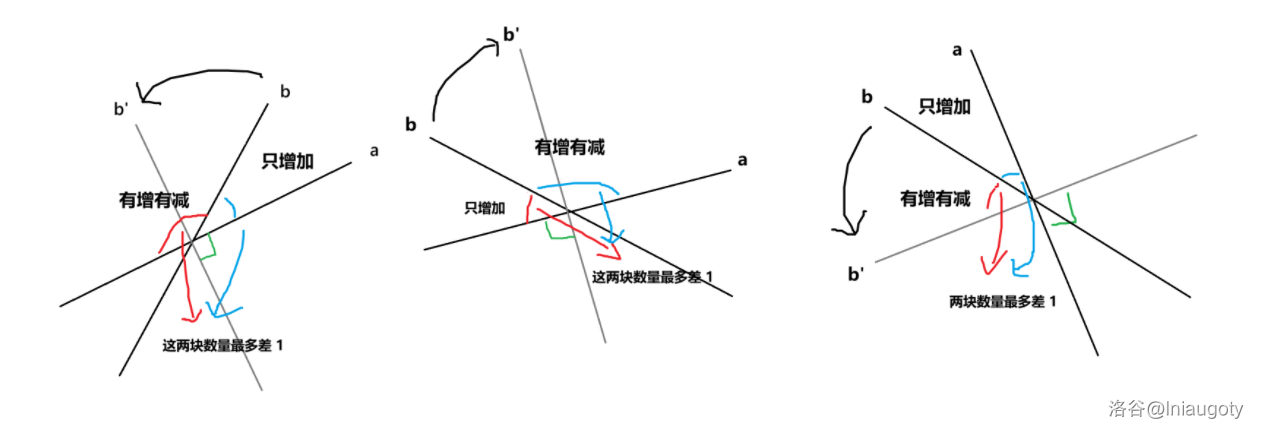
如上图是几种情况。

const int N = 1e5 + 5;
const int rt = 2.5e4, m = 5e4;
int a[N], p[N];
bool cmp(int x, int y) { return a[x] < a[y]; }
void energy(int n, vector<int> v) {
  F(i, 0, n - 1) a[i] = v[i], p[i] = i;
  sort(p, p + n, cmp);
  F(i, 1, n >> 1) {
    int x = p[i - 1], y = p[i - 1 + (n >> 1)];
    rotate({y}, ((v[x] + rt - v[y]) % m + m) % m);
  }
}

操作数是恰好的 $\lfloor \frac n 2 \rfloor$，而出题人的限制给到了足足 $2 \times 10 ^ 6$，哈哈哈，真幽默呀。

我是 xst 粉丝，建议降黄，嘟嘟嘟。