自动搬运

查看原文

来自洛谷，原作者为

	itzxianfish 握握手，握握双手

搬运于2025-08-24 23:16:17，当前版本为作者最后更新于2025-05-24 11:03:24，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

前言

本蒟蒻当时在比赛现场猜测到了这道题跟凸包有关系，但是奈何当时根本不会求凸包，遂遗憾抛弃本题 QAQ。

后来学了 Graham 算法和搓了几道板子之后回想起来这道题，结果用 Graham 调了一个下午，疯狂保龄。

因为直到我 AC 这道题的时候，仍然没有题解，于是在大佬的帮助以及各方面调查下，加上现学了一手 Andrew 算法，然后一发了本题，于是写此篇题解以提供帮助和警示后人。

题解

题意

判断简单非退化多边形上是否存在有限个 $P$，$Q$ 两点，使得线段 $PQ$ 与多边形不是仅交于 $P$，$Q$ 两点。

第一个比较有意思的点就是，这里的的多边形指整个多边形区域，所以你的线段是不能穿过内部的，参考测试样例的第二个点。

4
1 1
-1 1
-1 -1
1 -1

显然，这是一个正方形。

但是如果你误解了题意，可能就会认为线段从内部穿过是没问题的，于是浪费时间在思考这件事上面。

与凸包的联系

在题目中给的图比划一下，大致猜测到棱堡的几何性质会与多边形的凹凸有关系。

这里有一个结论：如果一个简单非退化多边形是棱堡，则原多边形不存在任意一条边在凸包上。

简单证明如下。

我们假设存在一个棱堡的某一条边在多边形点集形成的凸包上。

那么根据凸包的定义，结合下图。

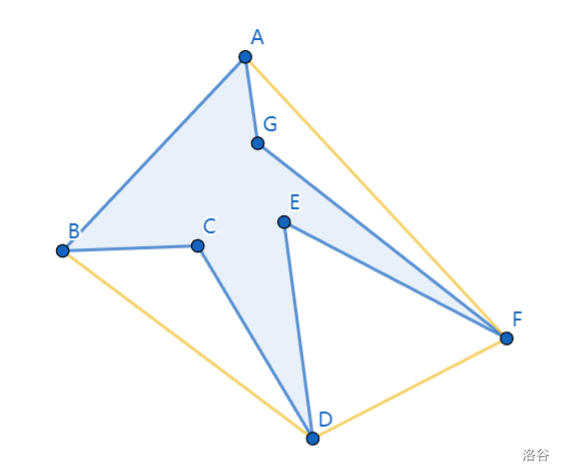
其中黄色加上线段 $AB$ 是这个假设棱堡的凸包，蓝色线段及其所围区域是假设的棱堡。

由于 $AB$ 是凸包上的边，我们容易发现：任意除 $A$，$B$ 以外的顶点必然仅处于线段 $AB$ 的单侧。

但是此时我们如果取线段 $AB$ 上的某一点 $P$（不包含端点），要寻找另一点 $Q$ 形成火力直射时，由于顶点全部在线段 $AB$ 的一侧，使得棱堡形成的多边形区域也是集中在这一侧，导致线段 $PQ$ 必然会穿过棱堡的内部区域形成火力盲区（上述解释可能有些抽象，建议自己画图加深理解）。

我们发现 $P$ 的选取在 $AB$ 上是任意的，于是会有无穷的 $P$ 形成火力盲区，与棱堡定义不符，于是原假设的多边形不是棱堡。

到这里，我们就简单的证明了结论：如果一个简单非退化多边形是棱堡，则原多边形不存在任意一条边在凸包上。

凸包算法

我们常见的凸包算法是 Graham 算法和 Andrew 算法，不熟悉的可以先去写一下模板题：P2742 [USACO5.1] 圈奶牛Fencing the Cows /【模板】二维凸包。

但是正如我的前言所说，我用 Graham 算法调了一个下午，所以我们这里解释一下 Graham 算法在这题里面的坑点。

Graham 算法坑点

我们知道 Graham 算法是基于极角排序的，在极角相同，即共线时，我们的第二关键字会选择向量模长。

但这个时候就会有个问题：这个共线点，他到底是不是在凸包上？

如图。

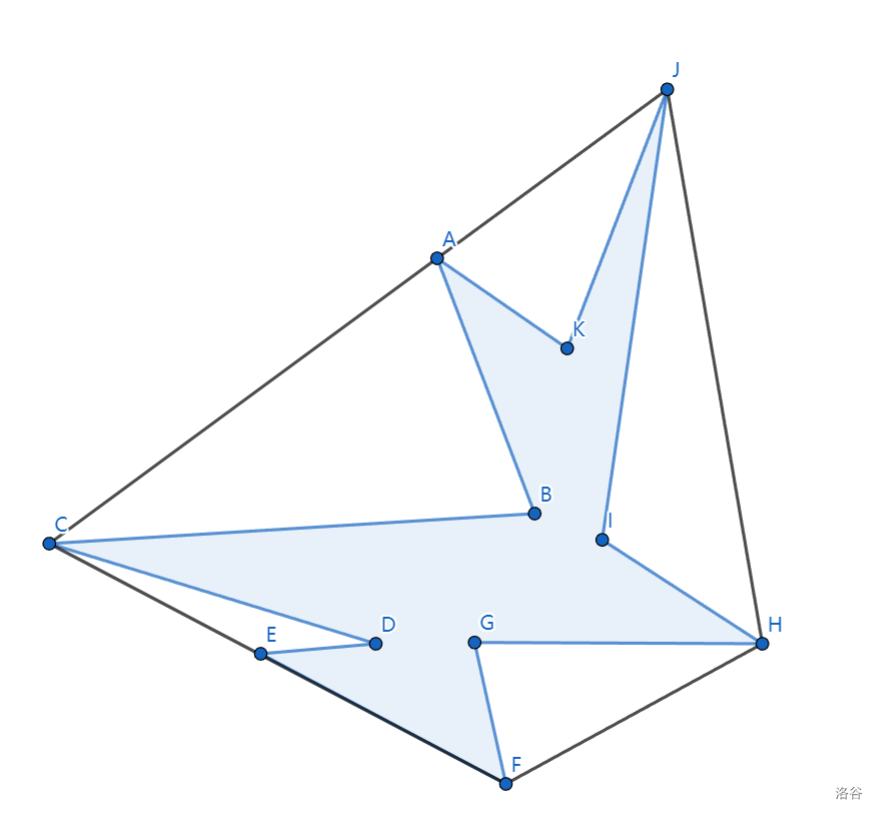
有 $J$，$A$，$C$ 和 $C$，$E$，$F$ 两组三点共线，根据 Graham 算法，这里我们的基准点应该是 $F$，我们关注聚焦在线段 $EF$，因为其他的点我们在出栈的时候，把 $\vec{a} \times \vec{b} \le 0$ 改成 $\vec{a} \times \vec{b} < 0$ 就好了。

现在考虑 $C$，$E$，$F$ 这一组，假设我们排序的第二关键字是模长更小排前面那就会先走 $E$，再走 $C$，显然这个时候 $E$ 会被提前出栈，导致凸包点集不包含 $E$ 这个点，但是反过来，如果第二关键字是模长更大，就是先走 $C$，再走 $E$，此时又会正常包含 $E$。

上面的分析其实聚焦于一个关键点就是：极角排序使用模长作为第二关键字处理共线情况会存在不确定性。

再看 Andrew 算法，排序只需要关注坐标的情况，涉及到共线的操作只有出栈，所以此时我们只需要略微调整模板，使得最终栈内能存在共线点即可。

综上，本题我们采用 Andrew 算法计算凸包。

注意事项

我们需要的是点集中所有在凸包上的点，如同前文所说，要把 $\vec{a} \times \vec{b} \le 0$ 改成 $\vec{a} \times \vec{b} < 0$ 确保获取所有点。

AC Code

含注释。

#include <cstdio>
#include <algorithm>
#include <set>
#define int long long   // 十年 IO 一场空，不开 ________ 见祖宗
using namespace std;

const int MAXN = 100020;
int t, n, top, used[MAXN], stk[MAXN];

// 快读
inline int read() {
    int x = 0, f = 1; char c = getchar();
    while (c < '0' || c > '9') { if (c == '-') f = -1; c = getchar(); }
    while (c >= '0' && c <= '9') { x = (x << 1) + (x << 3) + (c ^ '0'); c = getchar(); }
    return x * f;
}

// 向量，含叉乘
struct Vector {
    int x, y;
    Vector(int __x = 0, int __y = 0) : x(__x), y(__y) {}
    int cross(const Vector& o) const { return x * o.y - y * o.x; }
};

// 点，重载减法获取向量，重载小于用于排序和 set
struct Point {
    int x, y;
    Point(int __x = 0, int __y = 0) : x(__x), y(__y) {}
    Vector operator- (const Point& o) const { return Vector(x - o.x, y - o.y); }
    bool operator< (const Point& o) const { return x == o.x ? y < o.y : x < o.x; }
} a[MAXN], b[MAXN];

// 凸包点集
set< Point > s;

// Andrew 算法
inline void Andrew() {
    // 初始化
    s.clear();
    top = 0;
    for (int i = 1; i <= n; i++)
        used[i] = 0;
    
    sort(a + 1, a + n + 1);
    stk[++top] = 1;
    for (int i = 2; i <= n; i++) {
        while (top >= 2) {
            Vector v1 = a[stk[top]] - a[stk[top - 1]];
            Vector v2 = a[i] - a[stk[top]];
            if (v1.cross(v2) < 0)   // 注意符号
                used[stk[top--]] = 0;
            else
                break;
        }
        used[i] = 1;
        stk[++top] = i;
    }

    int t = top;
    for (int i = n - 1; i; i--) {
        if (!used[i]) {
            while (top > t) {
                Vector v1 = a[stk[top]] - a[stk[top - 1]];
                Vector v2 = a[i] - a[stk[top]];
                if (v1.cross(v2) < 0)   // 注意符号
                    used[stk[top--]] = 0;
                else
                    break;
            }
            used[i] = 1;
            stk[++top] = i;
        }
    }

    // 存入 set
    for (int i = 1; i < top; i++)
        s.insert(a[stk[i]]);
}

signed main() {
    t = read();
    while (t--) {
        n = read();
        for (int i = 1; i <= n; i++) {
            a[i].x = read(), a[i].y = read();
            b[i] = a[i];    // 保存原顺序
        }

        Andrew();

        bool flag = true;
        for (int i = 1; i <= n; i++)
            if (s.count(b[i]) && s.count(b[i % n + 1])) // 题目已经保证输入顺序，直接判断相邻两个元素即可
                flag = false;
        puts(flag ? "YES" : "NO");
    }
    return 0;
}

后记

代码调了一个下午真的红温了，为了避免后人红温，留此解 awa。

关于使用 set，相信各位巨佬应该有时间更优的手段可供替换。

码字不易 TAT。

最后，管理员大大求过求过求过求过求过求过。