自动搬运

查看原文

来自洛谷，原作者为

	隔壁泞2的如心 AFO|以某种事物作为代价，以某种代价作为契机……？

搬运于2025-08-24 23:15:58，当前版本为作者最后更新于2025-05-17 02:56:23，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

集训队互测出现大量不可做计数 我被吓死了 余生在阿巴阿巴中度过……

首先你可以发现！想要解决原问题我们只需要将树进行长链剖分然后贪心地选前 $k$ 长的链即可。你可以用你喜欢的方式证明它，我用的是类似 Slope Trick 的推法（

那么要想解决计数版问题，我们可以考虑给定长剖完的链长集合后，有多少棵树可以被剖成给定的集合。首先我们要规范一下长剖的过程，如果一个节点的多个儿子深度相等，我们要选择 链底节点编号最小 的儿子。那么我们就要考虑有多少棵树，满足它被长剖之后被分为了 $h$ 条链，并且将这些链按链底节点编号排序后，第 $i$ 个链长度为 $h_i$。

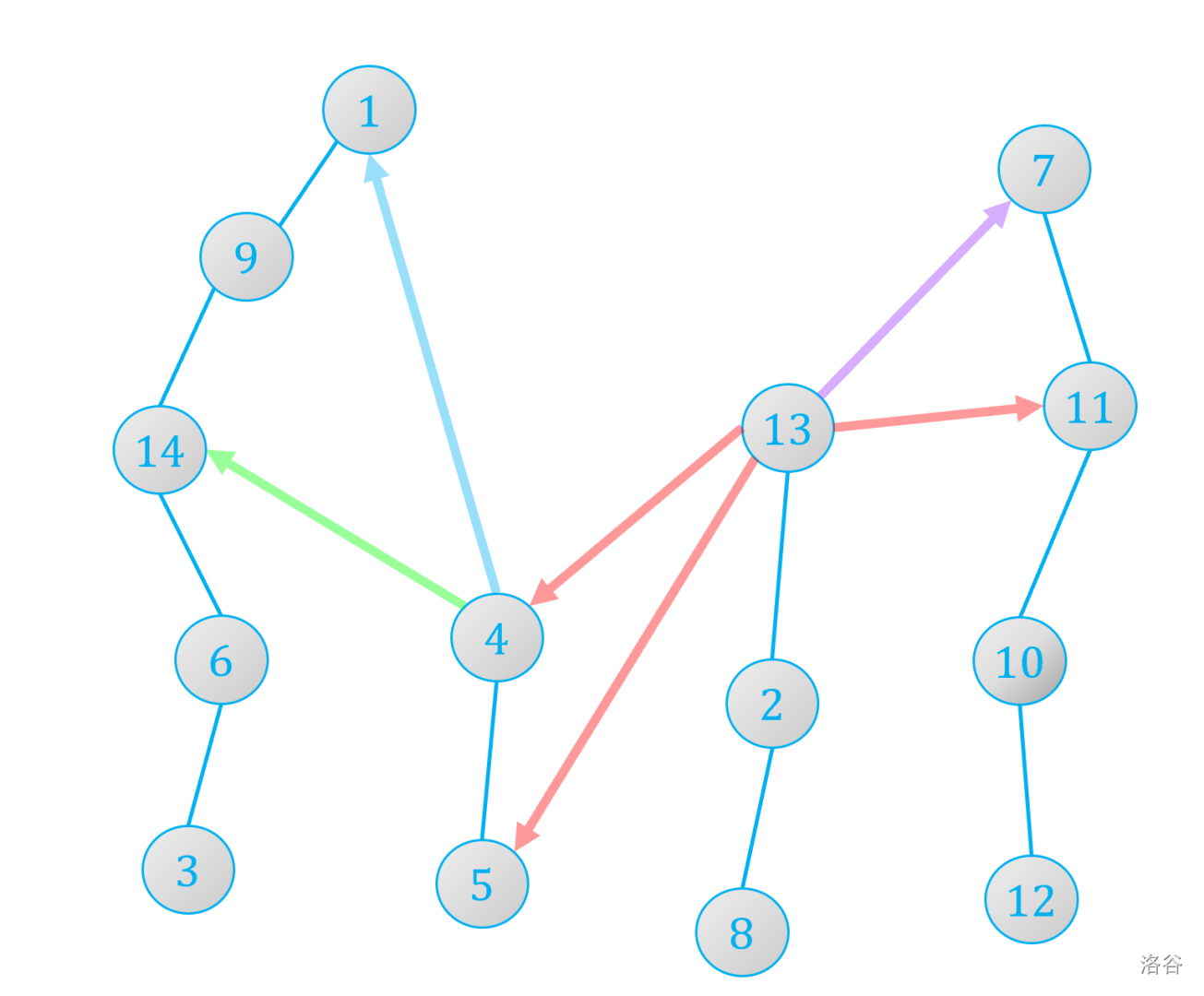
如图所示，我们只需要为每个不为 $1$ 的链顶选一个父亲即可。首先每个节点的父亲都必须比自己高，不然就会违反长剖中的深度限制。如图中蓝色的连接合法，红色的连接不合法。但还要额外注意一点！如果某个点的父亲只比自己高 $1$ 条边，那么这条边一定是往左连的，不然就会违反长剖中的链底编号限制。如图中绿色的连接合法，紫色的连接不合法。当然还要乘上分配编号的方案数，不过分配编号的方案很独立，在任何情况下都是 $\dfrac{(n-1)!}{h!}$。

推到这里之后，这题的关键部分就已经过去了。题目中的 $k$ 和 $m$ 限制其实就是指“集合中前 $k$ 长的链总长为 $m$”。而我们可以很容易地通过按长度从大到小/从小到大加入链、记录已加入的链数和链的总长来 dp。

不过，本题的 dp 其实比较复杂，想要的答案和 dp 过程之间的相性并不好。“前 $k$ 长的链的总长”在 dp 中只是中间值，所以你需要用正反两个方向的 dp 数组才能将答案按照中间值分类——当然也许可以不用，dp 题最好玩的地方就是你很可能被一些不难的地方卡住……

最后需要注意答案矩阵的最后一列和别的列不太一样，由于这一列的 $m=n$，所有的链都已被选，你可能需要对它做一下前缀和（

#include<bits/stdc++.h>
#define int long long
#define FSIZ 407693
#define add(a,b) (a+=(b),a>=mod?a-=mod:0)
#define neg(x) ((x)&1?mod-1:1)
#define Q(a,b) C((a)+(b)-1,(b)-1)
#define cond(a,b)((a)?(b):0)
using namespace std;
int fac[FSIZ],ifac[FSIZ],inv[FSIZ];
int n,mod,dp1[304][304][304],dp2[304][304][304];
int C(int n1,int m1){
    if(m1<0||m1>n1)return 0;
    return fac[n1]*ifac[m1]%mod*ifac[n1-m1]%mod;
}
inline int qpow(int n1,int n2){
    int n3=n1,n4=1;
    while(n2){
        if(n2&1)n4*=n3,n4%=mod;
        n3*=n3,n3%=mod;n2>>=1;
    }return n4;
}
inline int mut(initializer_list<int> arg){
	int ret=1;
	for(auto i:arg)ret*=i,ret%=mod;
	return ret;
}
int res[304][304][304],ans[350][350];
signed main(){
    scanf("%lld%lld",&n,&mod);
    if(n==1){printf("1");return 0;}
    fac[0]=1;for(int i=1;i<=FSIZ-1;i++)fac[i]=fac[i-1]*i%mod;
    ifac[FSIZ-1]=qpow(fac[FSIZ-1],mod-2);for(int i=FSIZ-1;i>=1;i--)ifac[i-1]=ifac[i]*i%mod;
    inv[0]=0;for(int i=1;i<=FSIZ-1;i++)inv[i]=ifac[i]*fac[i-1]%mod;
    for(int i=0;i<=n;i++){
        res[i][0][0]=1;
        for(int j=1;j<=n-i;j++){
            for(int h=0;h<=j;h++){
                if(h>0)add(res[i][j][h],res[i][j-1][h-1]);
                add(res[i][j][h],res[i][j-1][h]*(i+h)%mod);
            }
        }
    }
    for(int i=n;i>=1;i--)dp1[i][1][i]=1;
    for(int i=n-1;i>=1;i--){
        for(int j=1;j<=n;j++){
            for(int h1=j+1;h1<=n;h1++){
                for(int h2=(i*h1)+(h1-j);h2<=n;h2++){
                    //printf("%lld %lld %lld %lld\n",i,j,h1,h2);
                    add(dp1[i][h1][h2],dp1[i+1][h1-j][h2-i*j]*res[h2-(i*h1)-(h1-j)][h1][h1-j]%mod);
                    
                }
            }
        }
        for(int h1=1;h1<=n;h1++){
            for(int h2=1;h2<=n;h2++){
                add(dp1[i][h1][h2],dp1[i+1][h1][h2]);
            }
        }
    }
    for(int i=1;i<n;i++)dp2[1][i][n]=fac[n-1]*ifac[i]%mod;
    for(int i=1;i<n;i++){
        for(int h1=1;h1<=n;h1++){
            for(int h2=h1*i;h2<=n;h2++){
                for(int j=1;h1-j>=0&&h2-i*j>=0;j++){
                    if(h2-i*h1-(h1-j)>=0)add(dp2[i+1][h1-j][h2-i*j],dp2[i][h1][h2]*res[h2-i*h1-(h1-j)][h1][h1-j]%mod);
                }
            }
        }
        for(int h1=1;h1<=n;h1++){
            for(int h2=1;h2<=n;h2++){
                add(dp2[i+1][h1][h2],dp2[i][h1][h2]);
            }
        }
    }
    for(int i=2;i<=n;i++){
        for(int j=1;j<=n;j++){
            for(int h1=1;h1<=n-j;h1++){
                for(int h2=h1*i;h2<=n-(i-1)*j;h2++){
                    for(int j2=1;j2<=j;j2++){
                        add(ans[h1+j2][h2+j2*(i-1)],dp1[i][h1][h2]*res[h2-h1-(i-1)*h1][h1+j][h1]%mod*dp2[i-1][h1+j][h2+(i-1)*j]%mod);
                    }
                }
            }
        }
    }
    for(int i=2;i<=n;i++){
        add(ans[1][i],dp2[i][1][i]);
    }
    for(int i=2;i<=n;i++){
        add(ans[i][n],ans[i-1][n]);
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            printf("%lld ",ans[i][j]);
        }
        printf("\n");
    }
}