自动搬运

查看原文

来自洛谷，原作者为

	CuteChat **

搬运于2025-08-24 23:15:47，当前版本为作者最后更新于2025-02-08 14:19:30，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题解

如果您并没有数位动态规划的基础，可以看看出题人写的烂笔记。

Subtask 1

$R_i$ 是 $10$ 的幂次减一，相当于行的限制不管用了，而列的限制就遵循列的限制进行计算即可，答案易得 $\displaystyle\prod(C_i+1)$。

Subtask 3

这里是一个数位动态规划模板，本质就是问你 $0\sim C_1$ 中，有多少个数字，满足任意的 $j$ 都满足第 $j$ 位小于等于 $R_j$。

这个只需要记录一个标记表示是否小于 $C_1$ 即可，从高到低位做，转移是显然的。

Subtask 4

这一步大概可以理解为 $m$ 个数位动态规划同时进行，所以直接先记录 $m$ 个标记，实际写代码的时候可以考虑状态压缩，用一个二进制数表示列标记的状态。

那么假定我们进行到了第 $i$ 行，就直接枚举当前这一行的数字是什么（而不是一个数位），直接检查是否满足这 $m$ 个标记的限制，并且直接转移即可。

时间复杂度是 $O(n 10^m 2^m)$，感觉比正解复杂，不推荐写。

Subtask 5

数位动态规划的本质就是用来优化枚举的数字的，既然内层又套了一层枚举，就继续用数位动态规划优化。

具体来说，流程是从上到下、从左往右的顺序填写每一个格子，结合轮廓线的思想，只维护当前这个格子所对应轮廓线上的标记状压值即可。

具体来说，整个算法的运行状况大约如图下所示（蓝色和绿色的就是轮廓线）：

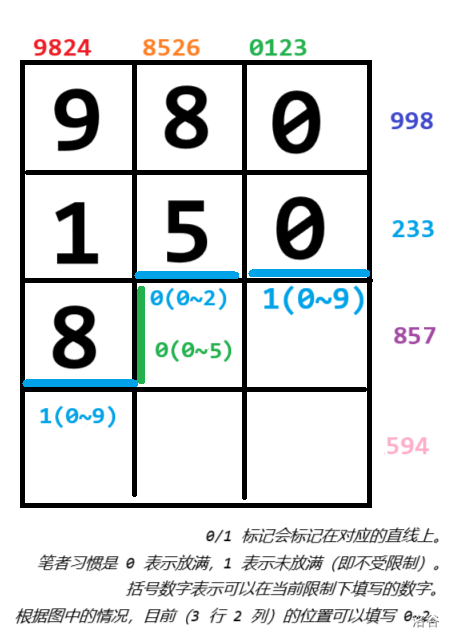
比如目前的格子，如果填写 $2$，那么当前这一行（绿色）的标记会改变为 $1$。而列（蓝色）的标记，如果仍然填写 $2$，那么标记不变。

转移后，第二列的蓝色轮廓线将会下降一格，备用于下一列的处理，绿色轮廓线将会右移一格，与正常的动态规划无异。

这一档很宽松，能保证不管常数有多大都能得到这一部分分。

Subtask 6, 7, 8

仔细分析 Subtask 5 的复杂度，发现是 $O(nm 2^m)$ 的。似乎能能得到 $100$ 分，但是实际上内部仍然是由一个枚举 $0\sim9$ 的数位的过程。带上两倍常数运算量大约为 $1.69\times10^{9}$，几乎过不了。

不过内部枚举 $0\sim9$ 的数位其实只有两种本质不同的数位，一种是会让至少一种标记不会更新，一种是都不会让标记更新的。

第一种显然只会有一个数，也就是目前标记状态的情况下可以填写的最大数位，转移不需要任何代价。

第二种显然就是所有小于这个最大数位的数位，这些数位的转移都是一样的，因为不管怎样比较都是小于，直接加上新转移的状态值与方案数的乘积即可。

这样就省去了 $10$ 倍的常数，由于空间不足以开 $18\times18\times2^{18}$ 的数组，所以使用滚动数组优化。

代码（正常写法）

#include <bits/stdc++.h>
using namespace std;

const int N = 18;
int n, m, dp[2][N][1 << N][2], r[N][N], c[N][N];

inline int stat(int i, int j, int lim, int llim) { // 获取正确的状态值，书写代码方便。
	if (i == n - 1 && j == m) return 1;
	if (j == m) return dp[(i + 1) & 1][0][lim][0];
	return dp[i & 1][j][lim][llim];
}

signed main() {
	ios::sync_with_stdio(0); cin.tie(0);
	cin >> n >> m;
	for (int i = 0; i < n; ++i) {
		long long x; cin >> x;
		for (int j = m - 1; j >= 0; --j) {
			r[i][j] = x % 10;
			x /= 10;
		}
	}
	for (int i = 0; i < m; ++i) {
		long long x; cin >> x;
		for (int j = n - 1; j >= 0; --j) {
			c[i][j] = x % 10;
			x /= 10;
		}
	}
	for (int i = n - 1; i >= 0; --i) {
		for (int j = m - 1; j >= 0; --j) {
			for (int lim = 0; lim < (1 << m); ++lim) {
				for (int llim = 0; llim <= 1; ++llim) {
					long long ans = 0;
					int d1 = (llim ? 9 : r[i][j]);
					int d2 = ((1 << j) & lim) ? 9 : c[j][i];
					int mind = min(d1, d2); // 计算出最大可以填的数位
					ans += stat(i, j + 1, (lim | (mind != c[j][i] ? (1 << j) : 0)), llim | (mind != r[i][j]));
					if (mind) ans += 1ll * mind * stat(i, j + 1, lim | (1 << j), 1); // 剩下的就是固定的转移，只要乘方案数即可
					dp[i & 1][j][lim][llim] = ans % 998244353;
				}
			}
		}
	}
	cout << dp[0][0][0][0] << "\n";
	return 0;
}

挑战最优解（标程写法）

1. 直接定义 $(i,n)$ 的下一个格子是 $(i+1,1)$，于是又可以滚动掉无用的一维，这样不仅可以省下一个长度 $18$ 的状态，还减少了时间常数。
2. 可以用定期取模。通过估算发现 $9^9 \times 998244353$ 很接近了 $64$ 位整数的范围，所以只需要在转移 $9$ 次后统一取模即可。
3. 循环的最后一层是枚举的是当前行的标记，这个循环直接展开即可。
4. 在第三步基础上去除一些冗余代码。以及其他的卡常。

这样写跑得飞起，轻轻松松卡近 $\text{250ms}$，虽然第二条卡常很抽象，但即使不用也能跑到大约 $\text{430ms}$。

#include <iostream>
#include <algorithm>
#define int long long
using namespace std;
const int N = 18, p = 998244353;
int n, m, dp[2][1 << N][2];
int r[N*N], c[N*N];

signed main() {
	cin >> n >> m;
	for (int i = 0; i < n; ++i) {
		long long x; cin >> x;
		for (int j = m - 1; j >= 0; --j) {
			r[i * m + j] = x % 10;
			x /= 10;
		}
	}
	for (int j = 0; j < m; ++j) {
		long long x; cin >> x;
		for (int i = n - 1; i >= 0; --i) {
			c[i * m + j] = x % 10;
			x /= 10;
		}
	}
	for (int lim = 0; lim < (1 << m); ++lim) {
		for (int llim = 0; llim <= 1; ++llim) {
			dp[(n * m) & 1][lim][llim] = 1;
		}
	}
	for (int id = n * m - 1; id >= 0; --id) { // 优化 1，需要注意判断列边界。
		for (int lim = 0; lim < (1 << m) ; ++lim) {
				// 循环展开，优化 3
				int mind = std::min((int)r[id], ((lim >> (id % m)) & 1) ? 9 : c[id]);
				dp[id & 1][lim][0] = 
					(dp[(id + 1) & 1][lim | (mind != c[id] ? (1 << (id % m)) : 0)][(id % m == m - 1 ? 0 : (mind != r[id]))] + 
					1ll * mind * dp[(id + 1) & 1][lim | (1 << (id % m))][(id % m == m - 1 ? 0 : 1)]);
				mind = ((lim >> (id % m)) & 1) ? 9 : c[id];
				dp[id & 1][lim][1] = 
					(dp[(id + 1) & 1][lim | (mind != c[id] ? (1 << (id % m)) : 0)][id % m != m - 1] + 
					1ll * mind * dp[(id + 1) & 1][lim | (1 << (id % m))][(id % m == m - 1 ? 0 : 1)]);
		}
		if (id % 9 == 0) { // 优化 2
			for (int lim = 0; lim < (1 << m); ++lim) {
				dp[id & 1][lim][0] %= p;
				dp[id & 1][lim][1] %= p;
			}
		}
	}
	cout << dp[0][0][0] % p; // 记得最后取模
	return 0;
}

闲话

如果您有什么特别厉害的正确做法比标程还要快很多，欢迎与出题人交流。

另外由于新的线路开通，为了修建 $\color{#f2a900}\dfrac{0}{6}\color{black}/\color{e4002b}\dfrac{1}{14}\color{black}/\color{862041}\dfrac{9}{4}\color{black}/\color{#665ec4}\dfrac{27}{9}$ 站的四线换乘我不知道需要多少世纪。