自动搬运

查看原文

来自洛谷，原作者为

	ARIS1_0 我们在逆境中绽放||go whk 8.24-9.30

搬运于2025-08-24 23:15:33，当前版本为作者最后更新于2025-07-16 20:19:40，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

感谢草八牛学长给我推荐的这道题，极大地增强了我的思维能力。以及代码能力。

首先我们可以把本题的仙人掌转化为一种比较通用的形态表示，我将其称之为“大菊花”。点 $1$ 的度数为 $n-1$，然后其挂着一堆独立的边或者一堆环，这些环全部都是三元环，形如 $\{1,a,b\}$。为什么不能是四元环五元环？发现我们其实很容易就可以缩减一个环的大小，例如我们现在有一个五元环：

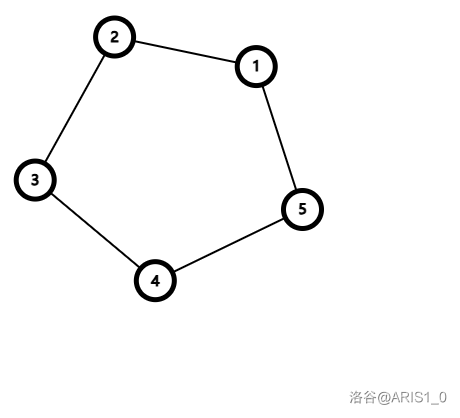
我们可以断开 $(3,4)$ 并连接上 $(1,3)$，你就可以发现它变成了一个三元环。随后我们再断开 $(4,5)$ 并连接 $(1,4)$，我们就成功将其变成了“大菊花”：

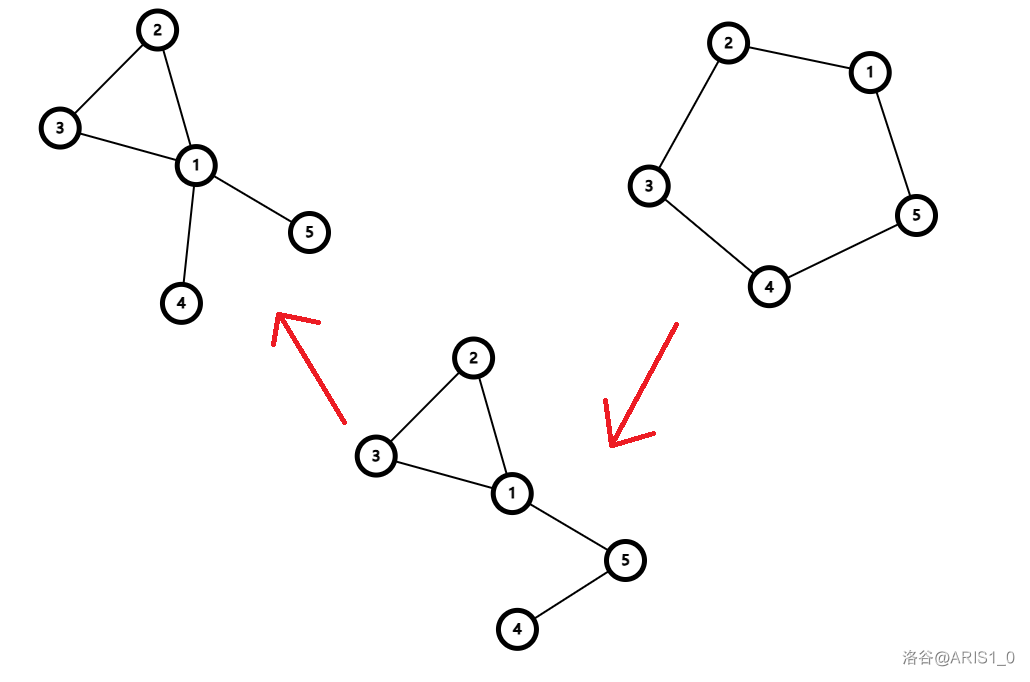
对于一个 $k$ 元环 $\{u_1,u_2,u_3,\dots,u_k\}$，我们只需要断开 $(u_1,u_k)$ 并连接 $(u_1,u_3)$，就会将其变成一个三元环拖着一条链。现在操作完后图中应该会剩下这么一些东西：连着 $1$ 的三元环，连着 $1$ 的单边，通过桥连着 $1$ 的三元环，通过三元环连着 $1$ 的三元环：

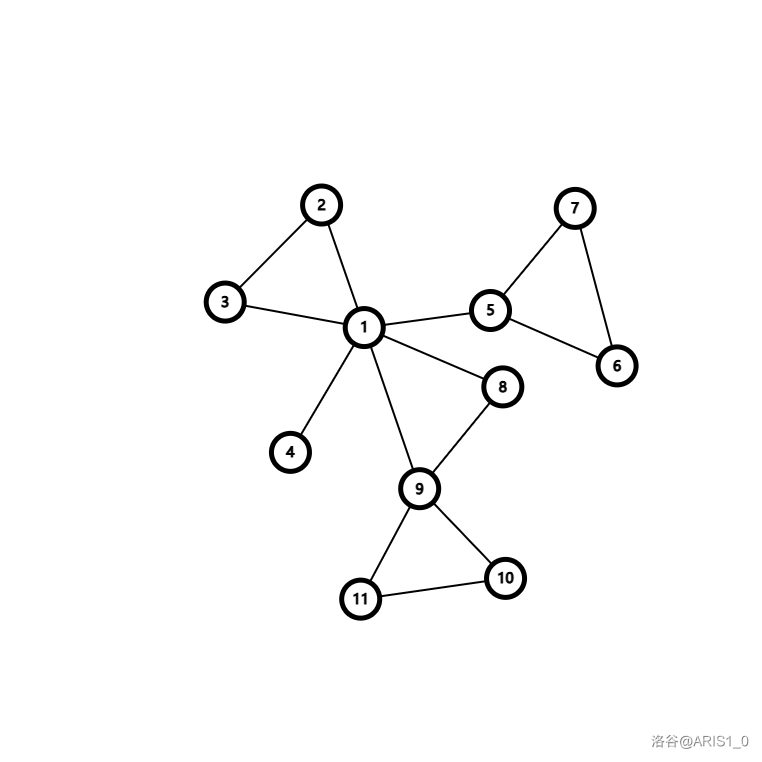
前两种情况就是我们想要的，后两者如何处理？对于通过桥连着 $1$ 的情况很好处理（若一个三元环 $\{u_1,u_2,u_3\}$ 通过桥 $(u_1,v)$ 连接至另一个三元环而不是直接连接 $1$，我们显然可以通过断开 $(u_1,v)$ 并连接 $(1,u_1)$ 转移过来）以图为例，我们断开 $(6,7)$，连接 $(1,6)$ 就转化成了一个三元环拖着一个链的形式，剩下的部分很好处理。我们接着来看三元连环的情况：

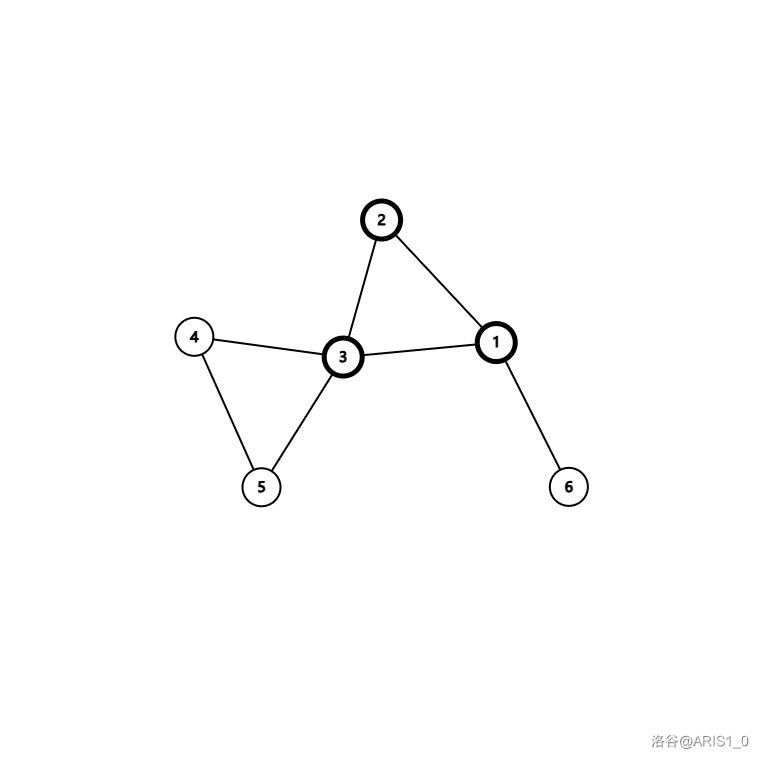
显然，我们一定会剩下一个连接着 $1$ 且度数为 $1$ 的点，否则是无解的。这种情况我们只需要把 $(2,3)$ 断开，连接 $(2,6)$，就可以转化成桥的情况。至此，所有情况转化完毕，这道题就做完了。

对于无解情况，当且仅当 $n$ 为奇数，$\frac{3(n-1)}{2}=m$ 且两颗仙人掌不同构时无解。理解这个式子不难，除去 $1$ 外的每个点都形成一个三元环，则两个点产生三条边的贡献。此时断边后会发现不论连哪个点都会导致破坏仙人掌的性质，这也是为什么上文提到的三元连环情况一定会存在一个连接着 $1$ 的且度数为 $1$ 的点。题目中的操作显然可逆，那么我们的两个仙人掌必定都能转化为同一个“大菊花”。题目转化为将两个仙人掌转化成同一个“大菊花”，剩下的就是操作次数的限制了。

注意到之前所说的三种情况中，第一二种情况的每次操作必定使得点 $1$ 的度数增加 $1$，第三种情况必定能通过一次操作转化为第二种情况，不增加点 $1$ 度数。则总操作次数为 $O(n)$。可以通过本题。

当然，两个仙人掌转化成“大菊花”后肯定会出现编号不同的情况，我们利用单条链转编号就行了，容易看出这样是整体 $O(n)$ 的。

代码在此。

内含少量注释，看不懂的可以评论区咨询。因为是学长一步一步讲的所以可能和学长代码比较相似。

拜谢草八牛。