自动搬运

查看原文

来自洛谷，原作者为

	chenly8128 God helps those who help themselves.

搬运于2025-08-24 23:15:12，当前版本为作者最后更新于2025-05-01 21:46:14，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

其实这道题不需要上数据结构。

我的方法是：预处理，然后分类、拆分。根本途径是通过倍增求解。

预处理

通过两次深搜，分别求出：

1. 深度，倍增跳表，向下的最长链，向下的次长链，向下最长链的儿子编号。（最长链和次长链要求不能有重复的边，但是长度可以相同，如果凑不齐两条链，就空着作 0）。
2. 向上最长链。

分类

1. 如果无论如何都无法将时间全部用光，那么最简单，直接将向下最长链和向上最长链取较大值即可。
2. 否则的话……需要对路径进行拆分。

拆分和贪心

首先，很明显，下滑后不应该走回头路向上爬，这样做一定劣。

在上述情况 2 的基础上，我们进行贪心。

贪心原则：下滑后，仍然能滑动「时间限制」条不走回头路的边的前提下，尽可能向下滑到深度最小的节点。

滑到这样的节点后，计算下滑了的距离，再加上给定的时间限制，就是询问的答案。

注意：滑到这样的点之后，可能需要继续向下滑动。但是继续下滑的距离不用特意计算在答案内，因为已经被包含在答案里了。

至于如何贯彻这一贪心原则，我的办法是倍增，深度大的节点一定比深度小的节点更容易满足「能滑动时间限制条边」这一条件，因为深度大的节点还可以继续下滑到深度小的节点，但是深度小的节点不能走回头路。满足单调性。

太抽象了，举个例子：

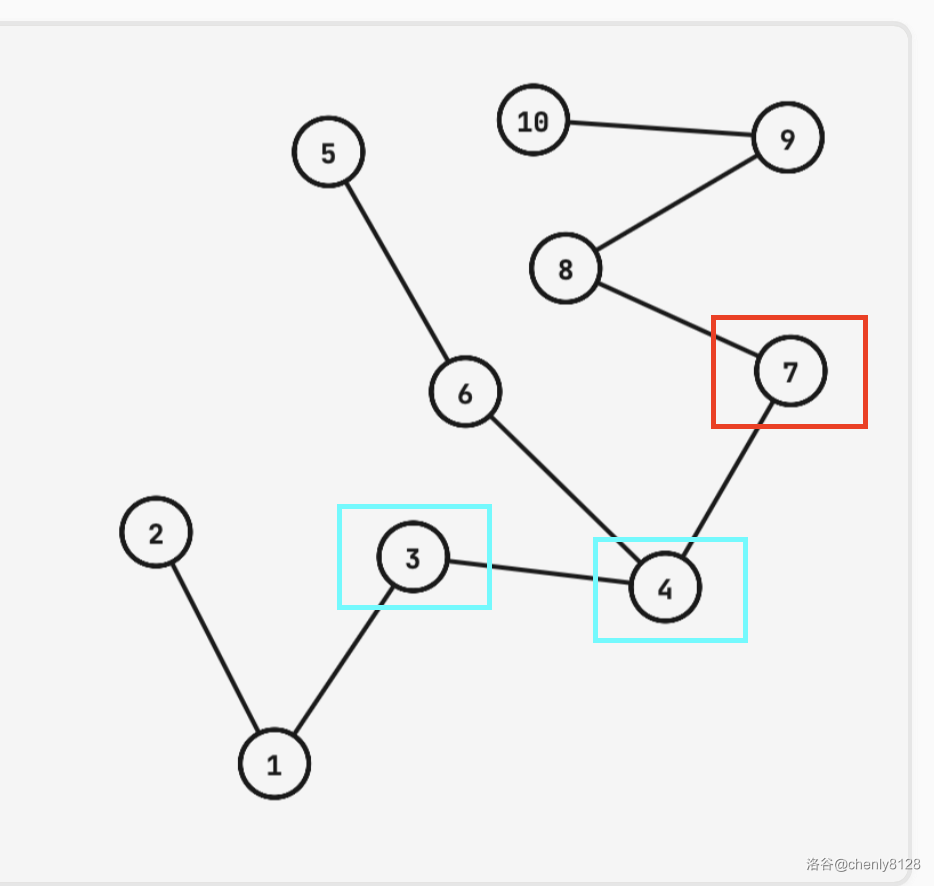
询问：从节点 7 出发，总共有 2 单位的时间。

通过倍增可以发现，下滑后，仍然能滑动时间限制条边的节点有：节点 7 自身、节点 4（从 4 到 2 的边数 为 3、从 4 到 5 也就是向下次长链长度为 2）和节点 3（从 3 到 2 的边数为 2）。但是由于节点 3 下滑得更多，所以贪心的选择节点 3。

所以答案为 $2+2 = 4$。第一个 $2$ 是下滑了距离；第二个 $2$ 是时间限制。实际路径为 7 -> 4 -> 3 -> 1 -> 2。

注意：在这里，虽然下滑到节点 3 之后，还在继续下滑，但是后面下滑的距离被包含在了「时间限制」部分，不用刻意计算。

代码

代码时间复杂度 $O((n + q) \log n)$，瓶颈在于倍增。

// Author: chenly8128
// Created: 2025-05-01 16:39:16

#include <bits/stdc++.h>
using namespace std;
inline int read(void) {
	int res = 0;bool flag = true;char c = getchar();
	while (c < '0' || c > '9') {flag ^= (c == '-');c = getchar();}
	while (c >= '0' && c <= '9') {res = (res << 3) + (res << 1) + (c ^ 48);c = getchar();}
	return flag ? res : -res;
}
const int MAXN = 2e5+10;
const int MLOG = 21;
int n,q,d,ans = 0,u,v;
int l1[MAXN],l2[MAXN],fr[MAXN],dp[MAXN],de[MAXN];
int step[MAXN][MLOG];
vector <int> g[MAXN];
int dfs1 (int x,int fa) {
	l1[x] = l2[x] = 0;
	step[x][0] = fa;
	for (int i = 1;i < MLOG;i++)
		if (step[x][i-1] == 0) break;
		else step[x][i] = step[step[x][i-1]][i-1];
	for (int y : g[x])
		if (y != fa) {
			de[y] = de[x]+1;
			int tmp = dfs1(y,x);
			if (l1[x] < tmp) {
				l2[x] = l1[x];
				l1[x] = tmp;
				fr[x] = y;
			}
			else if (l2[x] < tmp) l2[x] = tmp;
		}
	return l1[x]+1;
}
void dfs2 (int x,int fa,int k) {
	dp[x] = k;
	for (int y : g[x])
		if (y != fa)
			dfs2(y,x,max(k,(y == fr[x] ? l2[x] : l1[x])) + 1);
}
int main (void) {
	n = read(); q = read(); d = read();
	for (int i = 1;i < n;i++) {
		u = read(); v = read();
		g[u].push_back(v);
		g[v].push_back(u);
	}
	dfs1(1,0);
	dfs2(1,0,0);
	while (q--) {
		u = read(); v = read();
		if (d) {
			u ^= ans;
			v ^= ans;
		}
		int ori = de[u];
		if (max(dp[u],l1[u]) >= v) {
			for (int i = MLOG-1;i >= 0;i--) {
				if (step[u][i] > 0) {
					int t = step[step[u][i]][0];
					if (t == 0) continue;
					int p = max(dp[t],fr[t] == step[u][i] ? l2[t] : l1[t]);
					if (p >= v) u = step[u][i];
				}
			}
			int t = step[u][0];
			if (t != 0) {
				int p = max(dp[t],fr[t] == u ? l2[t] : l1[t]);
				if (p >= v) u = step[u][0];
			}
			printf ("%d\n",ans = v+ori-de[u]);
		}
		else printf ("%d\n",ans = max(dp[u],l1[u]));
	}
	return 0;
}