自动搬运

查看原文

来自洛谷，原作者为

	Siyuan Dream OIer.

搬运于2025-08-24 21:22:42，当前版本为作者最后更新于2018-12-03 23:20:42，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

$$\Large\texttt{My Blog}$$

题目链接：Luogu 1231

HansBug 眼前有 $n_1$ 本书，$n_2$ 本练习册，$n_3$ 本答案。已知一个完整的书册均应该包含且仅包含一本书、一本练习册、一本答案。现在 HansBug 只知道 $m_1$ 个可能的书和练习册的对应关系，$m_2$ 个可能的书和答案的对应关系。HansBug 想知道在这样的情况下，最多可能同时组合成多少个完整的书册。

数据范围：$n_1,n_2,n_3\le 10^4$，$m_1,m_2\le 2\times 10^4$

Solution

首先我们可以发现这就是一个网络流的模型。于是顺手把 $n_1+n_2+n_3$ 个点分成 $3$ 个部分，建立源点和汇点后跑最大流。写完才发现这样是有漏洞的，如下图所示：

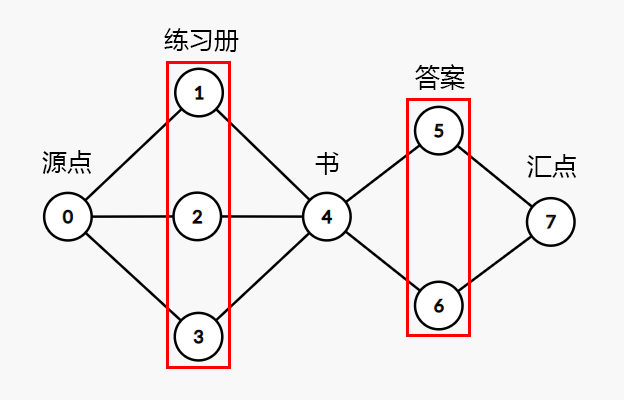
我们发现，如果按照上图跑最大流答案肯定是 $2$，而错误的原因就是书被重复使用了多次！所以我们还要保证每本书只能被使用一次！

因此我们就要引入拆点的思想。我们的目的是：即使一本书与多个联系册有关系，它流出的流量也只能是 $1$。所以我们把每个代表书的点拆成左右两个点，左边的点和练习册连边，右边的点和答案连边；当然左右对应点也要连一条容量为 $1$ 的边。那么我们可以得到下图：

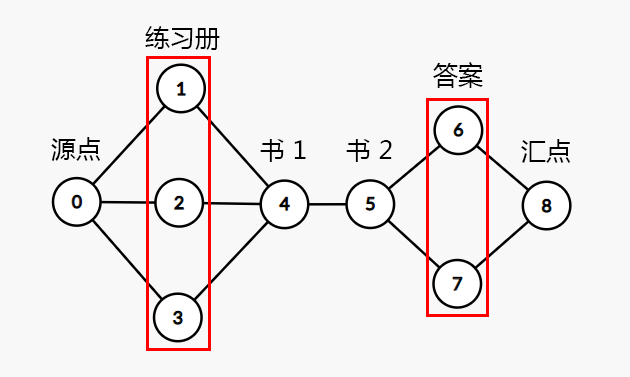
这样我们的答案就正确了，于是直接拆点后再跑最大流即可！

时间复杂度：$O(n^2m)$

Code

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>

const int N=4e4+5,M=1e6+5;
int n1,n2,n3,m,tot=1,lnk[N],ter[M],nxt[M],val[M],dep[N],cnr[N];

int id(int p,int x) {
	switch(p) {
		case 1: return x;
		case 2: return n2+x;
		case 3: return n2+n1+x;
		case 4: return n2+n1+n1+x;
	}
}
void add(int u,int v,int w) {
	ter[++tot]=v,nxt[tot]=lnk[u],lnk[u]=tot,val[tot]=w;
}
void addedge(int u,int v,int w) {
	add(u,v,w),add(v,u,0);
}
int bfs(int s,int t) {
	memset(dep,0,sizeof(dep));
	memcpy(cnr,lnk,sizeof(lnk));
	std::queue<int> q;
	q.push(s),dep[s]=1;
	while(!q.empty()) {
		int u=q.front(); q.pop();
		for(int i=lnk[u];i;i=nxt[i]) {
			int v=ter[i];
			if(!dep[v]&&val[i]) dep[v]=dep[u]+1,q.push(v);
		}
	}
	return dep[t];
}
int dfs(int u,int t,int flow) {
	if(u==t) return flow;
	int ans=0;
	for(int i=cnr[u];i&&ans<flow;i=nxt[i]) {
		cnr[u]=i;
		int v=ter[i];
		if(val[i]&&dep[v]==dep[u]+1) {
			int x=dfs(v,t,std::min(val[i],flow-ans));
			if(x) val[i]-=x,val[i^1]+=x,ans+=x;
		}
	}
	if(ans<flow) dep[u]=-1;
	return ans;
}
int dinic(int s,int t) {
	int ans=0;
	while(bfs(s,t)) {
		int x;
		while((x=dfs(s,t,1<<30))) ans+=x;
	}
	return ans;
}
int main() {
	scanf("%d%d%d",&n1,&n2,&n3);
	for(scanf("%d",&m);m--;) {
		int u,v;
		scanf("%d%d",&u,&v);
		addedge(id(1,v),id(2,u),1);
	}
	for(scanf("%d",&m);m--;) {
		int u,v;
		scanf("%d%d",&u,&v);
		addedge(id(3,u),id(4,v),1);
	}
	for(int i=1;i<=n1;++i) addedge(id(2,i),id(3,i),1);
	int S=0,T=n2+n1+n1+n3+1;
	for(int i=1;i<=n2;++i) addedge(S,id(1,i),1);
	for(int i=1;i<=n3;++i) addedge(id(4,i),T,1);
	printf("%d\n",dinic(S,T));
	return 0;
}