自动搬运

查看原文

来自洛谷，原作者为

	Zskioaert1106 值得一提的是，我在四个洛谷有 Remote Judge 的国外 OJ 上的账号都不是我的洛谷用户名。

搬运于2025-08-24 23:14:14，当前版本为作者最后更新于2025-06-11 18:04:34，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题目传送门：P12274 [蓝桥杯 2024 国 Python B] 设计

@123456wjc 说：“一想到二十年后如果 OI 还在，所有的小孩都必须人手掌握路径压缩和按秩合并，我就感到悲伤。”。

题目分析

题目要求查询连通性，所以考虑用并查集维护。

操作 1：合并 $x_i$ 和 $y_i$ 所属的集合。

操作 3：查询 $x_i$ 和 $y_i$ 是否在同一个集合内。

这两个可以轻松用并查集实现，不会的出门右转模板题。我们的重点在于操作 2，如何实现最近操作的撤销？

定义 $f_x$ 为 $x$ 所在集合的祖先，则合并前 $f_{f_x}=f_x$。发现（在朴素的并查集下），一次合并会使 $f_x \leftarrow y$，因此我们撤销时，只要让它变回自身就行了。

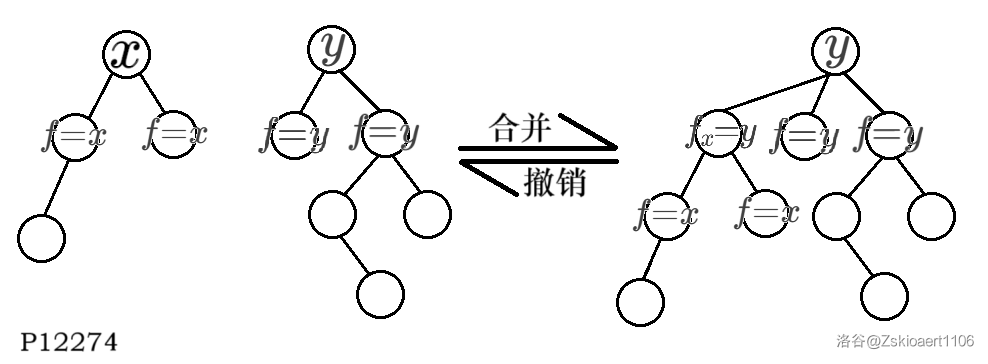
故使用栈维护：存储每次修改的 $f_x$ 位置，合并时入栈，遇到操作 2 就将栈顶的 $f$ 变回自身。特殊地，如果合并前 $x$ 和 $y$ 就在同一集合，则撤销对其没有影响，可以入栈一个特殊值（如 $0$）。

但是这样的并查集是无法路径压缩的，否则正确性就不保了。但朴素的并查集又会超时，于是考虑按秩合并。

按秩合并：对于并查集的两个树形集合 $x,y$，维护它们的深度，每次将深度小的合并到深度大的上。这样可以保证查询的最劣复杂度是 $O(\log n)$。

最终复杂度为 $O(n + m\log n)$。

代码实现

#include<iostream>
#include<stack>
using namespace std;
const int N=300005;
int n,m,f[N],dep[N];
int find(int x){
	if(f[x]==x)return x;
	return find(f[x]);
}
stack<int>t;
int main(){
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++)f[i]=i,dep[i]=1;
	while(m--){
		short op;
		int x,y;
		cin>>op;
		if(op==1){
			cin>>x>>y;
			x=find(x),y=find(y);
			if(x!=y){
				if(dep[x]>dep[y])swap(x,y);
				f[x]=y,dep[y]=max(dep[y],dep[x]+1);
				t.push(x);
			}
			else t.push(0);
		}
		else if(op==2){
			if(t.empty())continue;
			x=t.top();
			t.pop();
			if(x)f[x]=x;
		}
		else{
			cin>>x>>y;
			cout<<(find(x)==find(y)?"Yes":"No")<<'\n';
		}
	}
	return 0;
}

AC 记录。