自动搬运

查看原文

来自洛谷，原作者为

	Tomwsc 长风破浪会有时，直挂云帆济沧海

搬运于2025-08-24 23:13:51，当前版本为作者最后更新于2025-04-18 18:33:52，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

P12226 「WyOJ Round 1」启 · 破茧初阳 题解

思路

发现数据范围很大，所以我们考虑快速计算答案。如何快速计算答案呢？推式子！

很明显，这道题目只需要我们简单的推个式子即可。设在 $n$ 以内能被 $a$ 整除的数的个数为 $x$，能被 $\operatorname{lcm}(a,b)$ 整除的数的个数为 $y$，能被 $c$ 整除的数的个数为 $z$，能被 $\operatorname{lcm}(a,c)$ 整除的数的个数为 $p$，能被 $\operatorname{lcm}(a,b,c)$ 整除的数的个数为 $q$，答案为 $ans$，则有：

为什么，画个韦恩图然后容斥一下就清楚了……

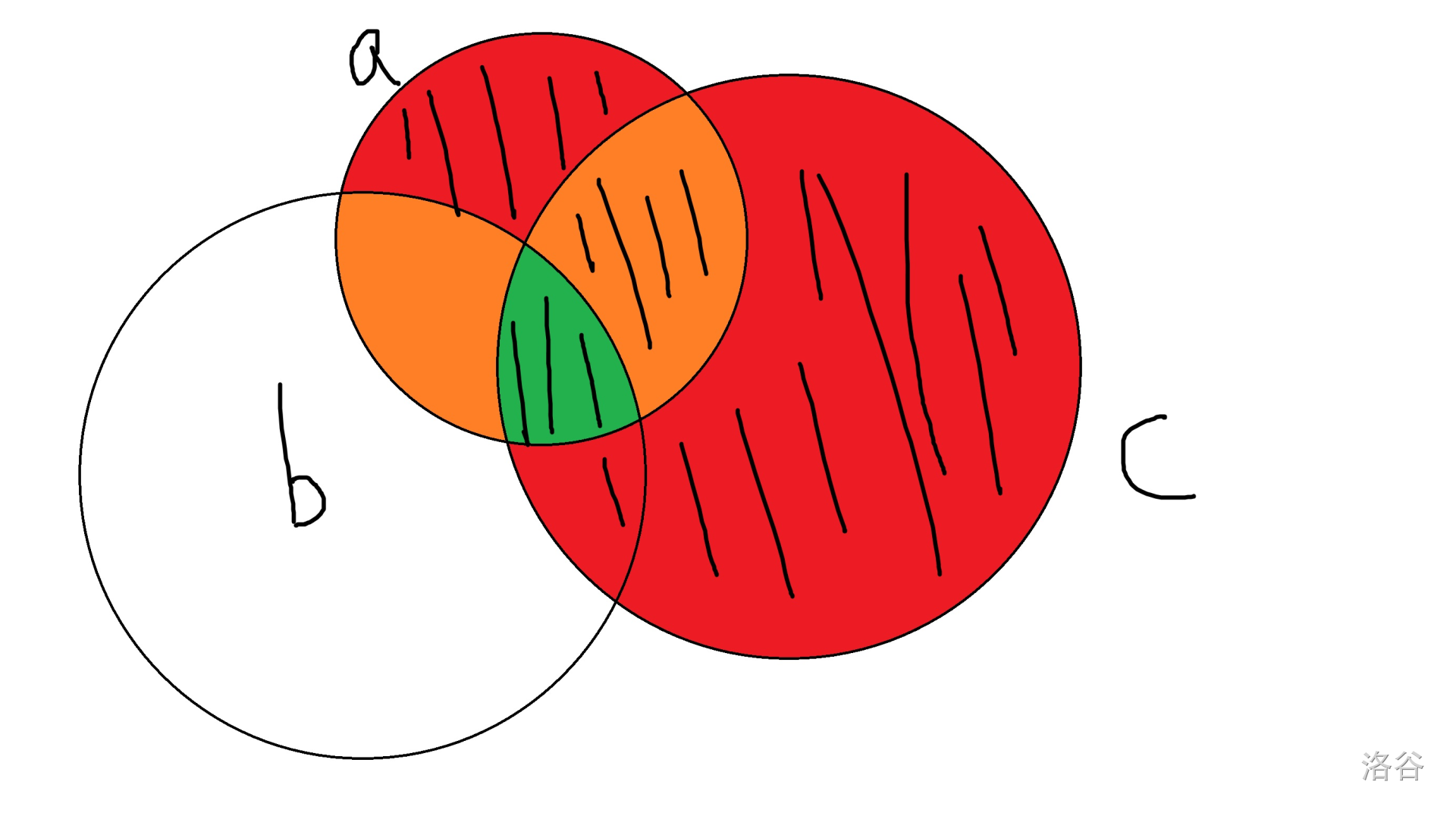
如图，阴影部分即为所求。所以令人想到用 $a$ 的圆圈加上 $c$ 的圆圈。但因为橙色部分会被多次计算，所以剪掉 $a$ 与 $b$ 以及 $a$ 与 $c$ 重合的部分，即 $\operatorname{lcm}(a,b)$ 和 $\operatorname{lcm}(a,c)$。此时，不难发现，绿色部分被多减掉了一次，所以还要再加回来，于是便有了加上绿色的部分，即 $\operatorname{lcm}(a,b,c)$。

接下来的问题就变成怎样计算最小公倍数了，有这么一个式子：

所以只要知道两数的最大公因数即可，辗转相除法可以计算两数的最大公因数，并且时间复杂度是 $O(\log \min(a,b))$。

代码

注意，数据很大，要开 __int128。

#include<bits/stdc++.h>
#define int __int128
#define inf (1ll << 62)
#define regint register int
#define pb push_back
#define mp make_pair
#define PII pair<int , int>
using namespace std;
int t , n , a , b , c;

int gcd(int a , int b) {
	if(!b)
		return a;
	return gcd(b , a % b);
}

inline int lcm(int a , int b) {
	return a / gcd(a , b) * b;
}

inline int read() {
	char c = getchar();
	int x = 0 , s = 1;
	while(c < '0' || c > '9') {
		if(c == '-')
			s = -1;
		c = getchar();
	}
	while(c >= '0' && c <= '9') {
		x = x * 10 + c - '0';
		c = getchar();
	}
	return x * s;
}

void write(int x) {
	if(x >= 10)
		write(x / 10);
	putchar(x % 10 + '0');
	return;
}

signed main() {
	t = read();
	while(t --) {
		n = read();
		a = read();
		b = read();
		c = read();
		write(n / a - n / lcm(a , b) + n / c - n / lcm(a , c) + n / lcm(lcm(a , b) , c));
		printf("\n");
	}
	return 0;
}