自动搬运

查看原文

来自洛谷，原作者为

	Clclclcl **

搬运于2025-08-24 23:13:06，当前版本为作者最后更新于2025-04-22 19:06:47，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

这题和这 Island 这题类似，是基环树直径的板子，不过这题是边权改成点权罢了，因为题目规定是每条边只能经过一次，没有规定点只能走一次且权值在点上，所以存在一种特殊情况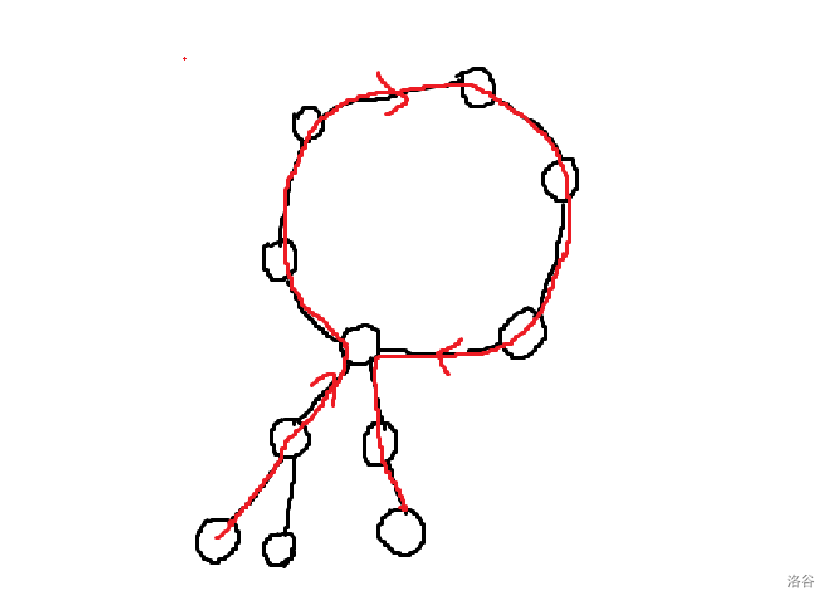： 这种可以从环上一个子树内出发绕过环回到该子树，这明显不是基环树的直径，即环上权值和+某棵子树的根节点最长路径+该棵子树根节点的次长路径。特判完这种情况剩下的就是基环树直径板子了。

接下来考虑基环树直径怎么求？首先基环树最经典的思路是把环上每个点当成一棵子树的根，将基环树拆成若干子树再进行分析。 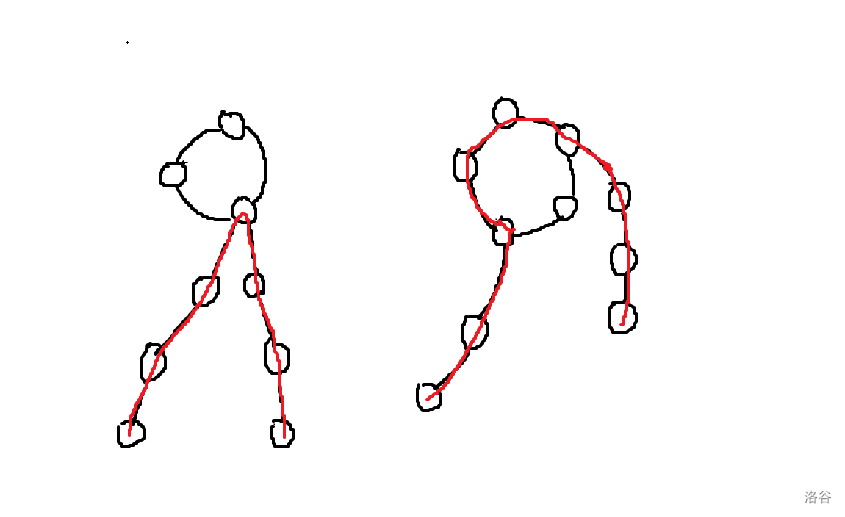如上图，基环树直径分俩种情况，一种是挂在某一棵子树上，一种是经过某一棵子树的最长链再经过环走到另一棵子树的最长链。

对于第一种情况就是求树的直径的经典求法，不会的同学可以做树的直径这题。不过我们需要先找到基环树的环对环上每个点当根求树的直径，预处理出每个节点当根的最长链（这我们后面考虑第二种情况需要用到），对于找环拓扑排序即可很容易求得。

第二种情况就稍微麻烦，需要用到单调队列优化环上 DP。设 $f[i]$ 为以 $i$ 为根的最长链，设环上 $i$,$j$ 俩点的距离为 $dist$,$w[i]$ 为点权，那么俩棵子树最大距离为 $f[i] - w[i] + dist + f[j] - w[j]$。

环上问题最经典的操作是破环成链，将环拆开复制一遍接到后面，设 $dist[i]$ 为 $[1,i]$ 的路径点权前缀和，$f[i]$ 为减去 $i$ 点点权的最长链，减去点权因为会和 $dist$ 数组重复计算该值。 那么式子应该为：$dist[i] - dist[j - 1] + f[i] + f[j]$ 可以发现要使得该值最大需要 $(f[j] - dist[j - 1])$ 最大，设环长为 $cnt$ ,则应该取区间 $[\max(1,i - cnt + 1),i - 1]$ 的最大值，很明显可以使用单调队列优化这一过程，单调队列维护 $f[i] - dist[i - 1]$ 的最大值转移即可。下面是具体代码细节。

# include <bits/stdc++.h>

using namespace std;
# define pb push_back
# define fi first
# define se second
typedef pair<int,int> PII;
int n, m,k;

void solve() {
    cin >> n;
    vector <vector<int>> g(n + 1);
    vector<int> d(n + 1,0),w(n + 1,0);
    for(int i = 1;i <= n;i ++ ) cin >> w[i];
    for(int i = 1;i <= n;i ++ ){
    	int l,r;
    	cin >> l >> r;
    	g[r].pb(l);
    	g[l].pb(r);
    	d[r] ++;
    	d[l] ++;
    }
    vector<int> st(n + 1,0);
    vector<int> f1(2 * n + 2,0),f2(2 * n + 1,0); // f1 为子树内最长链,f2 为次长。
    vector<int> vis(n + 1,0);
    auto work = [&] (int root) ->int{
    	int ans = 0;
    	queue <int> q1; 
    	for(int i = 1;i <= n;i ++){
    		st[i] = 1;
    		if(d[i] == 1){
    			q1.push(i);
    		}
    	}
    	while(q1.size()){
    		auto u = q1.front();
    		q1.pop();
    		vis[u] = 1;// topsort 标记环。
    		for(auto l : g[u]){
    			if( -- d[l] == 1) q1.push(l);
    		}
    	}

    	auto dfs = [&] (auto dfs,int u,int fa) -> void{
            f1[u] = w[u],f2[u] = w[u];
    		for(auto l : g[u]){
    			if(!vis[l] || l == fa) continue;
    			dfs(dfs,l,u);
    			if(f1[l] + w[u] > f1[u]){
    				f2[u] = f1[u];
    				f1[u] = f1[l] + w[u];
    			}
    			else f2[u] = max(f2[u],f1[l] + w[u]);
    		}
    		ans = max(ans,f1[u] + f2[u] - w[u]); //这是第一种情况。
    	};
    	int st = 0,cnt = 0;
    	for(int u = 1;u <= n;u ++ ){
    		if(!vis[u]){ // 拆环,对于环上每个点当 root 跑树的直径。
    			st = u;
    			++ cnt; // 累计环长。
    			dfs(dfs,u,0);
    		}
    	}
        // 对于环上点重新赋值下标方便破环成链。
    	vector<int> dp(2 * cnt + 2,0),dist(2 * cnt + 2,0),dp1(2 * cnt + 1,0);
    	int id = 0;
    	int pre = 0;
    	auto dfs1 = [&] (auto dfs1,int u,int fa) ->void{
    		dp[++ id] = f1[u] - w[u]; // 环上每个点重新赋 id,减去点权因为会和 dist 数组重复计算。
            dp1[id] = f2[u] - w[u];
            dist[id] = w[u];
    		vis[u] = 1;
    		for(auto l : g[u]){
    			if(l == fa || vis[l]) continue;
    			dfs1(dfs1,l,u);
    		}
    	};
    	dfs1(dfs1,st,0);

        // 破环成链，复制一遍。
    	for(int i = 1;i <= cnt;i ++ ) dp[i + cnt] = dp[i],dist[i + cnt] = dist[i];
    	for(int i = 1;i <= 2 * cnt;i ++ ) dist[i] += dist[i - 1];//环上前缀和。
        // 这是这一题的坑点,需要特判环上点权之和加上某一棵子树根的最长链加次长链。
        for(int i = 1;i <= cnt;i ++ ) ans = max(ans,dist[cnt] + dp[i] + dp1[i]);
        deque <PII> q;
    	for(int i = 1;i <= 2 * cnt;i ++ ){
    		while(q.size() && i - q.front().fi + 1 > cnt) q.pop_front(); // 保证区间不超过环长
    		if(q.size()){
    			ans = max(ans,dp[i] + q.front().se + dist[i]);
    		}
    		while(q.size() && q.back().se < dp[i] - dist[i - 1]) q.pop_back(); // 维护队列单调。
    		q.pb({i,dp[i] - dist[i - 1]});
    	}

    	return ans;
    };
    
    int res = 0;
    for(int i = 1;i <= n;i ++ ){ // 该题不是基环树森林可不必枚举每个点。
    	if(!st[i]){
    		st[i] = 1;
    		res += work(i);
    	}
    }
    cout << res << endl;
}
signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int _ = 1;
    //cin >> _ ;
    while( _ -- )
    {
        solve();
    }
    return 0;
}