自动搬运

查看原文

来自洛谷，原作者为

	Souture **

搬运于2025-08-24 23:13:06，当前版本为作者最后更新于2025-04-13 18:56:04，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

题目大意

在二维平面上有 $$n$$ 个地雷，地雷的覆盖范围可以看成一个圆，第 $$i$$ 个地雷的位置为 $$(x_i, y_i)$$，半径为 $$r_i$$，你要从原点 $$(0, 0)$$ 走直线出发，方向限制在 $$\left[0, \frac{\pi}{2}\right]$$ （第一象限），求你走的直线与任何一个圆不交的概率。

如图：

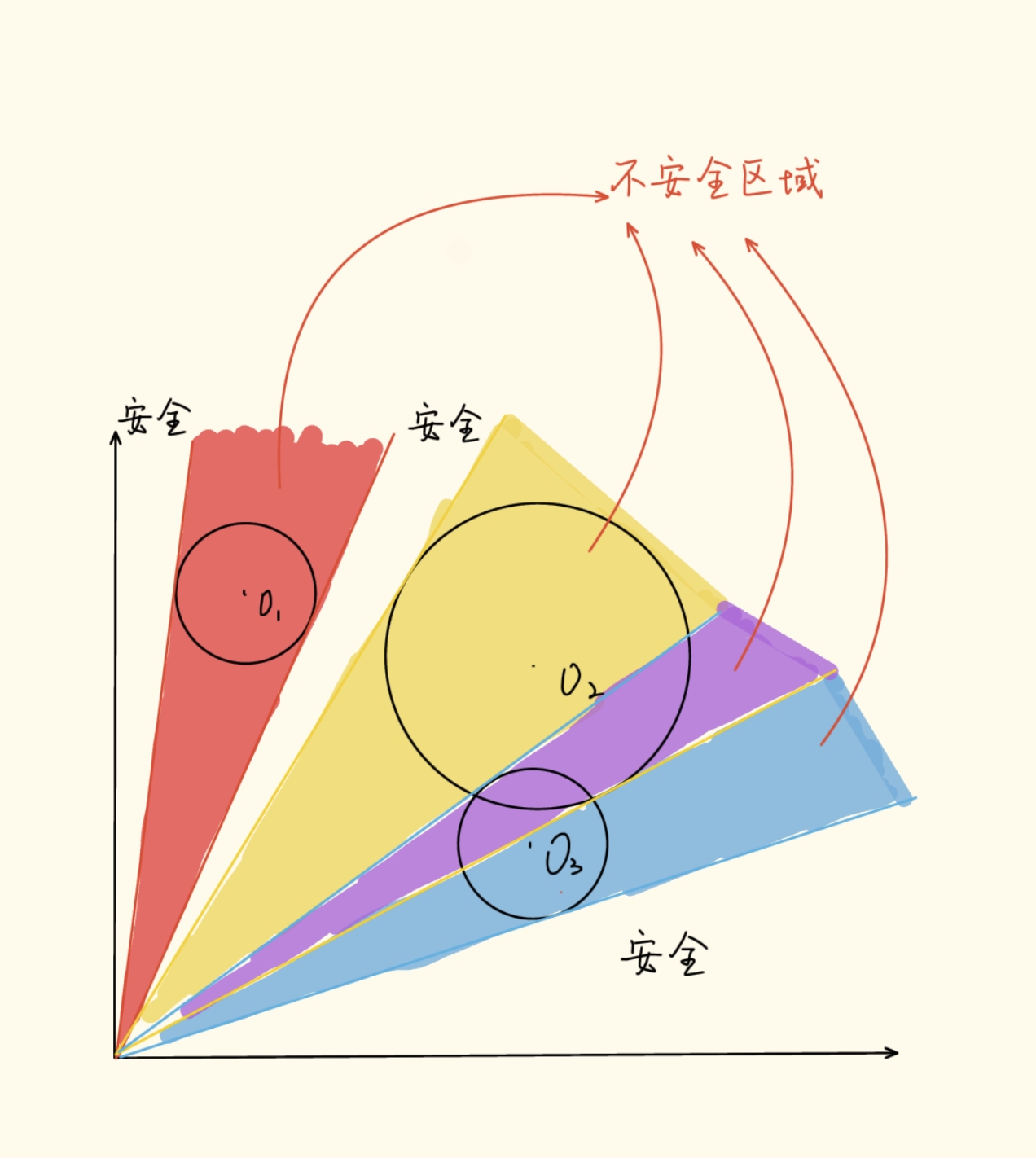
思路

由于是要求概率，我们设与平面上所有圆不交的角度之和为 $$\theta$$ 不难想到答案是：

$$\frac{\theta}{\frac{\pi}{2}}$$

直接求与圆不交的角度和很困难，考虑单个圆单独处理，先求直线与每个圆相交的角度和 $$ \alpha$$ ，最后用 $$\frac{\pi}{2} - \alpha $$ 表示 $$ \theta $$。

转换为角度区间

对于每个地雷，先计算其与原点连线的方向角

$$\theta = \arctan\frac{y}{x}$$

如图：

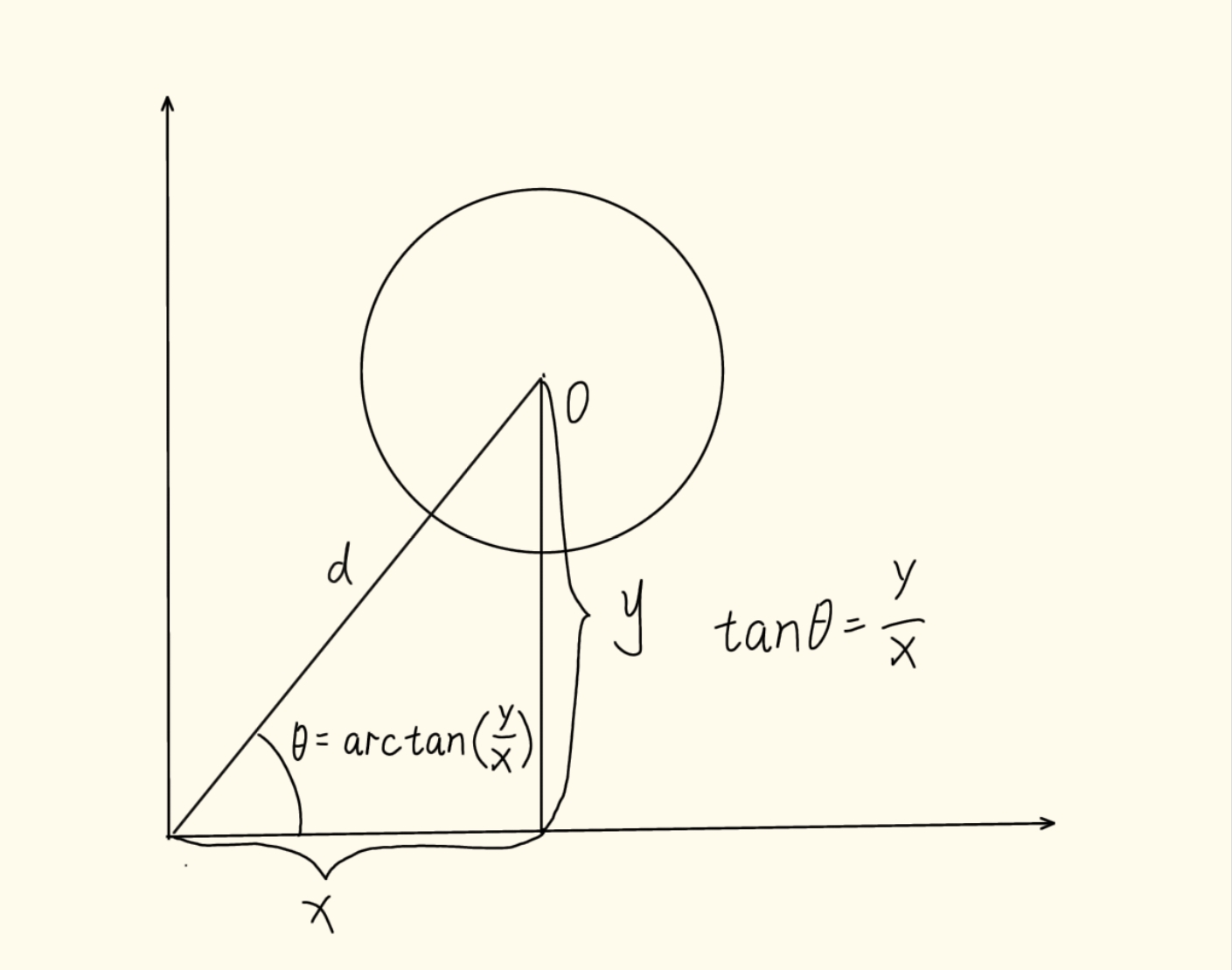
以及原点到地雷的距离

$$d = \sqrt{x^2+y^2}.$$

地雷影响的方向范围为

$$[\theta-\delta,\ \theta+\delta]$$

其中

$$\delta = \arcsin\left(\frac{r}{d}\right).$$

如图：

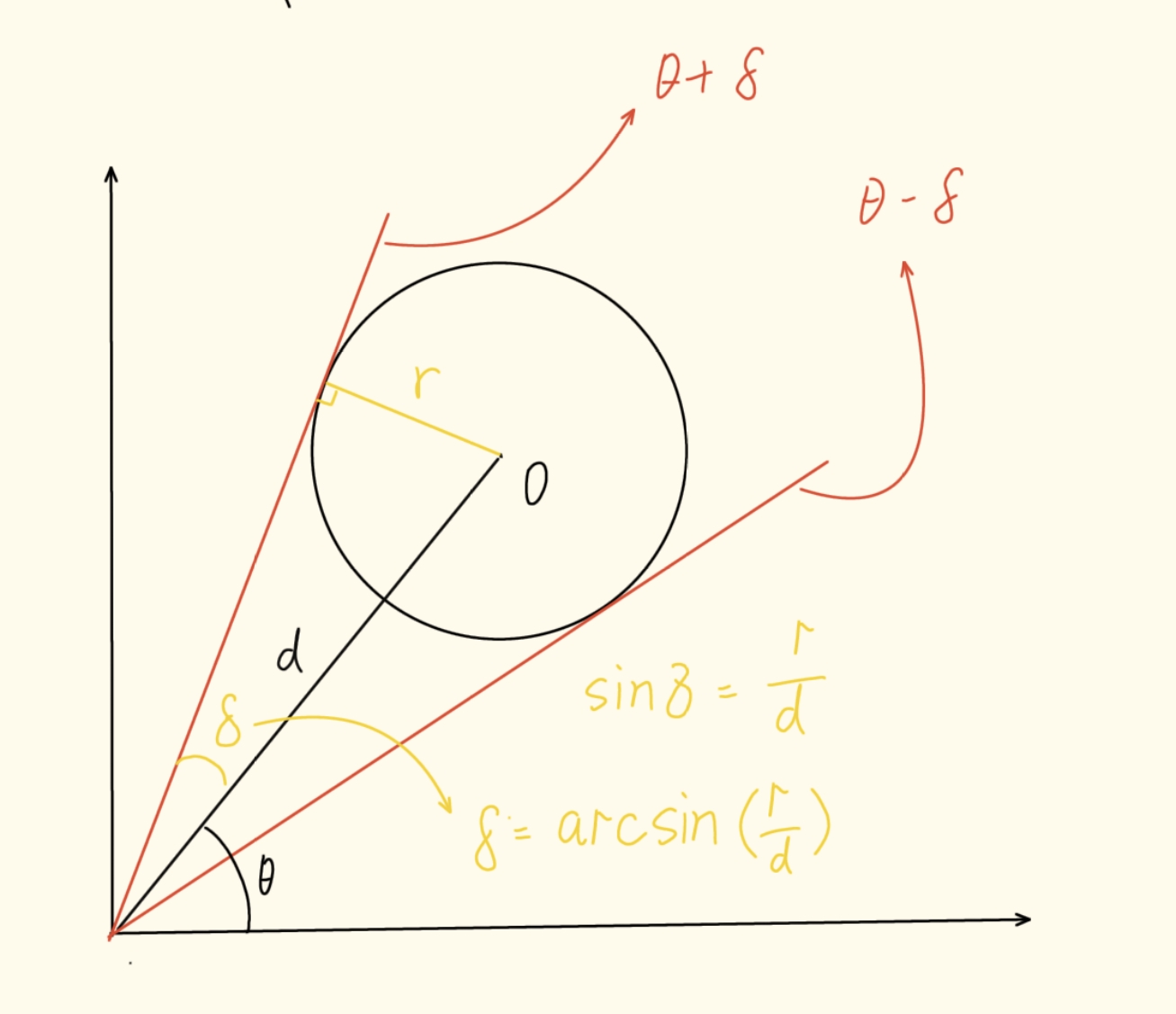
由于题目保证了 $$r_i < \min{(x_i, y_i)}$$，所以不需要对边界进行处理，即

$$\left[\theta-\delta,\ \theta+\delta\right] \subset \left[0, \frac{\pi}{2}\right] $$

扫描线

显然我们对每个圆的区间计算后位置很乱，考虑将所有地雷对应的角度区间排序后，利用扫描线合并所有重叠的区间，从而得出不安全角度 $$ \alpha $$ 的总长度。

我们记扫描线为 $$line$$ ：

假设已经按区间的左端点 $$L$$ 从小到大排序。那么，对于每个区间 $$[L, R]$$：

每次定位扫描线

$$line = \max(line, L)$$

如果当前区间的左端点 $$L$$ 在 $$line$$ 之前，说明新区间与之前的合并区间已有重叠，此时将 $$line$$ 保持在合并区间的右边界。

如果 $$L$$ 大于 $$line$$，表示上一个合并区间结束，扫描线移动到新区间起始点开始计算新的覆盖部分。

累加新覆盖的部分

$$\alpha += \max(0.0, R - line)$$

这一步计算当前区间 [$$L, R$$] 对比扫描线位置 $$line$$ 之后，新扩展出来的部分。如果 $$R > line$$，则 $$R - line$$ 就是当前区间新增的长度；否则没有新增部分。

更新扫描线位置

$$line = \max(line, R)$$

确保扫描线总是记录已合并区间最新的右边界，便于后续区间计算合并长度。

如图：

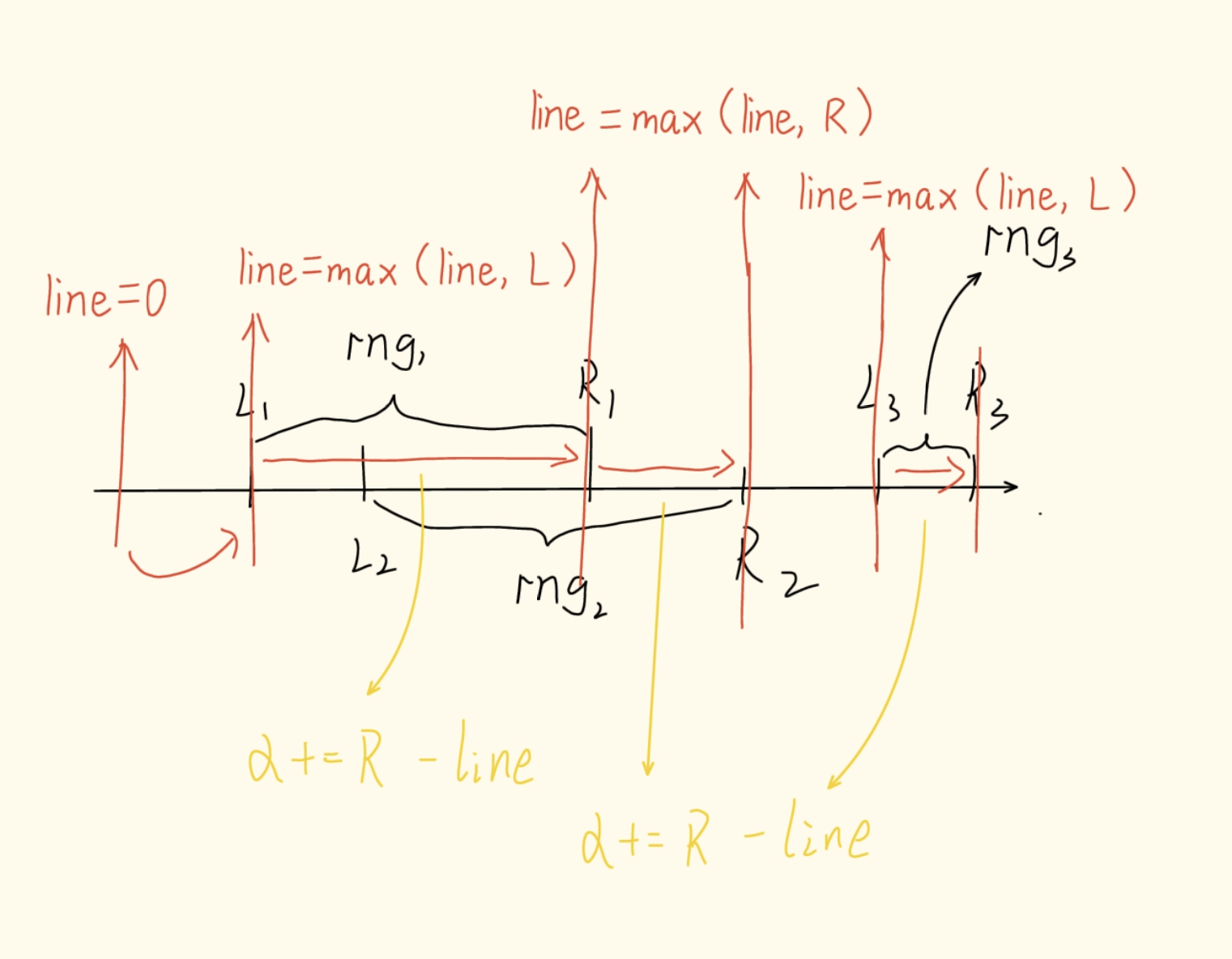
计算结果

安全角度的角度和 $$\theta$$ 为

$$\theta = \frac{\pi}{2} - \alpha$$

最终通关概率为

$$\text{ans} = \frac{\theta}{\frac{\pi}{2}} = \frac{\frac{\pi}{2} - \alpha}{\frac{\pi}{2}} $$

小技巧

基于C++的库函数，我们可以使用

$$\pi = acos(-1)$$

来获得高精度的常量 $$\pi$$ 。

代码

#include <bits/stdc++.h>
using namespace std;

#define endl '\n'
#define all(v) v.begin(), v.end()

const double PI = acos(-1);

void sol()
{
    int n; cin >> n;
    vector<tuple<int,int,int>> p(n);
    for (int i = 0; i < n; i++) {
        int x, y, r;
        cin >> x >> y >> r;
        p[i] = {x, y, r};
    }
    
    vector<pair<double,double>> rng;
    for (auto &[x, y, r] : p) {
        double t = atan2(y, x);
        double d = sqrt(x * x + y * y);
        double det = asin(r / d);

        double L = t - det, R = t + det;
        rng.push_back({L, R});
    }
    
    sort(all(rng), [&](auto a, auto b) { 
        return a.first < b.first; 
    });

    // 扫描线
    double line = 0;
    double res = 0;
    for (auto &[L, R] : rng) {
        line = max(line, L);
        res += max(0.0, R - line);
        line = max(line, R);
    }
    
    double ans = (PI / 2 - res) / (PI / 2);
    cout << fixed << setprecision(3) << ans << endl;
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    sol();
    return 0;
}