自动搬运

查看原文

来自洛谷，原作者为

	brofea5 人生就像动态规划，在早已给定的值里反反复复地找最优解

搬运于2025-08-24 23:12:58，当前版本为作者最后更新于2025-04-12 18:45:28，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

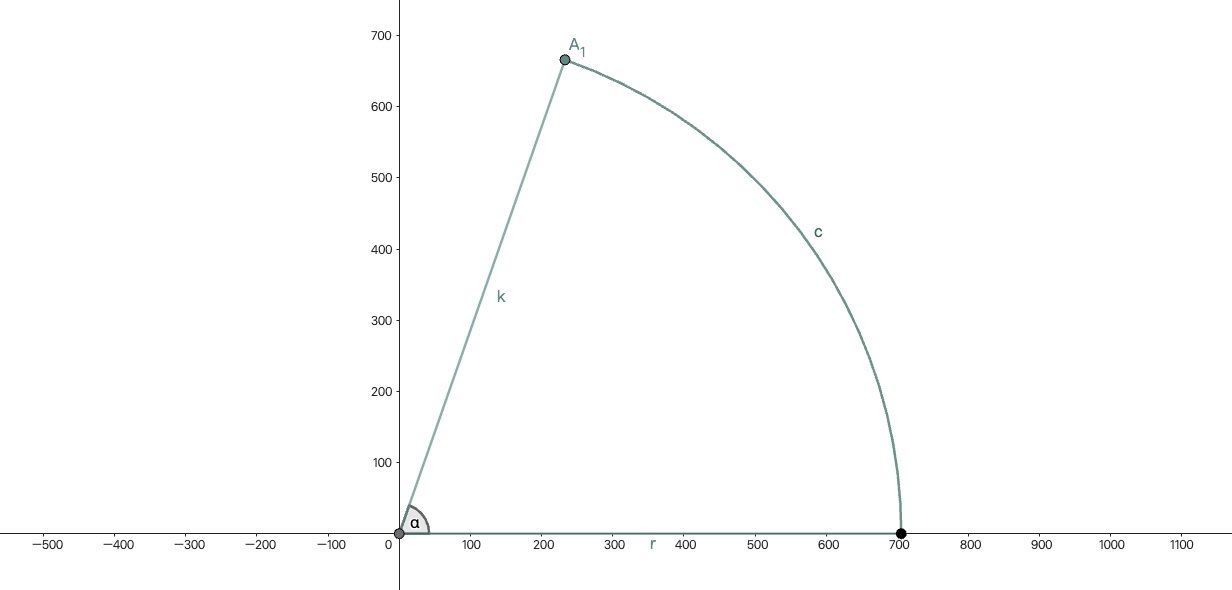
题意

一个点有两种移动方式，沿着 $x$ 轴正方向移动、以原点为圆心旋转，问走到点 $(233,666)$ 需要经过的路程

答案四舍五入至整数

思路

答案很简单，计算原点到 $(233,666)$ 的距离 $r=\sqrt{233^2+666^2}$，沿着 $+x$ 移动 $r$，再旋转至终点

旋转的角度 $\theta=\arcsin(666/r)$

最终的路程就是：（四舍五入至整数）

$$S=r+\frac\alpha{2\pi}\cdot 2\pi r=r(1+\arcsin(666/r))\approx 1576 $$

如果忘记 C++ 有 asin() 函数（$\arcsin$ 函数）了怎么办呢？

• 用 sin() 函数数值逼近，可以从 0.0000001 循环到 3.1400000，也可以用二分
• 在终端里用 python 的 math.asin() 函数
• 用 Excel 的 ASIN() 函数，如果不记得函数名可以在“告诉我”中搜索“函数”并寻找反函数
• 泰勒展开

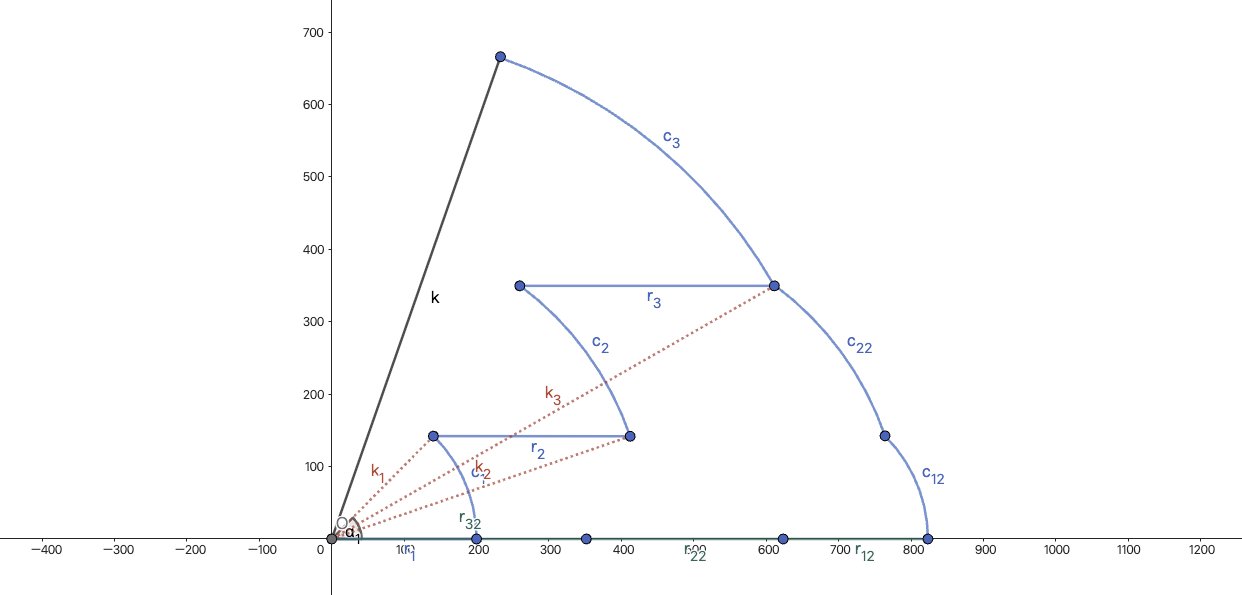
要证明这个走法就是最佳的其实还挺麻烦，不过在几何上就比较好理解，假设有这么一条路径 $r_1,c_1,r_2,c_2,r_3,c_3$

把所有圆弧平移到右侧首尾相连，把所有线段平移到 $x$ 轴上，可以看出线段一定长于原本的 $r$，圆弧和一定长于原本的 $c$ （可以用三角不等式证明）

严谨来说，应该用微积分证明，我们将每一次移动都看作是微小的坐标变化$(\delta x_i,\delta y_i)$

对于点 $(x,y)$ ，旋转微小角 $d\theta$ 的距离变化为 $r=x^2+y^2$，旋转，则路程为 $\delta L_R=r\,d\theta$，对于沿 $x$ 轴平移，路程为 $\delta L_T=\delta x$，此时 $\theta=\arctan(y/x)$，随着 $x$ 增大而增大

$d\theta$ 极小时，约束条件可为：

$$\sum_{i\in T} \delta x_i +\sum_{j\in R} (-y_j\,d\theta_j) \;=\;233 ,\sum_{j\in R} x_j\,d\theta_j\;=\;666 $$

综上可以构造拉格朗日函数：

$$\mathcal{L}=\sum_{i\in T} \delta x_i+\sum_{j\in R} r_j\,d\theta_j +\lambda\Biggl( \sum_{i\in T} \delta x_i +\sum_{j\in R} (-y_j\,d\theta_j)-233\Biggr) +\mu\Biggl(\sum_{j\in R} x_j\,d\theta_j-666\Biggr)\,, $$

对 $\delta x_i$ 求偏导数，可以求出 $\lambda=-1$，然后考虑旋转的部分，可以设

$$f_j = r_j\,d\theta_j -\lambda\,y_j\,d\theta_j+\mu\,x_j\,d\theta_j=d\theta_j\Bigl(r_j + y_j+\mu\,x_j\Bigr)\,. $$

求偏导后可知，每个旋转操作要满足：

$$\frac{\partial f_j}{\partial (d\theta_j)}=r_j + y_j+\mu\,x_j=0\tag1 $$

注意到每次旋转都是绕原点进行，$x_j,y_j$ 由之前的运动决定，而又要使得在每个旋转的贡献中使得 $\mu$ 保持一致，则各个旋转都必须满足上式

考虑理想的候选方案，设目标点为 $(r_f,\theta_f)$ 若先水平平移至 $(r_f,0)$，则对于所有在这点的旋转操作都有

$$r_j + y_j+\mu\,x_j=r_f+0-1\times r_f=0$$

正好满足（1）且每个旋转必要条件一致

若在平移未完成前旋转，即 $x<r_f$ 或 $y\ne0$。将（1）写为：

$$\sqrt{x_j^2+y_j^2}+y_j+\mu\,x_j=0$$

若在平移还未完成时就引入旋转，那么（1）要求的 $\mu$ 会因不同步而不可能一致地取一个常数，而会取一个更“严格”的值，使得后续整体代价增大，也就是说无法找到一个 $\mu$ 满足所有旋转步都不发生效率损失

在这道题中，$\mu$ 恒定事实上使得 $\theta$ 为一个差为 $0$ 的等差旋转角，也就是说，每次都旋转 $\theta_j$ 走到终点的路径就是最短的，对于任何终点都成立，这点在几何上不难证明

走多少次都是一样的，那就走一次吧

AC 代码：

#include <bits/stdc++.h>
int main() {
  double r = sqrt(233 * 233 + 666 * 666);
  int res = r + asin(666.0 / r) * r;
  std::cout << res;
}