自动搬运

查看原文

来自洛谷，原作者为

	WYXkk Zzz Zzz

搬运于2025-08-24 23:12:29，当前版本为作者最后更新于2025-04-07 14:03:18，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

为了炫耀我拿下了本题赛时一血，我决定跑来写个题解。

题目描述看似很复杂，实际上也确实有点复杂。但是如果你玩过《14种扫雷变体2》，你会在看到题目后立刻意识到这就是 [2T] 无三连 + [2B] 桥，虽然这对解题并没有太大帮助。实际上出题人就是玩家群群友，此前还在致理杯 div2 上放了一个 [1S] 蛇 + [2B] 桥。

样例解释提供了一个直观理解后两个条件的方式：黑格形成从左侧到右侧的 $k$ 座桥，每座桥的相邻两个雷水平或斜向相邻。同时，通过观察样例（其实不看也不是很难想到），可以发现下面两个结构：

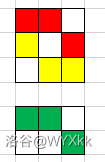
这两个结构的密铺都满足条件（纵向必须在整数份处截断）且可以拼接，这样就能对很多组 $(n,k)$ 构造出一个解。比如一个 $n=10,k=6$ 的解长这样：

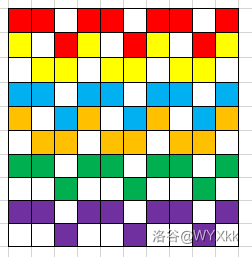
如果一个这样的解使用了 $a$ 份第一个结构和 $b$ 份第二个结构，那么 $n=3a+2b,k=2a+b$，即 $a=2k-n,b=2n-3k$。于是，如果 $2k-n\ge 0$ 且 $2n-3k\ge0$，那么上面的结构的组合就可以给出一个解。大胆猜测其他情况都无解即可通过本题。 代码较为简单，这里略去。但是由于这是一份题解，这里不得不给出证明。

每列的 $n$ 格中都有 $k$ 格染黑。在无三连的限制下，每三格最多只能染黑两格。

• 如果 $n=3a$，那么自然 $k\le 2a$。

• 如果 $n=3a+1$，那么 $k\le 2a+1$，且 $k=2a+1$ 时，每一列的最后一格都必须染黑，在 $n\ge3$ 时就会出现横向黑色三连，所以 $k\le 2a$。

• 如果 $n=3a+2$，那么 $k\le 2a+2$，且 $k=2a+2$ 时，每一列的最后一格都必须染黑，在 $n\ge3$ 时就会出现横向黑色三连，所以 $k\le 2a+1$。

综上所述，有解时必然 $2n-3k\ge0$。

第一座桥不会经过 $(3\sim n,2\sim n-1)$。否则如果它经过了其中的 $(a,b)$，由于纵向一次只能上下一格，它就无法经过 $(1,b-1\sim b+1)$，从而出现了白色三连。这在玩家群里有个名字，叫“光锥定式”。如果你通过一些正确的相对论科普知道了光锥的含义，你应该会觉得这相当形象。

再用一次光锥定式，可以得到第二座桥不会经过 $(5\sim n,3\sim n-2)$，否则第三行会出现白色三连。同理，第三座桥不会经过 $(7\sim n,4\sim n-3)$。以此类推，第 $k-1$ 座桥不会经过 $(2k-1\sim n,k\sim n+1-k)$。

再反过来考虑最后一座桥，它不会经过 $(1\sim n-2,2\sim n-1)$，否则最后一行会出现白色三连。在 $k\ge 2$ 时，如果 $n>2k$，即 $n\ge 2k+1$，则 $(n-2,k\sim k+2)$ 既无法被前 $k-1$ 座桥覆盖也无法被被最后一座桥覆盖，从而出现了白色三连。在 $k=1$ 时，由于 $n\ge 4$，这座桥无法经过 $(1\sim n,2)$，矛盾。所以，有解时必然 $2k-n\ge0$。

本题并未涉及 $n\le 3$。上面的两个结论都部分依赖 $n\ge4$，所以在更小的时候是有反例的。具体而言，$(n,k)=(3,1),(2,2),(2,0),(1,1),(1,0)$ 并不满足上面两个条件，但是有解。构造非常简单，略。

这就是玩《14种扫雷变体》和《14种扫雷变体2》给我带来的自信.jpg