自动搬运

查看原文

来自洛谷，原作者为

	xxy_free_ioi ​博观而约取，厚积而薄发 | 最后在线时间: 2025/8/22 17:05

搬运于2025-08-24 23:12:08，当前版本为作者最后更新于2025-04-04 23:09:01，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

P12015 [NOISG 2025 Finals] 怪物

毒瘤

解法

易得，此题为贪心。

我们来想想贪心的策略，首先，我们很显然的可以想到一个解法：在有怪物地雷肯定是要引爆的。计算每一只怪物移动到附近地雷的代价（加上引爆代价），如果它小于等于这只怪物的生命值 $h_i$，那么我们就选择移动并引爆，否则直接敲死即可。但是，这样明显是错误的，我们不应该将怪物移动到地雷上就引爆，应该看看有没有其他怪物也要移动到这里，一起引爆，能省更多的钱，那么我们就需要定义一个数组 $st$ 来表示这里是否已经有怪物了。至于为啥是小于等于 $h_i$ 呢，原因是你占一个地雷说不定可以让其他怪物更少花费便可以被杀死。而判断移动到附近地雷的代价，我们只要将 $x$ 数组排序，使用 lower_bound 即可。

这样，我们的代码就初具雏形了，欸，交上去怎么只要 14 pts？仔细想想，发现是想漏了一种情况，比如说：

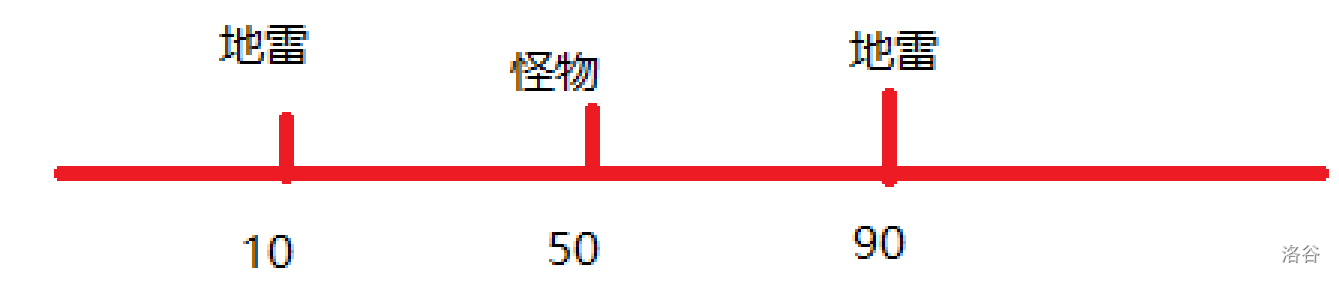
这种怪物处于中间（并且两边移动花费（包括引爆费用）相同，移动花费小于怪物生命值）的情况又怎么办呢？哦，我们应该将怪物的位置也进行排序，这样，前面的已经全部处理完了，我们只需要考虑后面的，自然是向后移动啦！

代码

理清了思路，代码就很好写了。

#include <bits/stdc++.h>

using namespace std;

#define int long long

const int N = 2e5 + 10;

struct Monster {
    int a, h;
    bool operator< (const Monster& W) {return a < W.a;}
} monsters[N];

int n, k, res;
int x[N], st[N];

signed main() {
    ios::sync_with_stdio(0);
    cin.tie(0);

    cin >> n >> k;
    for (int i = 1; i <= n; i++) cin >> monsters[i].a >> monsters[i].h;
    for (int i = 1; i <= k; i++) cin >> x[i];

    sort(x + 1, x + k + 1);
    sort(monsters + 1, monsters + n + 1);
    
    for (int i = 1; i <= n; i++) {
        int a = monsters[i].a;
        int p = lower_bound(x + 1, x + k + 1, a) - x;
        if (a == x[p]) st[p] = 1;
    }
    for (int i = 1; i <= n; i++) {
        int a = monsters[i].a, h = monsters[i].h;
        int p = lower_bound(x + 1, x + k + 1, a) - x;
        int c1 = a - x[p - 1], c2 = x[p] - a,
            t1 = !st[p - 1], t2 = !st[p];
        if (p == 1) {
            if (c2 + t2 <= h) st[p] = 1;
            res += min(h, c2);
        } else if (p == k + 1) {
            if (c1 + t1 <= h) st[p - 1] = 1;
            res += min(h, c1);
        } else if (c1 + t1 < c2 + t2) {
            if (c1 + t1 <= h) st[p - 1] = 1;
            res += min(h, c1);
        }  else {
            if (c2 + t2 <= h) st[p] = 1;
            res += min(h, c2);
        }
    }

    for (int i = 1; i <= k; i++) 
        res += st[i];
    
    cout << res << '\n';

    return 0;
}