自动搬运

查看原文

来自洛谷，原作者为

	Scinerely 可恶

搬运于2025-08-24 23:11:54，当前版本为作者最后更新于2025-06-22 19:00:49，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

这个题目有说法的。

我们考虑 ? 的连续段只有两种本质不同的情况，它们分别是：

• A...A 。如果我们往里面全部填入 A 肯定是最好的，产生 $+0$ 的代价；如果往里面填入 AB 或者 AC ，产生 $+2$ 的代价；如果三种字母全部填入，即 ABC ，产生 $+3$ 的代价。

• A...B 。填入 AB 已经是最优情况，但是也有 $+1$ 的代价；填入 ABC 会产生 $+2$ 的代价。

为了避免误会，这里所说的加入 AB，AC，ABC 是指允许在这一段 ? 中填入这些字符的含义，不需要每一种字符都出现。

我们现在看看，假设我们给每一个 ? 的连续段都确定了类型（A，B，C，AB，AB，BC，ABC 之一），对于某一个询问 $(X,Y,Z)$ 是否存在一个可行的方案呢？

给出的结论是，记录 $cnt_{A,1}$ 表示仅仅允许填入 A 的连续段长度之和；$cnt_{A,2}$ 表示可以填入 A 的连续段长度之和。其余两种字母同理。如果 $cnt_{A,1} \leq X \leq cnt_{A,2}$ ，$cnt_{B,1} \leq Y \leq cnt_{B,2}$ , $cnt_{C,1} \leq Y \leq cnt_{C,2}$ ，那么肯定存在至少一种填入的方案。理由如下：

构建一张二分图：

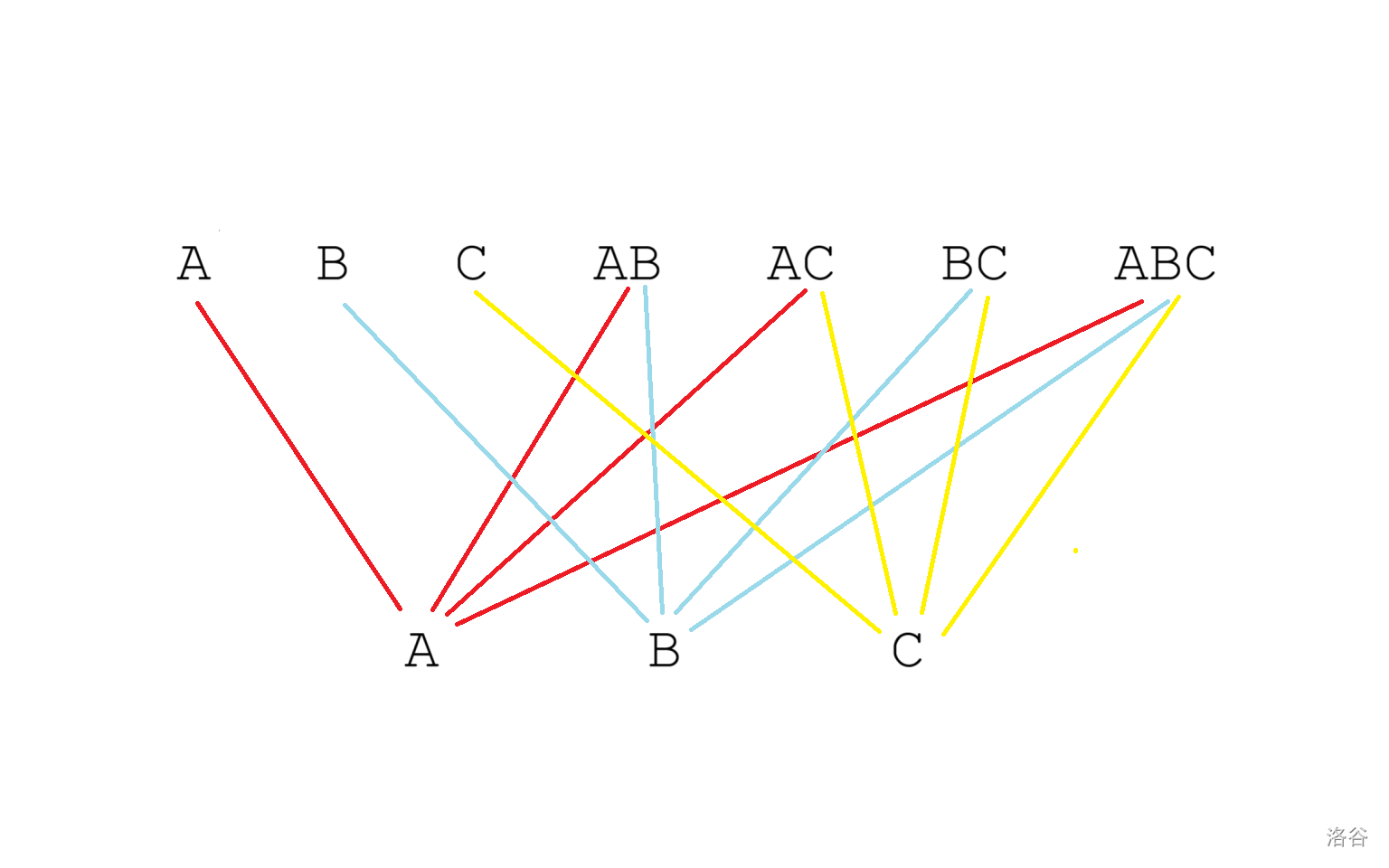
手玩Hall定理可得，这里不一一列举了。

现在我们随意钦定一个连续段的类型是其产生最小贡献的类型，例如 A...A 就是只能填入 A ；A...B 就是只能填入 AB 。接下来分类讨论：

对于三种字符都满足 $cnt_{A,2} \geq X$ ，BC 同理。

那么唯一的困扰就是形如 $cnt_{A,1} > X$ 的限制了，拿 A 举例，就是需要将某一些形如 A...A 的连续段填入 B 或者 C (这一点其实无所谓，因为都不会对 $cnt_{B,1},cnt_{C,1}$ 产生影响)。因为要最小化代价，那我们肯定选择长度尽量长的连续段进行转化了，二分即可，这是最简单的情况。

存在某一种连续段满足 $cnt_{A,2} < X$ , BC 同理。我们假设是 A 没有满足了 $cnt_{A,2} < X$。

第一个问题就是在 BC 中可能出现 $cnt_{B,1}>Y$ 和 $cnt_{C,1} > Z$ ，我们先贪心选取长度尽可能长的区间为 AB 和 AC （转化为 BC 在当下看来没有意义）。

接下来如果依然没有满足 $cnt_{A,2}< X$ ，就需要将进行如下三种转化了：

• B 转化为 AB ，代价为 $+2$ 。
• C 转化为 AC ，代价为 $+2$ 。
• BC 转化为 ABC ，代价为 $+1$ 。

我们先按照“性价比进行排序”，也就是单位代价的长度排序然后贪心选取。如果我们选取的单位代价最小的区间代价为 $+2$ ，就说明我们的解不一定是一个最优的解。但是最优解的贡献至多比我们当前解的贡献 $-1$ 。因为我们不可能将这个 $+2$ 的连续段完全删除且不进行任何添加获取一组解。

贡献 $-1$ 的可能性有两种。

• 将这个代价为 $+2$ 的去掉，然后添加一个代价为 $+1$ 的进来。

• 删掉我们已经添加的一个代价为 $+1$ 的解。

那么这种情况就可以完成了。这部分显然可以通过各种方式优化到只有一只 $\log$ 。我个人的实现方式并不好，这里就不丢人现眼了。

存在两个字符不满足形如 $cnt_{A,2} \geq X$ 的约束。我们假设只有 A 满足了这种约束。

那么我们就需要将 A 转化为 AB，AC，ABC 了。我要说明的是，如果将目前状态为 A 的连续段按照长度从大到小排序，选取一个尽可能短的前缀使得可以满足 $X \geq cnt_{A,1}$ 。那么我们只需要对这些连续段进行转化。

首先，这些连续段完全可以让我们能够进行转化使得有解，因为将他们全部都放到 ABC 就可以了。这样的代价是数量乘上 $3$ 吗？如果真的这样，我们追加一些 A 的连续段可能产生更优解才对啊。

假设我们有一个长度为 $len_1$ 的连续段 AB 或者 AC ，以及一个长度为 $len_2(len_1 \leq len_2)$ 的连续段 ABC 。实际上可以在形式上理解为存在一个长度为 $len_1+len_2$ 的连续段 ABC （注意是形式上不是贡献上）。我简单说明一下为什么：

首先，A 是可以随便填的，那么我们就优先填入长度为 $len_1$ 的段里面去。如果 $len_1$ 直接被塞满了，那么 BC 全部塞入长度为 $len_2$ 的连续段肯定是很好；如果没有被塞满，那么我们取准备填入的 BC 中数量较多者，肯定可以和 A 一起把长度为 $len_1$ 的连续段塞爆（鸽巢原理），剩余的全部填入长度为 $len_2$ 的即可。

有了这个结论，我们有一个骚操作。假设我们准备转化为 ABC 的连续段集合为 $S$ ，我们取 $S$ 中长度最大的一个转化为 ABC ，剩余的转化为 AB 。根据我们的结论，他们形式上等价于 ABC ，但是贡献上只有连续段数量的两倍多一。

我们知道，这个集合 $S$ 是让我们的 A 合法的最小集合，那么全部转化为 AB 或者 AC 而不转化为 ABC 的贡献——连续段数量的两倍就应该是答案的下界。我们最终的问题就是判断是否可以达到这个下届。这显然是一个背包问题。

我们需要对于 A 的连续段按照长度从大到小排序后的一个前缀，判断其是否可以组成一个大小在 $[L,R]$ 之间的数（假设将长度为 $x$ 的连续段转化为了 AB ，就需要满足 $cnt_{B,2}+x \geq Y$ ， $cnt_{C,2}+(sum-x) \geq Z$）。

你肯定可以bitset，这样时间复杂度是 $O(\frac{(n+q)n}{w}+(n+q)\log n)$ ，我写了也是过不了。

要判断一个前缀能否拼出一个区间 $[L,R]$ 内的数，我们从反方向考虑问题就是定义 $f_i$ 表示 $i$ 至少在哪个前缀被拼出来，那么就转化为了一个 rmq 问题，这是好解决的。对于 $f_i$ 的求解使用多重背包的队列优化就可以做到 $O(n\sqrt n)$ ,这点大家都会。

时间复杂度就可以做到 $O(n\sqrt n + (n+q)\log n)$ 。

#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read(){
	int x=0,f=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-f;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
	return x*f;
}
int buf[1<<10];
inline void print(int x,char ch=' '){
	if(x<0) putchar('-'),x=-x;
	int tot=0;
	do{
		buf[++tot]=x%10;
		x/=10;
	}while(x);
	for(int i=tot;i;i--)
		putchar(buf[i]+'0');
	putchar(ch);
}
const int MAXN=3e5+5,inf=1e9;
int n,delta;
char s[MAXN];

int tot[6],a[6][MAXN],b[6][MAXN];
bool cmp(int x,int y){
	return x>y;
}
int cnt[3];
void init(){
	for(int i=2;i<=n;i++){
		if(s[i]!='?'&&s[i-1]!='?')
			delta+=(s[i]!=s[i-1]); 
		if(s[i]=='?'&&s[i-1]!='?'){
			int l=i,r=i;
			while(r<n&&s[r+1]=='?') r++;
			
			if(s[l-1]==s[r+1]){
				if(s[l-1]=='A'){
					a[0][++tot[0]]=r-l+1;
					cnt[0]+=r-l+1;
				}
				else if(s[l-1]=='B'){
					a[1][++tot[1]]=r-l+1;
					cnt[1]+=r-l+1;
				}
				else{
					a[2][++tot[2]]=r-l+1;
					cnt[2]+=r-l+1;
				}
			}
			else{
				delta++;
				if((s[l-1]=='A'&&s[r+1]=='B')||(s[l-1]=='B'&&s[r+1]=='A')){
					a[3][++tot[3]]=r-l+1;
					cnt[0]+=r-l+1;
					cnt[1]+=r-l+1;
				}
				else if((s[l-1]=='A'&&s[r+1]=='C')||(s[l-1]=='C'&&s[r+1]=='A')){
					a[4][++tot[4]]=r-l+1;
					cnt[0]+=r-l+1;
					cnt[2]+=r-l+1;
				}
				else{
					a[5][++tot[5]]=r-l+1;
					cnt[1]+=r-l+1;
					cnt[2]+=r-l+1;
				}
			}
		}
	}
	
	for(int i=0;i<6;i++){
		sort(a[i]+1,a[i]+tot[i]+1,cmp);
		for(int j=1;j<=tot[i];j++)
			b[i][j]=b[i][j-1]+a[i][j];
	}
}

int Q,ans[MAXN];

int find(int op,int x){
	int l=1,r=tot[op];
	while(l<r){
		int mid=(l+r)>>1;
		if(b[op][mid]>=x) r=mid;
		else l=mid+1;
	}
	return l;
}
int solve1(int x,int y,int z){
	int ans=0;
	if(b[0][tot[0]]>x) ans+=find(0,b[0][tot[0]]-x);
	if(b[1][tot[1]]>y) ans+=find(1,b[1][tot[1]]-y);
	if(b[2][tot[2]]>z) ans+=find(2,b[2][tot[2]]-z);
	return ans<<1;
}

struct node{
	int val,w,id1,id2;
	bool friend operator<(const node &a,const node &b){
		return a.val*b.w>b.val*a.w;
	}
}temp[MAXN];
int num;
int mp[6][MAXN];

struct sgt{
	int mn1,mn2,mx1,mx2,sum,w;
	sgt(){
		mn1=mn2=inf;
		mx1=mx2=-inf;
		sum=w=0;
	}
	sgt friend operator+(sgt ls,sgt rs){
		sgt ans;
		ans.mn1=min(ls.mn1,rs.mn1);
		ans.mn2=min(ls.mn2,rs.mn2);
		ans.mx1=max(ls.mx1,rs.mx1);
		ans.mx2=max(ls.mx2,rs.mx2);
		ans.sum=ls.sum+rs.sum;
		ans.w=ls.w+rs.w;
		return ans; 
	}
}t[MAXN*30];
int ls[MAXN*30],rs[MAXN*30];
int rot[6][MAXN],res;
void pushup(int i){
	t[i]=t[ls[i]]+t[rs[i]];
}
void update(int &i,int j,int l,int r,int k,int val,int w){
	if(!i) i=++res;
	if(l==r){
		t[i].sum=val;
		if(w==1){
			t[i].mn1=t[i].mx1=val;
			t[i].w=1;
		}
		else{
			t[i].mn2=t[i].mx2=val;
			t[i].w=2;
		}
		return ;
	}
	int mid=(l+r)>>1;
	if(mid>=k){
		update(ls[i],ls[j],l,mid,k,val,w);
		rs[i]=rs[j];
	}
	else{
		update(rs[i],rs[j],mid+1,r,k,val,w);
		ls[i]=ls[j];
	}
	pushup(i);
}
int query(int r1,int r2,int r3,int l,int r,int sum){
	if(l==r) return l;
	int mid=(l+r)>>1,val;
	val=t[ls[r1]].sum+t[ls[r2]].sum+t[ls[r3]].sum;
	if(val>=sum)
		return query(ls[r1],ls[r2],ls[r3],l,mid,sum);
	return query(rs[r1],rs[r2],rs[r3],mid+1,r,sum-val);
}
sgt query(int r1,int r2,int r3,int l,int r,int L,int R){
	if(L<=l&&r<=R)
		return t[r1]+t[r2]+t[r3];
	int mid=(l+r)>>1;
	if(R<=mid)
		return query(ls[r1],ls[r2],ls[r3],l,mid,L,R);
	if(mid<L)
		return query(rs[r1],rs[r2],rs[r3],mid+1,r,L,R);
	return query(ls[r1],ls[r2],ls[r3],l,mid,L,mid)+
		   query(rs[r1],rs[r2],rs[r3],mid+1,r,mid+1,R);
}
int query(int r1,int r2,int r3,int sum){
	int pos=query(r1,r2,r3,1,n,sum);
	sgt L,R;
	L=query(r1,r2,r3,1,n,1,pos);
	R=query(r1,r2,r3,1,n,pos+1,n);
	int ans=L.w;
	if(L.sum-L.mn1>=sum) return ans-1;
	if(L.sum-L.mn2+R.mx1>=sum) return ans-1;
	return ans; 
}
int solve2(int x,int y,int z){
	int ans=0,pos0=0,pos1=0,pos2=0,delta=0; 
	if(x<b[0][tot[0]]){
		pos0=find(0,b[0][tot[0]]-x);
		ans+=pos0*2;
		delta+=b[0][pos0];
	}
	if(y<b[1][tot[1]]){
		pos1=find(1,b[1][tot[1]]-y);
		ans+=pos1*2;
		delta+=b[1][pos1];
	}
	if(z<b[2][tot[2]]){
		pos2=find(2,b[2][tot[2]]-z);
		ans+=pos2*2;
		delta+=b[2][pos2];
	}
	
	if(cnt[0]<x){
		if(cnt[0]+delta>=x) return ans;
		return ans+query(rot[1][pos1+1],rot[2][pos2+1],rot[5][1],x-cnt[0]-delta);
	}
	else if(cnt[1]<y){
		if(cnt[1]+delta>=y) return ans;
		return ans+query(rot[0][pos0+1],rot[2][pos2+1],rot[4][1],y-cnt[1]-delta);
	}
	else{
		if(cnt[2]+delta>=z) return ans;
		return ans+query(rot[0][pos0+1],rot[1][pos1+1],rot[3][1],z-cnt[2]-delta);
	}
}

int fst[3][MAXN],cpy[MAXN],dp[MAXN];
struct segment_tree{
	int t[MAXN<<2];
	void pushup(int i){
		t[i]=min(t[i<<1],t[i<<1|1]);
	}
	void update(int i,int l,int r,int k,int w){
		if(l==r){
			t[i]=w;
			return ;
		}
		int mid=(l+r-1)>>1;
		if(mid>=k)
			update(i<<1,l,mid,k,w);
		else
			update(i<<1|1,mid+1,r,k,w);
		pushup(i);
	}
	int query(int i,int l,int r,int L,int R){
		if(L<=l&&r<=R) return t[i];
		int mid=(l+r-1)>>1;
		if(R<=mid)
			return query(i<<1,l,mid,L,R);
		if(mid<L)
			return query(i<<1|1,mid+1,r,L,R);
		return min(query(i<<1,l,mid,L,mid),query(i<<1|1,mid+1,r,mid+1,R)); 
	}
}tr[3];
int query(int op,int l,int r){
	if(l>r) return inf;
	return tr[op].query(1,0,n,l,r);
}
void solve3(){
	for(int i=0;i<3;i++){
		for(int j=0;j<=n;j++){
			fst[i][j]=inf;
			dp[j]=0;
		}
		fst[i][0]=0,dp[0]=1;
		
		for(int j=1;j<=tot[i];j++){
			if(a[i][j]!=a[i][j-1]){
				int l=j,r=j,len;
				while(r<tot[i]&&a[i][r+1]==a[i][j]) r++;
				len=r-l+1;
				
				for(int k=0;k<=n;k++) cpy[k]=dp[k];
				for(int mod=0;mod<a[i][j];mod++){
					int lst=-1;
					for(int k=mod;k<=n;k+=a[i][j]){
						if(cpy[k]) lst=k;
						if(lst!=-1&&!dp[k]&&(k-lst)/a[i][j]<=len){
							dp[k]=1;
							fst[i][k]=j+(k-lst)/a[i][j]-1;
						}
					}
				}
			}
		}
		
		for(int j=0;j<=n;j++) tr[i].update(1,0,n,j,fst[i][j]);
	}
}
int solve3(int x,int y,int z){
	if(cnt[0]>=x){
		int pos=find(0,b[0][tot[0]]-x),ans=pos*2+1;
		if(query(0,y-cnt[1],cnt[2]+b[0][pos]-z)<=pos) ans--;
		return ans;
	}
	else if(cnt[1]>=y){
		int pos=find(1,b[1][tot[1]]-y),ans=pos*2+1;
		if(query(1,x-cnt[0],cnt[2]+b[1][pos]-z)<=pos) ans--; 
		return ans;
	}
	else{
		int pos=find(2,b[2][tot[2]]-z),ans=pos*2+1;
		if(query(2,x-cnt[0],cnt[1]+b[2][pos]-y)<=pos) ans--;
		return ans;
	}
}
signed main(){
//	freopen("tritium.in","r",stdin);
//	freopen("tritium.out","w",stdout);
	n=read();
	scanf("%s",s+1);
	init();
	
	for(int i=0;i<6;i++){
		for(int j=1;j<=tot[i];j++){
			++num;
			temp[num].val=a[i][j];
			if(i<3) temp[num].w=2;
			else temp[num].w=1;
			temp[num].id1=i,temp[num].id2=j;
		}
	}
	sort(temp+1,temp+num+1);
	
	for(int i=1;i<=num;i++)
		mp[temp[i].id1][temp[i].id2]=i;
	for(int i=0;i<6;i++)
		for(int j=tot[i];j>=1;j--)
			update(rot[i][j],rot[i][j+1],1,n,mp[i][j],a[i][j],1+(i<3));
		
	
	Q=read();
	solve3();
	for(int i=1;i<=Q;i++){
		int x=read(),y=read(),z=read();
		
		if(cnt[0]>=x&&cnt[1]>=y&&cnt[2]>=z){
			ans[i]=solve1(x,y,z);
			continue;
		}
		
		int op=(cnt[0]<x)+(cnt[1]<y)+(cnt[2]<z);
		if(op==1){
			ans[i]=solve2(x,y,z);
			continue;
		}
		
		ans[i]=solve3(x,y,z);
	}
	
	for(int i=1;i<=Q;i++) print(ans[i]+delta,'\n');
	return 0;
}