自动搬运

查看原文

来自洛谷，原作者为

	yes_NT 正逆的转换从未停止，前方是毁灭亦是重生

搬运于2025-08-24 23:11:28，当前版本为作者最后更新于2025-05-21 19:59:06，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

P11933

乍一看这题似乎不好做，因为我们貌似不能每次精确找到路的折点。然而我们进而可以考虑路和河流有什么神秘的关系（？

这里给出结论：路的折点一定也是河流的折点。

证明：假设我们现在已经知道路与河流每一个折点的位置关系，也就是说我们已经知道了路与河流的交点情况，要使得总代价最小，我们只需要让路径长度最小即可。

而我们不难发现，通过不断调整，一定可以使得路径贴在河流的折点上，我们要保证交点情况不变的前提下，是不可以绕过河流的，因此路的折点一定也是河流的折点。

知道了这个结论，我们可以考虑怎么转移了。记 $f_{i,0/1}$ 表示在河流折点 $i$ 处的左/右两侧作为修到 $i$ 处的路的最短路径，那么对于相邻的节点，有

$$\begin{aligned} &f_{i,0}\gets f_{i-1,0}+dis(i-1,i)\\ &f_{i,0}\gets f_{i-1,1}+dis(i-1,i)+T\\ &f_{i,1}\gets f_{i-1,1}+dis(i-1,i)\\ &f_{i,1}\gets f_{i-1,0}+dis(i-1,i)+T\\ \end{aligned}$$

其中 $dis(i,j)$ 表示 $i$ 点与 $j$ 点的距离。

而对于不相邻的节点，我们就要考虑两个节点之间连线穿过的线段数量了。记 $g_{i,j}$ 表示 $i$ 与 $j$ 点的连线经过了的河流的数量（不包括 $(i,i-1)$ 与 $(j,j+1)$ 的河流）。然而，只知道这个，我们是不能直接转移的，因为我们不难发现，连线之间的转移是有可能与上述相邻的两条河流产生交点的。

这里以 $f_{j,0}$ 转移到 $f_{i,0}$ 为例。

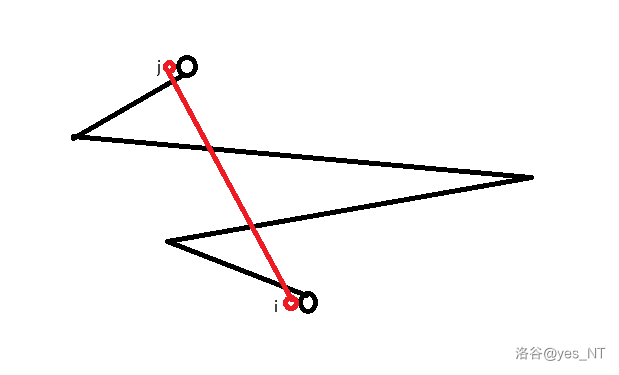
如上图，路径与 $(i,i-1)$ 和 $(j,j+1)$ 都有交点，因此我们需要单独判断交点的情况。如果判断 $(i,j)$ 与 $(i,i-1)$ 是否产生了交点，我们可以通过判断这两条线的斜率的情况，通过比较斜率进而得出是否产生了额外的交点。

剩下的 $3$ 个方向也可以通过类似的方式解决，至此，我们可以写出以下的转移过程。

    f[1][0] = f[1][1] = 0;
    for (int i = 2; i <= n; ++i) {
        for (int j = 1; j < i - 1; ++j) {
            f[i][0] = min(f[i][0], dis(i, j) + f[j][0] + T * (g[j][i] + (k(i, j) > k(j + 1, j)) + (k(i, j) < k(i, i - 1))));
            f[i][0] = min(f[i][0], dis(i, j) + f[j][1] + T * (g[j][i] + (k(i, j) < k(j + 1, j)) + (k(i, j) < k(i, i - 1))));
            f[i][1] = min(f[i][1], dis(i, j) + f[j][1] + T * (g[j][i] + (k(i, j) < k(j + 1, j)) + (k(i, j) > k(i, i - 1))));
            f[i][1] = min(f[i][1], dis(i, j) + f[j][0] + T * (g[j][i] + (k(i, j) > k(j + 1, j)) + (k(i, j) > k(i, i - 1))));
        }
        f[i][0] = min(f[i][0], dis(i - 1, i) + f[i - 1][0]);
        f[i][0] = min(f[i][0], dis(i - 1, i) + f[i - 1][1] + T);
        f[i][1] = min(f[i][1], dis(i - 1, i) + f[i - 1][1]);
        f[i][1] = min(f[i][1], dis(i - 1, i) + f[i - 1][0] + T);
        // printf("%.7lf %.7lf\n", f[i][0], f[i][1]);
    }

如果暴力算 $g_{i,j}$，现在代码的时间复杂度是 $O(n^3)$ 级别的。

考虑怎么快速计算这一过程，不难发现如果 $IJ$ 与 河流 $AB$ 产生了交点，$IJ$ 的斜率一定在 $BI$ 和 $AI$ 之间，因为我们只需要考虑 $i$ 和 $j$ 之间的节点。

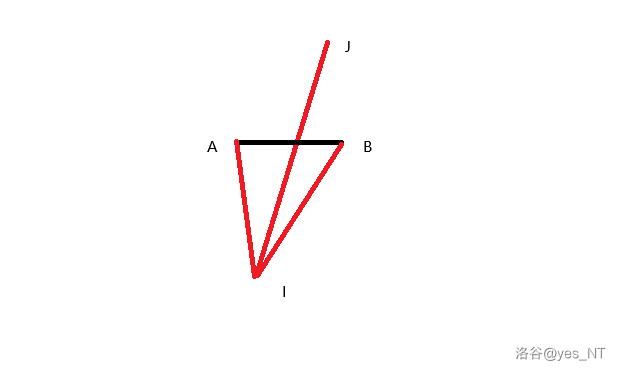
于是我们可以用线段树维护这一过程，插入河流时就在对应位置做区间加，单点查询路径的斜率即可。

至此我们完成了这道题。

时间复杂度 $O(n^2\log n)$ 。

Code

#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
template<typename T> inline void read(T &x) {
    x = 0; bool f = 0; char c = getchar();
    while (c < '0' || c > '9') {if (c == '-') f = 1; c = getchar();}
    while (c >= '0' && c <= '9') x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();
    if (f) x = ~x + 1;
}
const int N = 2005;
int dat[N << 2];
void pushdown(int p) {
    dat[p * 2] += dat[p];
    dat[p * 2 + 1] += dat[p];
    dat[p] = 0;
}
void update(int p, int l, int r, int L, int R, int v) {
    if (L > R)
        swap(L, R);
    if (L <= l && r <= R) {
        dat[p] += v;
        return;
    }
    pushdown(p);
    int mid = (l + r) >> 1;
    if (L <= mid)
        update(p * 2, l, mid, L, R, v);
    if (mid < R)
        update(p * 2 + 1, mid + 1, r, L, R, v);
}
int query(int p, int l, int r, int x) {
    if (l == r)
        return dat[p];
    pushdown(p);
    int mid = (l + r) >> 1;
    if (x <= mid)
        return query(p * 2, l, mid, x);
    return query(p * 2 + 1, mid + 1, r, x);
}
const double inf = 1000000000.0;
int n, g[N][N], cnt;
double T, a[N], f[N][2], x[N], y[N], aa[N];
double dis(int i, int j) {
    return sqrt(1.0 * (x[i] - x[j]) * (x[i] - x[j]) + 1.0 * (y[i] - y[j]) * (y[i] - y[j]));
}
double k(int i, int j) {
    return (double)(x[j] - x[i]) / (double)(y[j] - y[i]);
}
int main() {
    memset(f, 0x7f, sizeof(f));
    read(n); scanf("%lf", &T);
    for (int i = 1; i <= n; ++i) {
        scanf("%lf%lf", &x[i], &y[i]);
    }
    for (int i = 1; i <= n; ++i) {
        cnt = 0;
        for (int j = 1; j < i; ++j) {
            a[++cnt] = k(i, j);
            aa[cnt] = a[cnt];
        }
        sort(aa + 1, aa + cnt + 1);
        for (int j = 1; j <= cnt; ++j)
            a[j] = lower_bound(aa + 1, aa + cnt + 1, a[j]) - aa;
        for (int j = 1; j < cnt; ++j)
            update(1, 1, cnt, a[j], a[j + 1], 1);
        for (int j = 1; j < cnt; ++j) {
            update(1, 1, cnt, a[j], a[j + 1], -1);
            g[j][i] = query(1, 1, cnt, a[j]);
        }
    }
    f[1][0] = f[1][1] = 0;
    for (int i = 2; i <= n; ++i) {
        for (int j = 1; j < i - 1; ++j) {
            f[i][0] = min(f[i][0], dis(i, j) + f[j][0] + T * (g[j][i] + (k(i, j) > k(j + 1, j)) + (k(i, j) < k(i, i - 1))));
            f[i][0] = min(f[i][0], dis(i, j) + f[j][1] + T * (g[j][i] + (k(i, j) < k(j + 1, j)) + (k(i, j) < k(i, i - 1))));
            f[i][1] = min(f[i][1], dis(i, j) + f[j][1] + T * (g[j][i] + (k(i, j) < k(j + 1, j)) + (k(i, j) > k(i, i - 1))));
            f[i][1] = min(f[i][1], dis(i, j) + f[j][0] + T * (g[j][i] + (k(i, j) > k(j + 1, j)) + (k(i, j) > k(i, i - 1))));
        }
        f[i][0] = min(f[i][0], dis(i - 1, i) + f[i - 1][0]);
        f[i][0] = min(f[i][0], dis(i - 1, i) + f[i - 1][1] + T);
        f[i][1] = min(f[i][1], dis(i - 1, i) + f[i - 1][1]);
        f[i][1] = min(f[i][1], dis(i - 1, i) + f[i - 1][0] + T);
        // printf("%.7lf %.7lf\n", f[i][0], f[i][1]);
    }
    printf("%.7lf", min(f[n][0], f[n][1]));
    return 0;
}