1 条题解
-
0
自动搬运
来自洛谷,原作者为

EuphoricStar
Remember.搬运于
2025-08-24 23:11:22,当前版本为作者最后更新于2025-03-26 22:31:04,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
比较有趣的题。
首先考虑固定一个 怎么 check 是否合法。一个比较暴力的想法是枚举每个人的睡觉先后顺序,然后从前往后按照先后顺序确定每个人可能的最早的睡觉时间。
题目要求最大化 ,一个自然的想法是考虑二分。可以证明最优解的分子 且分母 ,感性理解就是,最优解的形式一定能调整成,每个人睡觉的区间端点要么是整数,要么顶着另一个人睡觉的区间端点。所以我们枚举出所有分数然后对分数序列二分即可。
接下来我们解决 check 的复杂度问题。第一个问题是,确定了一个前缀的人的睡觉区间之后,如何快速确定下一个人可能的最早睡觉时间。首先一个限制是睡觉的区间长度 ,且这一段除了这个人以外,还至少有一个人空闲。然后是不能出现没有人空闲的时刻,那么我们把上一个人睡觉区间分成若干段。对于被覆盖了 次的段,设段内最晚的空闲人数 的时刻为 ,那么这个人的睡觉时间一定在 之后。例如:
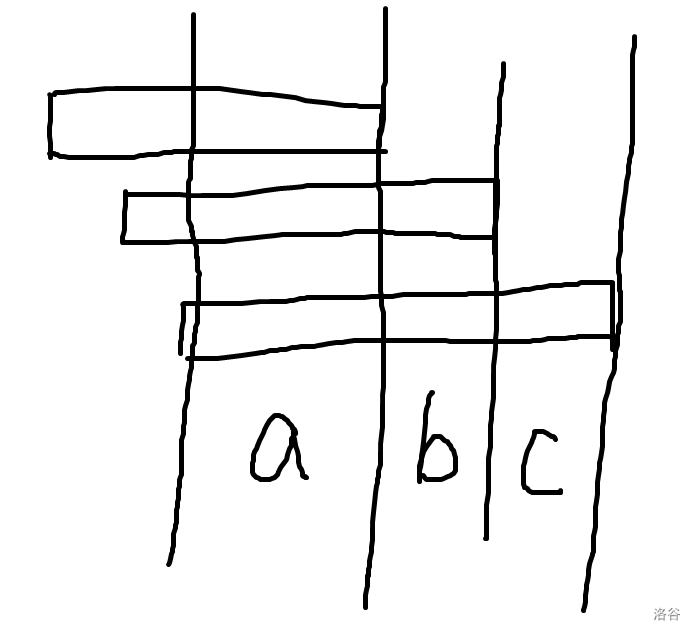
我们要找到 段最晚的空闲人数 的时刻, 段最晚的空闲人数 的时刻, 段最晚的空闲人数 的时刻。这部分可以通过合理地预处理,做到 确定下一个人可能的最早睡觉时间。
第二个问题是,我们显然不能 地枚举全排列。看到 的数据范围我们一般会考虑状压 dp,但是这题状压之后 dp 状态不好设计。
接下来就是这题的神奇之处了。假设我们前面已经选了一些人睡觉,考虑求出每个还没选的人的最早睡觉时间,那么下一个睡觉的人只会在时间最小值和次小值当中选。证明大概就是,如果我们选了第三小值或者之后的人睡觉,那么一定还能选最小值的人睡觉:
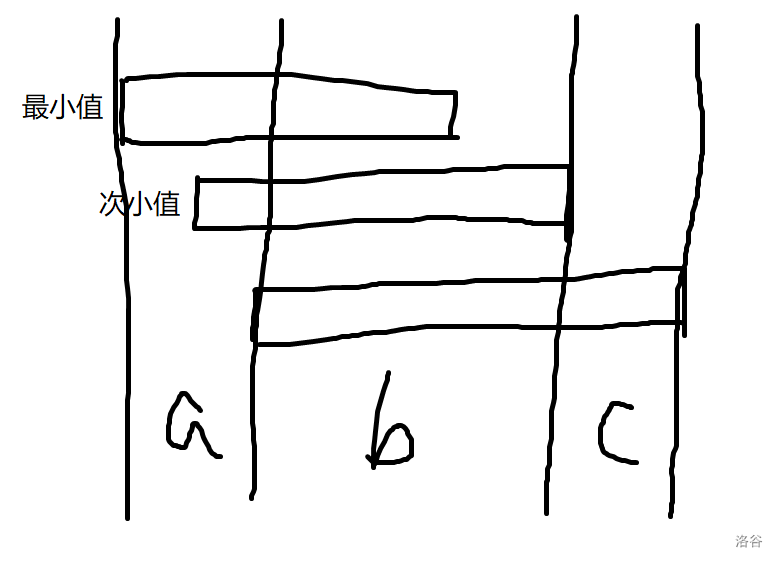
考虑若选了最小值和第三小值的人睡觉,且没有选次小值睡觉。那么 段和 段已经合法。考虑 段,发现次小值的人一定空闲,所以也合法。
所以我们每次枚举两个决策点再继续 dfs 即可。这样就把原来的 枚举全排列变成了 。
时间复杂度 $O(n(l + \sum\limits_{i = 0}^n (n - i) 2^i) \log(nl)) = O((2^n + l) n \log(nl))$。注意睡觉区间端点都可能是分数,所以有一定的代码细节。
// Problem: P11921 [PA 2025] 看护 / Opieka // Contest: Luogu // URL: https://www.luogu.com.cn/problem/P11921 // Memory Limit: 1 MB // Time Limit: 5000 ms // // Powered by CP Editor (https://cpeditor.org) #include <bits/stdc++.h> #define pb emplace_back #define fst first #define scd second #define mkp make_pair #define mems(a, x) memset((a), (x), sizeof(a)) using namespace std; typedef long long ll; typedef double db; typedef unsigned long long ull; typedef long double ldb; typedef pair<ll, ll> pii; const int maxn = 100100; int n, m, a[19][maxn], b[maxn], pre[19][maxn], c[19][maxn]; pii fr[maxn << 5]; char s[19][maxn]; int p[19]; ll X, Y, f[19]; bool dfs(int d, int S) { if (d == n + 1) { return 1; } vector<int> cur; for (int i = 1; i <= n; ++i) { if (!(S & (1 << i))) { cur.pb(i); } } pii mn(1e18, 0), smn(1e18, 0); for (int i : cur) { ll t = f[d - 1]; for (int j = 1; j < d; ++j) { ll l = max(f[d - 1], j == 1 ? 0LL : f[j - 1] + X), r = f[j] + X; if (l < r) { if (b[(r + Y - 1) / Y] <= d - j + 1) { t = max(t, r); } else if (pre[d - j + 1][(r + Y - 1) / Y] * Y >= l) { t = max(t, pre[d - j + 1][(r + Y - 1) / Y] * Y); } } } if (t % Y) { if (a[i][t / Y + 1] >= (t + X + Y - 1) / Y - t / Y) { pii x(t, i); if (x < mn) { smn = mn; mn = x; } else if (x < smn) { smn = x; } continue; } else { t += Y - t % Y; } } t = (c[i][t / Y + 1] - 1) * Y; if (t == m * Y) { return 0; } pii x(t, i); if (x < mn) { smn = mn; mn = x; } else if (x < smn) { smn = x; } } f[d] = mn.fst; p[d] = mn.scd; if (dfs(d + 1, S | (1 << mn.scd))) { return 1; } if (smn.scd) { f[d] = smn.fst; p[d] = smn.scd; if (dfs(d + 1, S | (1 << smn.scd))) { return 1; } } return 0; } inline bool check(ll x, ll y) { for (int i = 1; i <= n; ++i) { c[i][m + 1] = m + 1; for (int j = m; j; --j) { c[i][j] = (a[i][j] * y >= x ? j : c[i][j + 1]); } } X = x; Y = y; f[0] = 0; return dfs(1, 0); } void solve() { scanf("%d%d", &n, &m); for (int i = 1; i <= n; ++i) { scanf("%s", s[i] + 1); for (int j = 1; j <= m; ++j) { b[j] += (s[i][j] == '.'); } } for (int i = 1; i <= m; ++i) { bool fl = 1; for (int j = 1; j <= n && fl; ++j) { fl &= (s[j][i] == 'X'); } if (fl) { puts("-1"); return; } } for (int i = 1; i <= n; ++i) { for (int j = m; j; --j) { a[i][j] = (s[i][j] == '.' && b[j] >= 2 ? a[i][j + 1] + 1 : 0); } } for (int i = 1; i <= n; ++i) { for (int j = 1; j <= m; ++j) { pre[i][j] = (b[j] <= i ? j : pre[i][j - 1]); } } int tot = 0; for (int i = 1; i <= m; ++i) { for (int j = 1; j <= n; ++j) { if (__gcd(i, j) == 1) { fr[++tot] = mkp(i, j); } } } sort(fr + 1, fr + tot + 1, [&](const pii &a, const pii &b) { return a.fst * b.scd < b.fst * a.scd; }); int l = 1, r = tot, ans = -1; while (l <= r) { int mid = (l + r) >> 1; if (check(fr[mid].fst, fr[mid].scd)) { ans = mid; l = mid + 1; } else { r = mid - 1; } } if (ans == -1) { puts("0/1"); return; } printf("%lld/%lld\n", fr[ans].fst, fr[ans].scd); } int main() { int T = 1; // scanf("%d", &T); while (T--) { solve(); } return 0; }
- 1
信息
- ID
- 11705
- 时间
- 5000ms
- 内存
- 1024MiB
- 难度
- 7
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
