自动搬运

查看原文

来自洛谷，原作者为

	bamboo12345 <-状态

搬运于2025-08-24 23:11:14，当前版本为作者最后更新于2024-10-05 15:41:40，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

原本这里是一道简单题的，但是因为本人突然有灵感出了这道题，恶心了别人，也狠狠地恶心了自己。

作为被小 e 评价创新程度 < A 的题，这个题确实比较烂，求轻喷（）。

---

题目描述：很形式化了，自己看吧。

做法：

我们分部分分一档档讲解。

首先注意到一个观察，如果我们要求 $f(l,r)$，那么肯定是每次从 $l$ 贪心选尽量长的一段，因为如果不选最长的，那么后面的限制就更难满足，这个稍微意会一下很简单。

测试点 1~3（12pts）

模拟这个观察，每次暴力到 $s$ 中找是否出现，而每次找到一个强制限定的位置，就直接截断新开一段就可以了。

强制限定操作打标记即可，赋值操作直接模拟。

复杂度 $O(Mnq)$。

测试点 4，12（8pts）

这个给的很良心了，也有助于出正解的一档部分分，这组部分分的特点在于 $V\le 10^9$。当然实际的时候因为保证有解，$V$ 与 $M$ 其实是同阶的。

结论是 $f(l,r) = r-l+1$，因为我们保证了数据随机，所以导致其实很难出现连续两项在 $s$ 中出现过。

注意到这个数据随机，对于做法会很有用。

测试点 4~11（32pts）

这几个数据点的限制在于 $n,M,q,T\le10^3,V\le10^9$，复杂度肯定是 $O(nq)$ 的。

那么我们发现 $O(Mnq)$ 的瓶颈在于我们需要每次都要到 $s$ 中匹配，我们考虑能不能 $O(1)$ 实现这个东西。实际上，可以用哈希或者广义 SAM 去优化这个过程。

测试点 5，13，14（12pts）

这几个数据点的限制在于没有 1，2 操作，也就意味着没有修改，只有询问。

我们发现，每次我们对于一个 $l$，他每次肯定都会跳到固定的一个位置然后重新开一段。所以我们这里，我们记 $nxt_l$ 代表满足 $[l,nxt_l-1]$ 在 $s$ 中出现而 $[l,nxt_l]$ 没有的那一个位置（对于 $[l,n]$ 在 $s$ 中出现过的，$nxt_l=n+1$）。

测试点 5 可以直接暴力按这个东西模拟，但是对于 13，14，我们需要用 SAM 预处理出来这个 $nxt$ 数组，或者注意到其实匹配的长度不多，直接预处理长度比较小比如小于等于 20 的子串的哈希也可以，然后可以用倍增处理出问题答案。记 $to_{i,j}$ 表示 $i$ 后跳 $2^j$ 后会到哪里，每次尝试跳多大一步就可，复杂度 $O(q\log n)$。

测试点 6~7，15~17（20pts）

这几个数据点的限制在于没有 2 操作。

我们注意到一件事情，如果 $l\le p<r$，则 $f(l,r)=f(l,p)+f(p+1,r)$，这启示我们，可以先按照强制限定的这些位置，把序列切成很多块，再进行计算。

比如这里，长为 10 的数组中，我们切分了 4，6 的位置，那么计算 $f(3, 8)$ 时，我们就会等同于计算 $f(3,4)+f(5,6)+f(7,8)$。

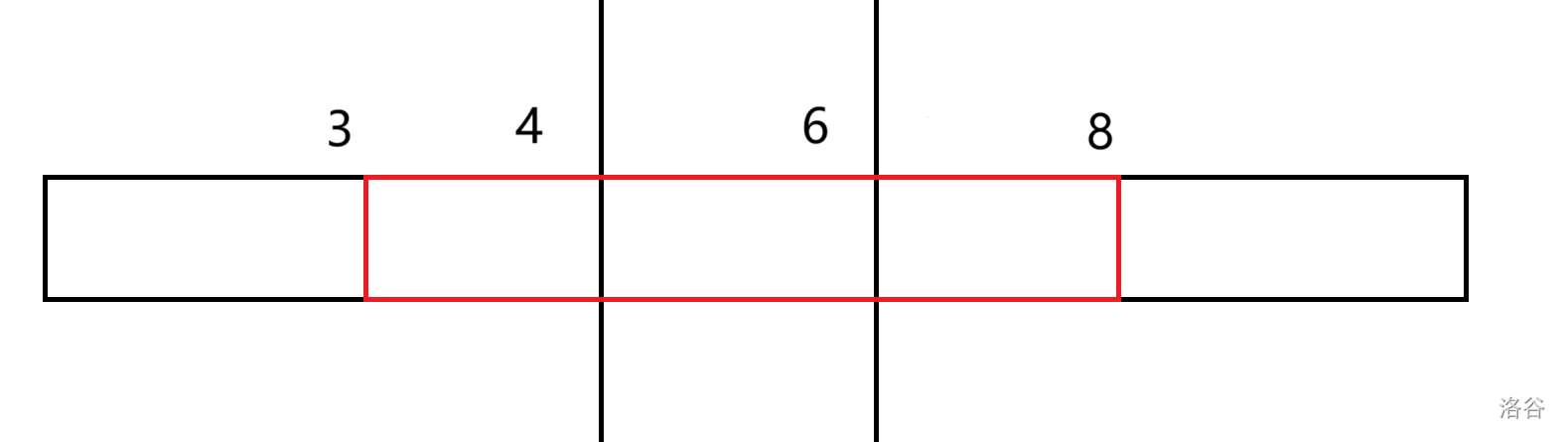
那么我们发现，我们询问的答案肯定是两端的散块加上中间强制限定切出来的整块，我们就可以维护这些切出来的整块的答案，然后散块重新计算。

具体的，我们可以用一个 set 维护强制限定的位置，然后每个 $p$ 维护 $[p+1,q]$ 这个区间的答案，$q$ 是 $p$ 在 set 里的后驱。然后开一个树状数组维护这些整块的贡献，就可以快速计算中间这些整块的答案。

复杂度 $O(q\log n)$。

测试点 1~25（100pts）

终于要到正解了，你会发现暴力打满其实有 68 分，很不错了。

我们发现，如果仅仅是用倍增维护 $nxt$ 的话，根本做不了这个修改这件事情，因为涉及的修改量太多了，你需要把 $[1,r]$ 的全部重构，复杂度爆炸。

首先我们观察到一件事情，对于直接的 $nxt$ 变化的，其实只有 $[max(l-50,1),r]$ 这个区间，因为数据随机，所以出现的概率在长度为 50 的情况下其实也是很小的，但是为了保险，我们取 $l-50$ 作为下限。那么总共所有修改的 $nxt$ 变化量就是 $O(n)$ 的。

那么我们其实可以想到这个题 弹飞绵羊。我们也是类似的做法，进行分块。这里也可以用 LCT 直接做，但是我不太会写我觉得常数比较大，并且我喜欢根号数据结构。我们直接重构这些修改的块即可。

然后也是类似于 弹飞绵羊 一题，我们维护跳到下一个块的位置和次数，对于询问先跳到相同的块，再暴力跳即可。

做完了吗？其实没有，这个也在我自己写 std 的时候坑了我一下。我们注意到，对于修改的时候，我们还需要把强制限定的整块的贡献更新，这样整个题就做完了。

简单的分析一下复杂度，维护强制限定是 $O(\sqrt n)$ 的（因为需要求相邻两项的 $f$），修改是均摊 $O(\sqrt n)$ 的，询问也是 $O(\sqrt n)$ 的，总的复杂度为 $O(q\sqrt n)$。

可以使用 lct 来做到 $O(\log n)$ 的复杂度，这里细说一下。考虑我们等于要对于一个端点 $l$ 我们需要求出来第一个跳到比 r 大的位置，这个东西等于我们先 access $l$ 这个节点，然后询问这一条链上第一个大于 r 的位置，这个就是个查后继就行了，可以做到理论一只 $\log$，但是对于常数就未知了（）。

当然用一些其他的数据结构比如线段树之类的也很容易做到 $O(\log^2 n)$ 的复杂度。

---

值得一提的是，发现很多选手写的都是 hash 维护出现的段数，这样也是可以的，就是空间会多个 $\log$，当然其实也没有多大。

代码：

#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x & (-x))
const int maxn = 2e5 + 5;
int n, q, m, l[maxn], r[maxn], pos[maxn], len;
int nxt[maxn], nxtb[maxn], dis[maxn];
int t[maxn];
struct node {
	map<int, int> nxt;
	int lnk, len;
};
struct SAM { // SAM，用来处理 nxt 
	node tr[maxn];
	int lst = 1, tot = 1;
	void add(int c) {
		int cur = ++tot, p = lst;
		tr[cur].len = tr[p].len + 1;
		while(p && !tr[p].nxt[c])
			tr[p].nxt[c] = cur, p = tr[p].lnk;
		if(!p)
			tr[cur].lnk = 1;
		else {
			int q = tr[p].nxt[c];
			if(tr[p].len + 1 == tr[q].len)
				tr[cur].lnk = q;
			else {
				int clone = ++tot;
				tr[clone] = tr[q], tr[clone].len = tr[p].len + 1;
				while(p && tr[p].nxt[c] == q)
					tr[p].nxt[c] = clone, p = tr[p].lnk;
				tr[cur].lnk = tr[q].lnk = clone;
			}
		}
		lst = cur;
	}
} sam;
void init() { // 处理 nxt 
	int p = 1, len = 0, ps = 1;
	for (int i = 1; i <= n; i++) {
		if(len) { // 减去 i - 1 
			if(sam.tr[sam.tr[p].lnk].len + 1 == len) // 考虑会不会移动节点 
				p = sam.tr[p].lnk;
			len--;
		}
		while(ps <= n && sam.tr[p].nxt[t[ps]]) //如果能往后 
			len++, p = sam.tr[p].nxt[t[ps]], ps++;
		nxt[i] = i + len; // [i, i + len - 1] 是一段，跳到 i + len 
	}
}
struct Tree_array {
	int tr[maxn], n;
	void add(int x, int val) {
		while(x <= n)
			tr[x] += val, x += lowbit(x);
	}
	int query(int x) {
		int ans = 0;
		while(x)
			ans += tr[x], x -= lowbit(x);
		return ans;
	}
} tree;
void build() { // 分块 
	len = sqrt(n);
	if(n <= 50)
		len = n;
	else
		len = max(len, 50);
	for (int i = 1; i <= n; i++) {
		pos[i] = (i - 1) / len + 1;
		if(!l[pos[i]])
			l[pos[i]] = i;
		r[pos[i]] = i;
	}
} 
void buildblock(int p) {// 重构编号为 p 的块
 	for (int i = r[p]; i >= l[p]; i--) {
 		if(nxt[i] > r[p])
 			nxtb[i] = nxt[i], dis[i] = 1;
 		else
 			nxtb[i] = nxtb[nxt[i]], dis[i] = dis[nxt[i]] + 1;
	}
}
int queryin(int l, int r) { //询问区间中无强制限定的答案 
	if(l > r)
		return 0;
	int p = pos[l], q = pos[r], ans = 0, nw = l;
	for (int i = p; i < q; i++)
		ans += dis[nw], nw = nxtb[nw];
	while(nw <= r) 
		ans++, nw = nxt[nw];
	return ans;
}
int val[maxn];
set<int> s;
int queryall(int l, int r) { // 询问区间中有强制限定的答案 
	set<int>::iterator itl = s.lower_bound(l), itr = s.lower_bound(r);
	itr--;
	if(*itl >= r)
		return queryin(l, r);
	int ans = queryin(l, *itl) + queryin(*itr + 1, r);
	if(*itl == *itr)
		return ans;
	itr--;
	return ans + tree.query(*itr + 1) - tree.query(*itl); 
}
void add(int x) { // 加入一个强制限定 
	set<int>::iterator itl = s.lower_bound(x), itr = s.upper_bound(x);
	itl--; 
	// 清除 [l+1,r]，加入 [l+1,x],[x+1,r] 
	tree.add(*itl + 1, -val[*itl + 1]);
	val[*itl + 1] = queryin(*itl + 1, x);
	tree.add(*itl + 1, val[*itl + 1]);
	val[x + 1] = queryin(x + 1, *itr);
	tree.add(x + 1, val[x + 1]);
	s.insert(x);
}
void del(int x) { // 删除一个强制限定 
	set<int>::iterator it = s.find(x), itl = it, itr = it;
	itl--, itr++;
	tree.add(x + 1, -val[x + 1]);
	val[x + 1] = 0;
	tree.add(*itl + 1, -val[*itl + 1]);
	val[*itl + 1] = queryin(*itl + 1, *itr);
	tree.add(*itl + 1, val[*itl + 1]);
	s.erase(x);
}
int t0[maxn], id;
void renew(int l, int r) { // 因为 nxt 更新了，所以也要重新维护 set 的贡献 
	set<int>::iterator itl = s.lower_bound(l), itr = itl;
	itl--;
	while(*itl < r) {
		tree.add(*itl + 1, -val[*itl + 1]);
		val[*itl + 1] = queryin(*itl + 1, *itr);
		tree.add(*itl + 1, val[*itl + 1]);
		itl++, itr++;
	}
}
void change(int l, int r) {
	for (int i = l; i <= r; i++)
		t[i] = t0[i];
	l = max(l - 50, 1);
	int p = 1, len = 0, ps = l;
	for (int i = l; i <= r; i++) { // 类似预处理 
		if(len) {
			if(sam.tr[sam.tr[p].lnk].len + 1 == len)
				p = sam.tr[p].lnk;
			len--;
		}
		while(ps <= n && sam.tr[p].nxt[t[ps]]) 
			len++, p = sam.tr[p].nxt[t[ps]], ps++;
		nxt[i] = i + len; 
	}
	for (int i = pos[l]; i <= pos[r]; i++)
		buildblock(i);
	renew(l, r);
}
int read() {
	int sum = 0;
	char c = getchar();
	while(!isdigit(c))
		c = getchar();
	while(isdigit(c))
		sum = sum * 10 + c - '0', c = getchar();
	return sum;
}
void write(int x) {
	if(x <= 9) {
		putchar(x + '0');
		return ;
	}
	write(x / 10);
	putchar(x % 10 + '0');
}
int main() {
// 	freopen("test.in", "r", stdin);
// 	freopen("baoli.out", "w", stdout);
	int V = 0;
	n = read(), m = read(), q = read(), id = read();
	for (int i = 1; i <= m; i++) {
		int k = read();
		sam.lst = 1;
		for (int j = 1; j <= k; j++) {
			int x = read();
			sam.add(x);
			V = max(V, x);
		}
	}
	for (int i = 1; i <= n; i++)
		t[i] = read(), V = max(V, t[i]); 
	init(), tree.n = n;
	build();
	for (int i = pos[1]; i <= pos[n]; i++)
		buildblock(i);
	s.insert(0), s.insert(n); // 插入 0，n，防爆 
	while(q--) {
		int op = read();
		if(op == 1) { // 限定 
			int x = read();
			if(val[x + 1])
				del(x);
			else
				add(x);
		}
		if(op == 2) { // 修改 
			int l, r;
			l = read(), r = read();
			while(l > r);
			for (int i = l; i <= r; i++)
				t0[i] = read();
			change(l, r);
		}
		if(op == 3) { // 询问 
			int l, r;
			l = read(), r = read();
			while(l > r);
			write(queryall(l, r));
			putchar('\n');
		}
	}
	return 0;
}