自动搬运

查看原文

来自洛谷，原作者为

	ailanxier 练习c++三年多的大四退役?

搬运于2025-08-24 21:22:13，当前版本为作者最后更新于2020-08-24 21:37:43，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

  在博客中观看

题意概述

  根据规则绘制一棵被删去部分节点的满二叉树。节点用 $o$ 表示，树枝用/\表示。每一层树枝长度会变化，以满足叶子结点有如下特定：

• 相邻叶子节点是兄弟节点（同一个父亲）时，间隔 $3$ 个空格。
• 相邻叶子节点不是兄弟节点，之间隔一个空格。

  一棵层数为 $4$ 的满二叉树长这样（可能会出现因为字符宽度不一而出现偏移）：

           o           
          / \          
         /   \         
        /     \        
       /       \       
      /         \      
     o           o     
    / \         / \    
   /   \       /   \   
  o     o     o     o  
 / \   / \   / \   / \ 
o   o o   o o   o o   o

  删除节点的输入格式为：删除第 $i$ 层从左往右数的第 $j$ 个节点。注意删除时，把原有的字符用空格替换，结果是要打印空格的。

分析

  又是一道画图模拟题，需要耐心分析。我采取的是找规律的方法，代码可能长，但是应该比较容易理解吧 $QAQ$ 。

  先看我们得维护什么信息才能实现初始化满二叉树和删点两个操作。初始化的方法有挺多，可以先铺好叶子结点，往上递归建树，也可以从根节点往下建树。但是有个问题是我们并不知道叶子结点到根节点的垂直距离，也不知道根节点的坐标。这时候我们就得找树枝的规律了。建好树后我们要删点，但是输入点的方式不能直接确定点的坐标，得找同一层节点分布的规律。为了后续讨论方便，我们约定叶子节点为第一层，根节点在第 $m$ 层。

树枝的规律

  打表加看图硬分析（这里的树枝长定义为连接第 $i$ 层节点与第 $i+1$ 层节点的树枝长）：

表格如果显示不全可以到我的博客上看

  可以看出，对于第 $i(2 \leq i )$ 层的树枝长，其实是等于前 $i-1$ 层树枝的长度之和与 $i-1$ 的和的。看图更容易发现这一规律：

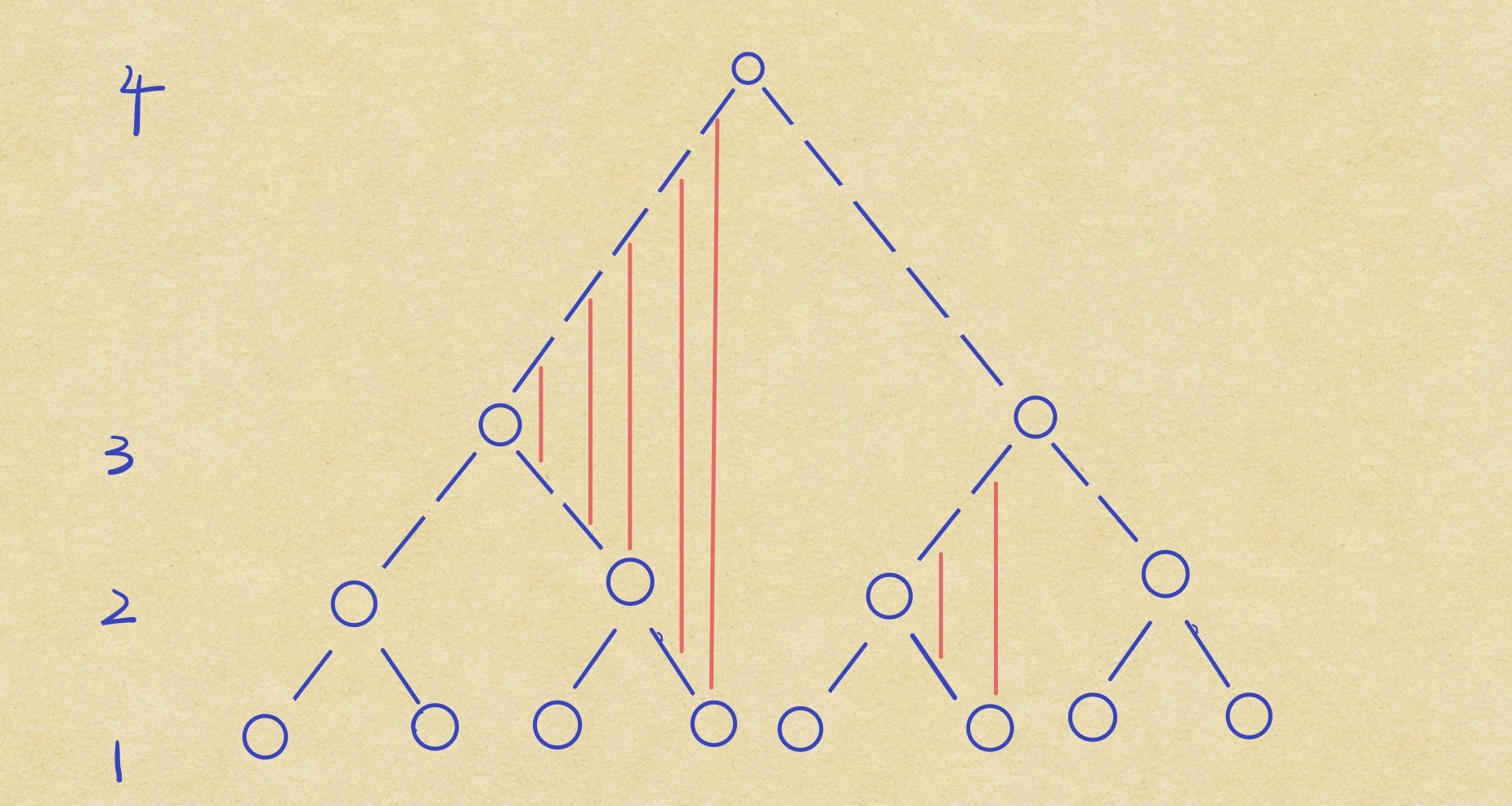
  这里第 $3$ 层的树枝和前两层的树枝和节点有一一对应的关系（红色实线），可以看出长度恰好就是前两层节点数2加上前两层的树枝长度，$O(n)$ 递推可以得到树枝长度数组，记为 $len$ 。

同层节点规律

  观察可知除了第一层外的其他层的同层相邻节点距离是一定的。所以确定每一层第一个节点的位置就可以推出其他节点的位置了。

  让第一层第一个节点水平位置为 $1$ 。再次观察前面的图，可以发现第 $i$ 层第一个节点的水平位置其实就是 $len_i+1$ 。所以根据前面推出来的树枝长数组可以推出。竖直位置就得从根节点（也就是第 $m$ 层）往下推了，根节点竖直位置为 $1$ ，第 $i$ 层竖直位置就其实就是 $=$ 第 $i+1$ 层竖直位置 $+$ 第 $i$ 层的树枝长度 $+1$ ，也是比较明显的。我代码中将两个方向的位置分别用 $pos$ 和 $h$ 表示了。以下是初始化函数和一些数组定义：

const int N = 3100;
int len[20],m,n,pos[20],h[20];
char a[N][N];  //满二叉树数组，注意开大一点
void prepare(){
    int sum = 1;            //记录树枝长的前缀和
    len[1] = 1;pos[1] = 1;  //第一层树枝长为1，第一个节点水平位置为1
    FOR(i,2,m) {
        len[i] = sum + i-1; //递推式子
        sum += len[i];
        pos[i] = len[i] + 1;//顺便得到第i层第一个节点的水平位置
    }
    h[m] = 1;
    for(int i = m-1; i ;i --) h[i] = h[i+1]+len[i]+1;//得到第i层的竖直位置
    memset(a,' ',sizeof(a)); //全都铺满空格
}

  第一层节点的分布已在题目中确定了，相邻节点是兄弟就隔 $3$ 个，不是隔 $1$ 个，因为与其他层分布不同，是要特判的。其他层结点间距也是很好找到规律的，就是 $2 \times len_i+1$ 。至此，我们这棵树的信息基本完备了，下面就是比较轻松的绘制和删点了。

绘制和删点

  这两个操作都是递归进行的。

  因为我们已经知道了每一层的树枝长度，所以我们可以从根节点开始建树，递归左右子树即可。注意我们定义的树枝长度为连接第 $i$ 层节点与第 $i+1$ 层节点的树枝长度。代码采用了前序遍历的方式：

void draw(int x,int y,int depth){
    a[x][y] = 'o'; //画节点
    if(depth == 1) return;  //到叶子节点了，返回
    //开始画树枝，lx,ly定位左树枝，rx,ry定位右树枝
    int lx = x+1,ly = y-1,rx = x+1,ry = y+1;
    FOR(i,1,len[depth-1]){//注意画的树枝长度为下一层的树枝长度
        a[lx][ly] = '/';
        a[rx][ry] = '\\';
        lx = lx+1,ly = ly-1,rx = rx+1,ry = ry+1;
    }
    draw(lx,ly,depth-1);   //画下一层节点
    draw(rx,ry,depth-1);
}

  删点比较暴力，注意删点要同时删除与父亲节点的联系和与孩子节点的联系:

void destroy(int x,int y){
    a[x][y] = ' ';           //将该点置为空格
    if(a[x-1][y-1] == '\\') destroy(x-1,y-1);         //左上角
    if(a[x-1][y+1] == '/')  destroy(x-1,y+1);         //右上角
    if(a[x+1][y-1] == '/' || a[x+1][y-1] == 'o') destroy(x+1,y-1); //左下角，因为往下还要删除孩子节点，要多一个判断
    if(a[x+1][y+1] == '\\'|| a[x+1][y+1] == 'o') destroy(x+1,y+1); //右下角同理
}

一些可能阻止你AC的坑

• 数组大小要开大一点。满二叉树最大层数为 $10$ ，叶子结点的竖直为置最大为 $768$，该层宽度为 $3072$ 。所以数组大小应至少开到 $769*3073$ 。否则可能出现 $\mathbf{Too~ long~ on~ line~ 1}.$ 或者直接 $\mathbf{RE}$ 等错误。
• 数组定义比较多，要用一些比较清晰的变量名，并且时刻记得它们的意义。
• 第 $10$ 个点有点玄学。如果用快读会 $\mathbf{TLE}$ 掉，因为数据量小，全都用 $\mathbf{cin}$ 就可以过了。

$Code:$

#include <bits/stdc++.h>
#define FOR(i,a,b) for(int i = a;i <= b;i++)
using namespace std;
const int N = 3100;
int len[20],m,n,pos[20],h[20];
char a[N][N];  //满二叉树数组，注意开大一点
int read(){int sum = 0,fu = 1;char ch = getchar();while(!isdigit(ch)){if(ch == '-')fu = -1;ch = getchar();}while (isdigit(ch)){sum=(sum<<1)+(sum<<3)+(ch^48);ch = getchar();}return sum*fu;}
//预处理
void prepare(){
    int sum = 1;            //记录树枝长的前缀和
    len[1] = 1;pos[1] = 1;  //第一层树枝长为1，第一个节点水平位置为1
    FOR(i,2,m) {
        len[i] = sum + i-1; //递推式子
        sum += len[i];
        pos[i] = len[i] + 1;//顺便得到第i层第一个节点的水平位置
    }
    h[m] = 1;
    for(int i = m-1; i ;i --) h[i] = h[i+1]+len[i]+1;//得到第i层的竖直位置
    memset(a,' ',sizeof(a)); //全都铺满空格
}

//绘制
void draw(int x,int y,int depth){
    a[x][y] = 'o'; //画节点
    if(depth == 1) return;  //到叶子节点了，返回
    //开始画树枝，lx,ly定位左树枝，rx,ry定位右树枝
    int lx = x+1,ly = y-1,rx = x+1,ry = y+1;
    FOR(i,1,len[depth-1]){ //注意画的树枝长度为下一层的树枝长度
        a[lx][ly] = '/';
        a[rx][ry] = '\\';
        lx = lx+1,ly = ly-1,rx = rx+1,ry = ry+1;
    }
    draw(lx,ly,depth-1);   //画下一层节点
    draw(rx,ry,depth-1);
}

//删点
void destroy(int x,int y){
    a[x][y] = ' ';           //将该点置为空格
    if(a[x-1][y-1] == '\\') destroy(x-1,y-1);         //左上角
    if(a[x-1][y+1] == '/') destroy(x-1,y+1);          //右上角
    if(a[x+1][y-1] == '/' || a[x+1][y-1] == 'o') destroy(x+1,y-1); //左下角，因为往下还要删除孩子节点，要多一个判断
    if(a[x+1][y+1] == '\\'|| a[x+1][y+1] == 'o') destroy(x+1,y+1); //右下角同理
}

//打印
void print(){
    int height = h[1];          //第一层的竖直位置
    int width = 6 * (1<<(m-1)); //第一层的宽度（最宽）
    FOR(i,1,height){
        FOR(j,1,width)
            printf("%c",a[i][j]);
        printf("\n");
    }
}

signed main(){
    m = read();n = read();
    prepare();
    draw(1,pos[m],m); //(1，pos[m])为根节点坐标，位于第m层
    while(n--){
        int i = read(),j = read();
        if(i > 10) continue;
        int x = h[m+1-i],y; //因为层的定义与题目不同，得转化一下
        //分第一层和其他层两种情况计算水平位置y
        if(i == m){
            if(j & 1) y = pos[1] + j/2*6;
            else y = pos[1] + j/2*6 - 2;
        }
        else y = pos[m+1-i] + (j-1)* (2 * len[m+1-i] + 2); //可以手推
        destroy(x,y);
    }
    print();
    return 0;
}

  如果你想练习一下类似的画图题，以下两题可以做做看：

• P1498 南蛮图腾
• P1058 立体图