自动搬运

查看原文

来自洛谷，原作者为

	Twilight_star 生而为赢

搬运于2025-08-24 23:10:45，当前版本为作者最后更新于2025-04-22 19:04:57，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

题目链接

首先先讨论弱化版 P11841 [USACO25FEB] Transforming Pairs S。

弱化版保证 $a,b,c,d>0$。从 $(a,b)$ 开始推有点难，因为很难判断到底要进行多少次各个操作。于是考虑从 $(c,d)$ 开始倒推。

我们发现，$(c,d)$ 的前置状态是确定的：

• 当 $c>d$ 时，只能从 $(c-d,d)$ 转移过来。
• 当 $c<d$ 时，只能从 $(c,d-c)$ 转移过来。
• 当 $c=d$ 时，能从 $(c,0)$ 或 $(0,d)$ 转移过来，但是弱化版讨论范围在正整数，所以暂时不考虑。

这个前置状态很像用更相减损法求 $\gcd$ 的过程。但是更相减损法是 $O(V)$ 的，$V$ 为值域大小。考虑换成更快的欧几里得法求 $\gcd$ 的过程。将多次 $c\gets c-d$ 和多次 $d\gets d-c$ 操作作为一组放在一起讨论。

每一次操作钦定 $c>d$，若不符则 $\operatorname{swap(a,b)},\operatorname{swap(c,d)}$。然后判断是否有 $b=d$ 且 $c$ 减去若干个 $d$ 后能等于 $a$ 即可。时间复杂度为 $O(\log V)$。

---

现在考虑本题。我们按 $a,b,c,d$ 的正负进行分类讨论：

1. $a,b$ 同号 (包含 $a=0$ 或 $b=0$)

此时如果 $a<0$ 或 $b<0$，就把 $a,b,c,d$ 全部变为它自己的相反数。

于是一定有 $a,b\ge 0$。考虑用类似弱化版的做法。但是需要进行更改，因为弱化版不用考虑 $0$ 的情况，本题这里需要考虑。

回顾弱化版，当 $c=d$ 时，会将 $c$ 或 $d$ 减为 $0$。换成欧几里得法，就是 $c \bmod d=0$ 时，会将 $c,d$ 其中一个减为 $0$。则进行分类讨论：

• 如果将 $c$ 减为 $0$

  则最终 $(c,d)$ 会成为 $(0,d)$。于是 $a=0$ 且 $b=d$ 则可以成功。

• 如果将 $d$ 减为 $0$

  则一定是将 $(c,d)$ 减为 $(d,d)$ 然后再一步减为 $(d,0)$。所以 $a=d$ 且 $b=0$ 时也是可以的。

代码如下：

int calc(int a,int b,int c,int d)
{//计算 a,b>=0 时的答案
	if(c<0||d<0) return -1;
	if(a==c&&b==d) return 0;
	int res=0;
	while(c!=0&&d!=0)
	{
		if(a==c&&b==d) return res;
		if(c<d) swap(c,d),swap(a,b);
		if(b==d&&c>=a&&c%d==a%d) return res+(c-a)/d;//能否把c删成a 
		if(c%d==0&&((a==0&&b==d)||(a==d&&b==0))) return res+c/d;//删成0是否满足要求 
		res+=c/d;
		c%=d;
	}
	if(a==c&&b==d) return res;
	return -1;
}
void solve()
{
	a=read(),b=read(),c=read(),d=read();
	if(a==c&&b==d) return printf("0\n"),void();
	if(a<=0&&b<=0) a=-a,b=-b,c=-c,d=-d;
	if(a<0) swap(a,b),swap(c,d); 
	if(a>=0&&b>=0)//a,b同号 
	{
		if(c<0||d<0) return printf("-1\n"),void();
		return printf("%lld\n",calc(a,b,c,d)),void();	
	}
}

2. $a,b$ 异号，$c,d$ 异号

我们会发现，在操作途中，当 $a,b$ 从异号变成了同号，则不可能再变成异号。

于是当 $a,c$ 不同号，$b,d$ 不同号时则无解。

剩下的情况仅剩 $a,c$ 同号，$b,d$ 同号。我们模拟从 $(a,b)$ 出发的操作，因为不能让数改变符号，所以每一次只能是让绝对值大的数加上绝对值小的数。并且操作途中 $a,b$ 的绝对值会不断减小。

举个例子，现在 $(a,b)$ 满足 $|a|>|b|,a>0,b<0$，此时则一定变成 $(a+b,b)$，则只看绝对值的话会从 $(|a|,|b|)\to (|a|-|b|,|b|)$。这样只看绝对值是不是有点像上种情况的从 $c,d$ 倒推的情形。

于是这种情况的答案为上种情况 $(c,-d)\to (a,-b)$ 的答案。（钦定 $c>0$）

//a,b异号，c,d异号，已保证a>0
if(c<0&&d>0) return printf("-1\n"),void();
if(c>=0&&d<=0) return printf("%lld\n",calc(c,-d,a,-b)),void();

3. $a,b$ 异号，$c,d$ 同号

现在需要考虑 $a,b$ 从异号变为同号的过程。先钦定 $a,c,d>0,b<0$。如果不符可以通过交换和取相反数满足。

我们把它搬到平面直角坐标系上讨论。存在两个坐标 $(a,b),(c,d)$。那么无论是从 $(a,b)$ 开始推还是从 $(c,d)$ 开始倒推都是不断在向 $x$ 轴靠近。直到某一次操作我们让 $(a,b)$ 变为同号。

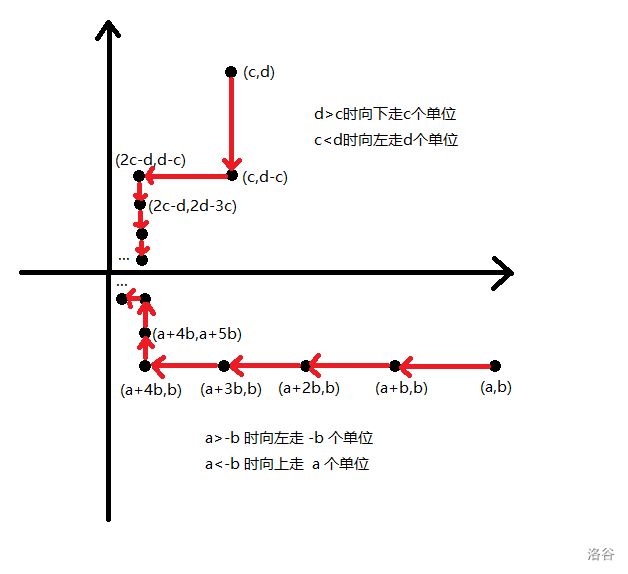
其实什么时候让 $a,b$ 变为同号是我们自己选择的。当 $a>-b$ 时，如果不想跨过 $x$ 轴则走到 $(a+b,b)$，但是如果我们向跨过 $x$ 轴，则可以直接走到 $(a,a+b)$。

如下图，蓝色边为跨过 $x$ 轴的转移边。

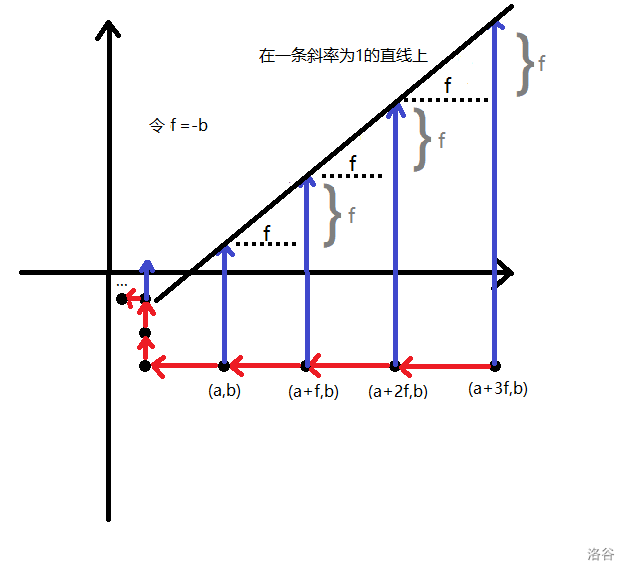
我们会发现，对于一段连续的向左的一组转移，我们可以从中选择一个点向上转移，并且向上转移后的落点在一条斜率为 $1$ 的直线上。

但是，有些落点是无法到达 $(c,d)$ 的。所以我们还要求出可以到达 $(c,d)$ 的所有点，再与所有落点取交集，才是真正合法的落点。

设 $(x,y)$ 为真正合法的落点之一，根据落点的定义，则一定有 $x<y$。所以从 $(c,d)$ 开始倒推的话， 到达 $(x,y)$ 下一步应该向左走。于是将所有向左走的点与所有落点取交即可。

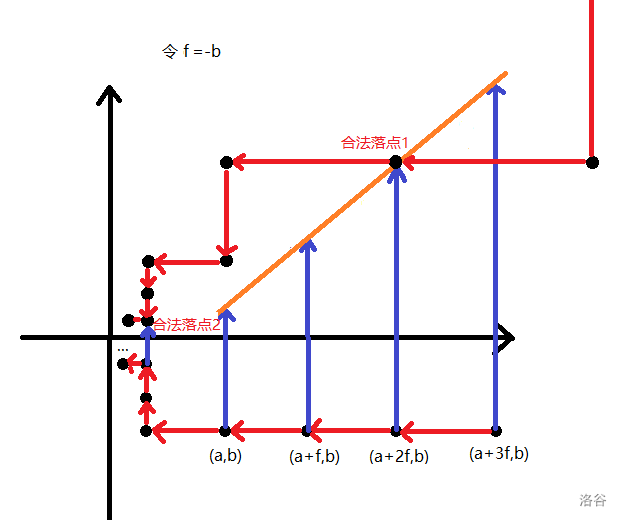
于是枚举 $(c,d)$ 倒推向左走的每一组，并预处理出 $(c,d)$ 到这一组第一个点的操作次数。再枚举 $(a,b)$ 正推向左走的每一组，并预处理出 $(a,b)$ 到这一组第一个点的操作次数。

然后对交点计算总的操作次数即可。

注意不要漏掉落点在 $x$ 轴上的情况。

总时间复杂度 $O(q\log^2V)$。

具体判断条件见代码：

//a,b异号，c,d同号
if(c<=0&&d<=0) a=-a,b=-b,c=-c,d=-d; 
if(a<0) swap(a,b),swap(c,d);

vector< array<int,3> > q;
for(int x=c,y=d,num=0;x>0&&y>0;)
{
  if(y>=x) num+=y/x,y%=x;
  else q.push_back({y,x,num}),num+=x/y,x%=y;
}//预处理 (c,d) 倒推时到达每一个向左组的操作次数 

int ans=inf,num=0;//num为(a,b)到当前组的 
while(a>0&&b<0)
{
  if(a+b==0)//向上走到坐标轴上 
  {
    ans=min(ans,num+1+calc2(a,0,c,d)); //calc2(a,b,c,d): 当calc(a,b,c,d)==-1时为inf，否则为calc(a,b,c,d) 
    break;
  }
  if(a+b<0)//向上走，不用考虑穿过坐标轴 
  {
    num+=(-b)/a;
    b=-((-b)%a);
    continue;
  }
  //向左走 
  for(auto i:q)//枚举 (c,d) 倒推途中向左转移的组 
  { 
    int y=i[0],mx=i[1];
    if(y<=a+b&&(a-y)%(-b)==0)//(a,a+b)为本组最右的落点 
    {
      int k=(a+b-y)/(-b);//本组第几个点 
      int x=a+k*b;//落点横坐标 
      if(x<=mx&&(mx-x)%y==0) ans=min(ans,num+i[2]+1+k+(mx-x)/y);//落点能在(c,d)路径上 
    }
   } 
  if(a%(-b)==0) ans=min(ans,num+a/(-b)+calc2(-b,0,c,d));//向上拐，走到x轴上 
  num+=a/(-b);
  a%=(-b);
}
if(a>=0&&b>=0) ans=min(ans,num+calc2(a,b,c,d));
if(ans>=inf) printf("-1\n");
else write(ans),putchar('\n');