自动搬运

查看原文

来自洛谷，原作者为

	CarroT1212 chrono::system_clock::now().time_since_epoch().count()

搬运于2025-08-24 23:10:36，当前版本为作者最后更新于2025-03-03 12:48:56，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

25-8-6 upd：修改了一些比较奇怪的措辞。

提供一个不涉及太多图论知识的强行讨论做法。

首先定好转化方向：有一个图 $G$，要将它的点按某种顺序排成一行，连接这些点的边呈一个括号匹配状态（即如果把这些边放到这一行点的同一侧画出来，可以没有边在非端点处相交）。比如这样。

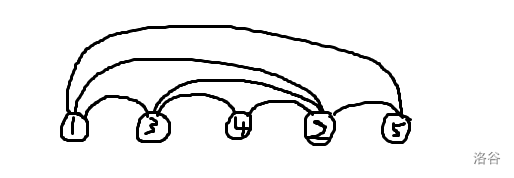
然后我们希望这个重排方案满足：对于重排后的第一个位置，它在原图中对应的点的编号尽量小，如果两种方案相同就比较第二个位置……那么可以这样理解字典序最小的限制：有一个答案序列，我们每次需要在保证有解的情况下，把编号最小的一个点加到答案序列后面。

以下如果无特殊说明，称“位置”为答案序列里的位置（重排后的编号），“点”为原图的点。

AC 性质（树）

省流：从 $1$ 开始递归，每次把当前点自己和儿子的子树最小值搓到一起排序，从小到大遍历，如果是儿子就进入儿子子树递归，如果是自己就把自己加到答案序列后面。

显然任何树都是有解的，只要把原图的点按任意 dfn 重排即可。但这样未必最优。

首先把 $1$ 作根并且直接将 $1$ 推进答案。然后考虑它的后代被推进答案的顺序有什么限制。

观察：$1$ 的每棵子树分配到的位置都必须是一段连续区间。不然如果有不同子树混在一起，那么各个子树里连接的边排开来一定会相交。所以不同子树就独立开了。

考虑按什么顺序把连续区间分配给这些子树。画一下可以得知：每棵子树里的任何一个点，作为子树中第一个被推进答案的点，都有解。也就是如果我们即将处理一棵 $1$ 的子树，那么紧接着第一个被推进答案序列的点，一定可以是这个子树里的最小值。

所以应该按子树内最小值从小到大处理 $1$ 的儿子子树，递归地处理即可。考虑进入儿子子树后该如何确定顺序。设这个儿子为 $p$。$p$ 的每棵子树分配到的位置也必须是连续区间。

和 $1$ 的情况不同的地方在于，$p$ 不一定是子树内最小值，所以它并不一定是第一个被推进答案的点。这个问题其实很好解决：我们把 $p$ 自己也和 $p$ 的每棵儿子子树（的最小值）放到一起进行排序。在按顺序进儿子子树的过程中如果遇到的是 $p$ 就把 $p$ 自己推进答案即可。$1$ 的情况也可以这么写。

于是这样递归下去就行了，没有实现难度。至此 $32$ 分。画个比较扭曲的例子。

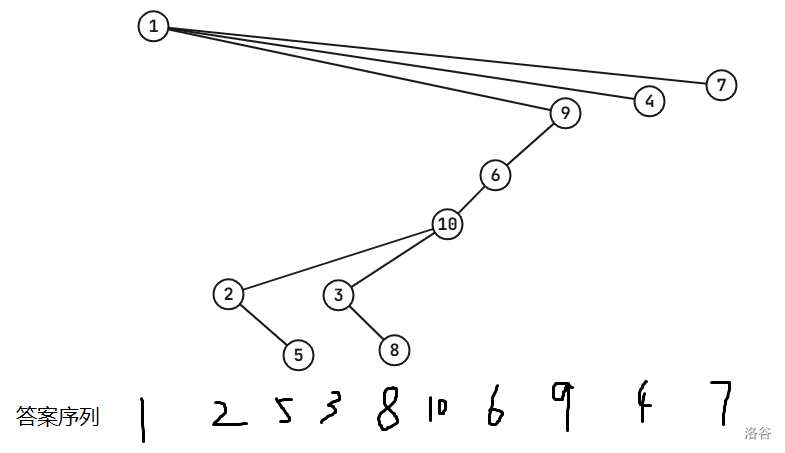
我现场的想法比这要复杂一些，就是每次我需要把子树内最小值到根的这条链拿出来，依次处理上面挂的子树。其实本质完全是一样的，不过后面推广就需要多转几个弯了。

C 性质（森林）

实际上和树没什么差别。思考可以得知，不同的树占用的位置区间（即能包含一棵树在答案序列里的所有位置的极小区间），只可能包含或不交。也就是我们一旦开始做一棵树，就要把它做完，或者在里面开始一些新的树。否则必定不合法。

那么稍微修改一下树的做法就好了：每次我们想把一棵树的一个点推进答案的时候，如果存在比它更小的点，所在的树还没有被处理过，我们就先以这个更小的点为根进入它所在的树进行处理，完全处理完再回来继续做原本这棵树的情况。（注意这样的未被处理的更优点可能有很多个）

容易实现。至此 $52$ 分。

实际上，树 $\to$ 森林的方法，在连通块 $\to$ 任意图上也是成立的。所以目标就是把连通块的做法搞出来。

A 性质（连通块）

也许无关紧要地证明一个事情：第一个位置还一定可以是 $1$。可以看看上面的第一张图，显然把答案序列的一段前缀反过来拼到后面并不会导致原本不相交的边相交，那对于一个合法的答案序列我们一定可以把 $1$ 调整到最前面。然后考虑怎么做。

（赛时止步于此，感谢 @Nightingale_OI 和 @hxhhxh 对思路的指教）

比较对我电波的一种做法是，尝试把图刻画为 dfs 树+若干返祖边。所以现在要考虑的只是树的情况上面多了返祖边应该怎么办。

由于题目保证有解，所以其实这里很多图形态都是不需要考虑的，这个得等具体分析的时候去看。

直接套树的做法的问题是，“子树里每个点都可以第一个被推进答案”的结论不成立了，可能会触发某些返祖边的限制。我们希望知道，现在该如何找出每个子树里可以第一个推进答案的点。

比如给刚刚图里的那棵树加上几条返祖边，它的最优方案会变成这样：

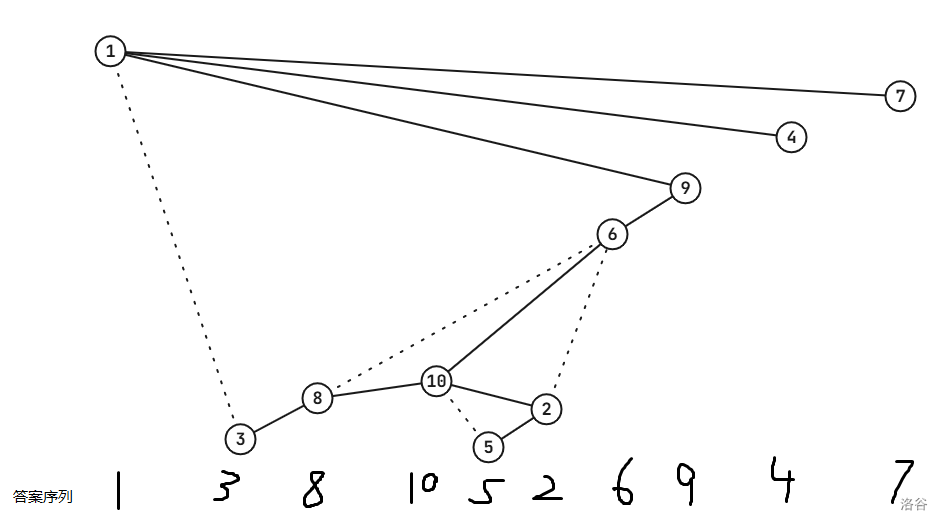
（其实画岔了，并不是同一棵树，但是意思到了就行）

考虑 $3\to 1$ 那条返祖边。它本质上限制了：$3\rightsquigarrow 6$ 这一整条链（$6$ 的意义是 $1$ 在 $3$ 方向上的二级儿子），它们都需要同时成为父亲的第一个被处理的儿子，或者同时成为最后一个被处理的。只有这样才能让 $3\to 1$ 不和 $3\rightsquigarrow 1$ 上的任何东西相交。

这里同时成为第一个儿子是更优的，可以先把 $3$ 推进答案。而 $2$ 就推不进去，因为总会因为返祖边限制导致不得不有更大的点挡在前面。

结合这个例子，我们可以得到答案处理顺序符合返祖边限制的一个必要条件：一个点 $p$，如果某些儿子子树里有返祖边连向了 $p$ 的祖先，那么这样的儿子子树一定要被放在 $p$ 的儿子（和 $p$ 自己）中第一个处理，或者最后一个处理。显然这样的子树每个点最多只有两棵（如果有两棵就是一个最前一个最后）。

以及，因为一些这样的特殊子树可能是因为同一条返祖边产生的，所以还有一个必要条件就是同步限制：如果一个点的特殊子树被放在第一个（最后一个）处理，那么它的父亲的因同一条返祖边产生的特殊子树也要放在第一个（最后一个）处理。有些点可能没有这个限制。

显然，同时满足两个必要条件就是答案序列合法的充要条件。强烈建议手画感受一下。

每个 $p$ 上具体的限制容易类 tarjan 地预处理。称这至多两个被限制的儿子为限儿，子树内可能被第一个推进答案的点叫做打头点。（奇怪的命名。）

分别维护每个 $p$：无限儿时子树内最小的打头点；有一个限儿时，限儿被第一个处理和最后一个处理时，最小的打头点；有两个限儿时，它们在处理顺序上分别被排在头尾和尾头时，最小的打头点。

一遍树形 DP 就可以转移这几个东西。整体思路是，对于没被限住的子树还是取最优打头点贪心排序；限儿就分讨一下放在最前面还是最后面，并分别处理，在保证父子限制同步的情况下，有哪些状态可能转移上来。

这里详细列一下父子限制同步的所有可能情况。

假设我们现在让 $p$ 的某个限儿 $u$ 被第一个处理，找 $u$ 能转移到 $p$ 的方案都有什么。手画一下可以发现，只有如下的四种情况。

图丑见谅。其中 $v,w$ 都指 $u$ 的限儿。

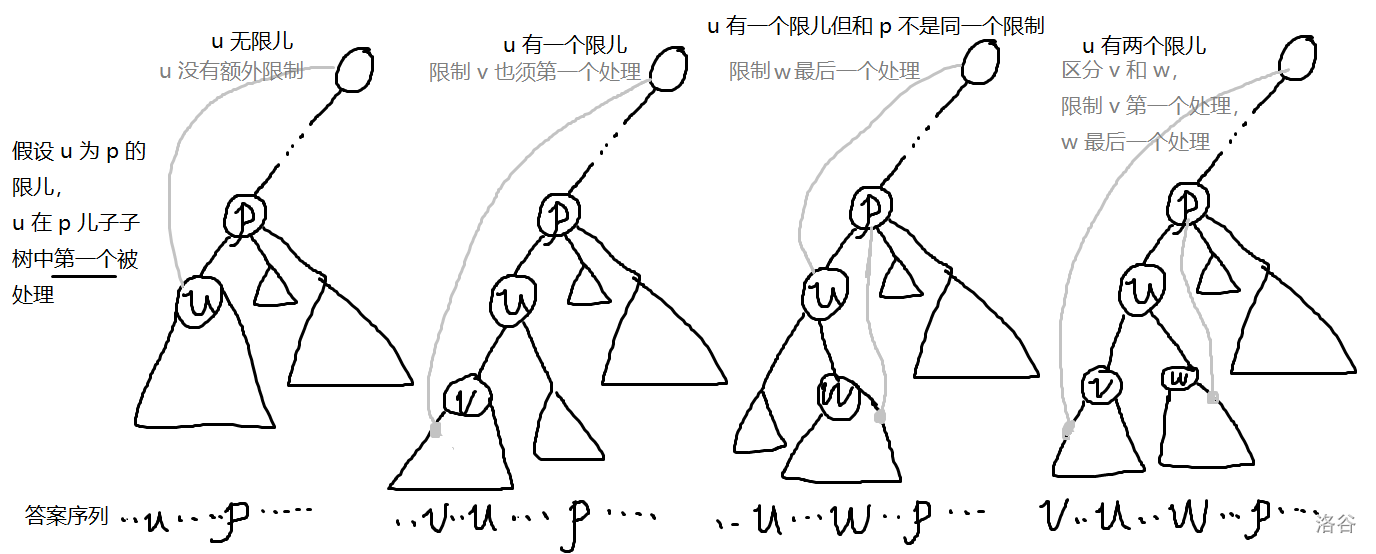
注意后两种情况，$w$ 只能是接在 $p$ 上的，不然就无解了。

$u$ 被最后一个处理的情形和上面是恰好相反的，不再赘述。

剩下的非限儿用 DP 出的最小打头点从小到大排好。完成 DP 后按照最优值对应的顺序生成答案序列即可。

@beta99999 在评论中提出的做法：对「限儿」建立二叉树，tarjan 找到割点的时候中序遍历，遍历每个节点前根据 low 与当前节点的一致性决定是否交换左右儿子。遍历的结果就是点双的哈密顿回路。

实现细节较多，至此 $72$ 分。

正解（一般图）

已经结束咧！用森林一样的方法套连通块情况即可。至此 $100$ 分。线性或带 $\log$ 都可通过。

#include <bits/stdc++.h>
#define pb push_back
#define fi first
#define se second
using namespace std; bool MEM;
using ll=long long; using ld=long double;
using pii=pair<int,int>; using pll=pair<ll,ll>;
const int I=1e9,N=2e5+7;
const ll J=1e18;
int type,n,m;
int vis[N],dfn[N],cnn,low[N],st[N][2],tp[N],dp[N][2];
vector<int> e[N],ans;
vector<pii> e1[N],to[N][2];
set<int> s;
void joi(vector<pii> &x,vector<pii> &y) { for (pii i:y) x.pb(i); }
int cal(int x,int p) {
	if (!tp[x]) return dp[x][0]>dp[x][1];
	else if (tp[x]==1) return low[st[x][0]]==dfn[p]; 
	else { int xx=low[st[x][0]],yy=low[st[x][1]]; return xx==yy?dp[x][0]>=dp[x][1]:xx>yy; }
}
void dfs(int p,int f) {
	dfn[p]=low[p]=++cnn,dp[p][0]=dp[p][1]=p;
	for (int i:e[p]) if (i!=f) {
		if (!dfn[i]) {
			dfs(i,p),low[p]=min(low[p],low[i]);
			if (low[i]<dfn[p]) st[p][tp[p]++]=i;
			else e1[p].pb({i,dp[i][0]>=dp[i][1]});
		}
		else low[p]=min(low[p],dfn[i]);
	}
	e1[p].pb({p,0});
	sort(e1[p].begin(),e1[p].end(),[&](pii x,pii y){return dp[x.fi][x.se]<dp[y.fi][y.se];});
	int x=st[p][0],y=st[p][1];
	if (tp[p]>=1) to[p][0].pb({x,cal(x,p)});
	if (tp[p]>=2) to[p][1].pb({y,cal(y,p)});
	for (pii i:e1[p]) to[p][0].pb(i),to[p][1].pb(i);
	if (tp[p]>=1) to[p][1].pb({x,cal(x,p)^1});
	if (tp[p]>=2) to[p][0].pb({y,cal(y,p)^1});
	pii xx=to[p][0][0],yy=to[p][1][0];
	int wx=dp[xx.fi][xx.se],wy=dp[yy.fi][yy.se];
	dp[p][0]=wx,dp[p][1]=wy;
}
void dfs2(int p) { s.erase(p),vis[p]=1; for (int i:e[p]) if (!vis[i]) dfs2(i); }
void dfs1(int p,int x) {
	if (s.count(p)) dfs2(p),x=dp[p][0]>=dp[p][1];
	for (pii i:to[p][x]) {
		if (i.fi==p) {
			while (s.size()&&*s.begin()<p) dfs(*s.begin(),0),dfs1(*s.begin(),0);
			ans.pb(p);
		}
		else dfs1(i.fi,i.se);
	}
}
void mian() {
	scanf("%d%d",&n,&m),ans.clear(),cnn=0;
	for (int i=1;i<=n;i++)
		e[i].clear(),e1[i].clear(),to[i][0].clear(),to[i][1].clear(),vis[i]=dfn[i]=tp[i]=0,
		s.insert(i);
	for (int i=1,x,y;i<=m;i++) scanf("%d%d",&x,&y),e[x].pb(y),e[y].pb(x);
	for (int i=1;i<=n;i++) if (!dfn[i]) dfs(i,0),dfs1(i,0);
	for (int i:ans) cout<<i<<" \n"[i==ans.back()];
}
bool ORY; int main() {
	// while (1)
	int t; for (scanf("%d%d",&type,&t);t--;)
	mian();
	cerr<<"\n"<<abs(&MEM-&ORY)/1048576<<"MB";
	return 0;
}