自动搬运

查看原文

来自洛谷，原作者为

	Md_Drew 仰天大笑出门去

搬运于2025-08-24 21:22:11，当前版本为作者最后更新于2019-01-27 18:42:38，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

超详解释 虽然我没学过向量

其实本题还算简单， 要是任意的多边形模拟就会爆炸了。下面实在不能理解的就当公式感性理解一下吧

---

---

矢量的概念：

如果一条线段的端点是有次序之分的，我们把这种线段成为有向线段(directed segment)。

如果有向线段p1，p2的起点p1在坐标原点，我们可以把它称为**矢量(vector) **p2。

---

矢量矢量加减法：

设二维矢量P = ( x1, y1 )，Q = ( x2 , y2 )。

则矢量加法定义为： P + Q = ( x1 + x2 , y1 + y2 )，同样的，矢量减法定义为： P - Q = ( x1 - x2 , y1 - y2 )。

---

矢量的点乘：

P=(x1, y1)，Q=(x2, y2)。则

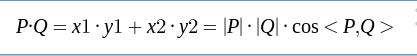
点乘法可以看成一个向量在另一个向量上的投影与另一个向量的模长相乘。

---

向量的叉乘

设矢量P = ( x1, y1 )，Q = ( x2, y2 )

则矢量叉积定义为由(0,0)、p1、p2和 p1+p2 所组成的平行四边形的带符号的面积。

感兴趣的可以去百度一下右手定则

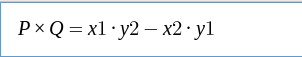
其结果是一个标量。

其绝对值等于

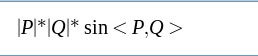
使用向量的叉乘可以判断向量的方向。

若 P × Q > 0 , 则P在Q的顺时针方向。

若 P × Q < 0 , 则P在Q的逆时针方向。

若 P × Q = 0 , 则P与Q共线，但可能同向也可能反向。

实际上在OI中，叉乘用的多。其他的都跟狗屎一样

---

进入正题

好吧我个蒟蒻前面的定义全是从学长ppt拿来的真的不好说什么了

下面来举个例子

比如这张图

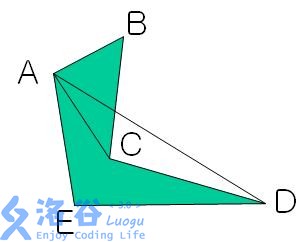
我们随便取一个点D作为我们的基准点。连接BD， DA。

通过**1/2（DE叉乘AD + DA叉乘DB + DB叉乘DC **

(注意严格按照点的逆时针方向来算，不然你怎么都推不出面积)

之前我就是因为这样跟个SB一样的推了半天

那么运用我们之前所学的知识，也知道整个图形面积等于

三角形DEA + 三角形 DAB + 三角形 DBC

那你就会问了，这面积难道不重叠了吗？？

注意，用叉乘算的三角形DEA + 三角形 DAB的值是负的， 而叉乘算的三角形 DBC的值是正的，等价于去掉了重叠部分。

但是也要注意，最后的结果是负的

同理，如果我们以C为基准点的话，那么面积为

三角形CED + 三角形CAE +三角形CAB

---

如果懂的话可以自己推导一下，下面的图形面积

注意下面的是以原点为基准，那么就意味着我们要算n次，而不是之前推的n-2次

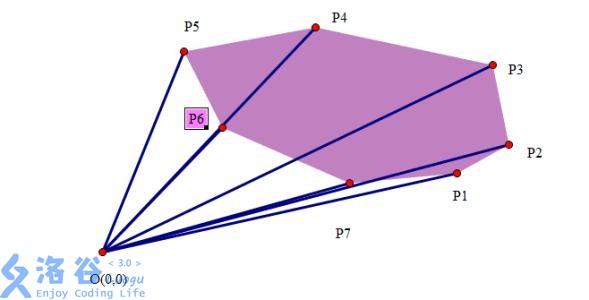
意会一下吧!映像会更深刻

---

下面我就发放代码了。

#include<cstdio>
#include<cmath>
using namespace std;
int n;
int x[110], y[110];
int ans;


int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;++i)	scanf("%d%d",&x[i],&y[i]);

	x[n+1] = x[1], y[n+1] = y[1];//注意算n次会涉及到n+1的点，那么这个点即是第一个点

	for(int i=1;i<=n;++i)   ans += (x[i]*y[i+1] - x[i+1]*y[i]);

	printf("%d",abs(ans/2) );//我们最后再取绝对值除二
	return 0;
}