自动搬运

查看原文

来自洛谷，原作者为

	wuenzi **

搬运于2025-08-24 23:09:46，当前版本为作者最后更新于2025-02-13 10:24:08，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

建树

我们可以将过程转化成一棵三叉树。

我们对样例进行建树（自下而上）。

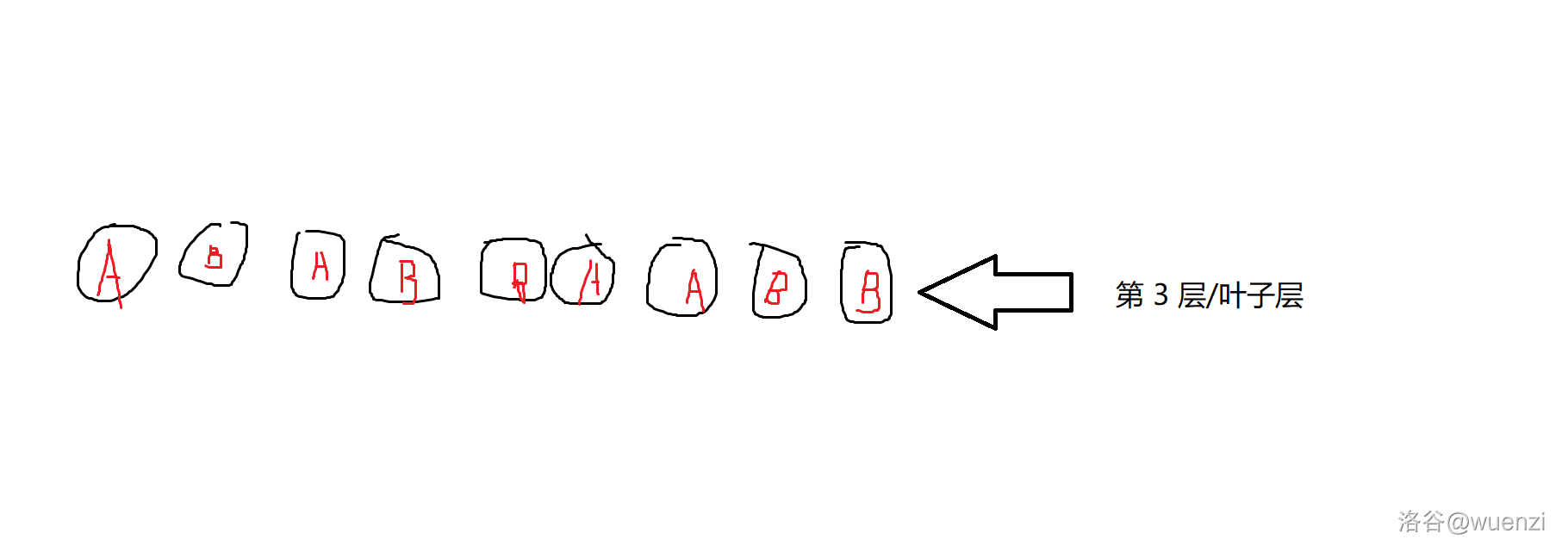
让后建第二层。

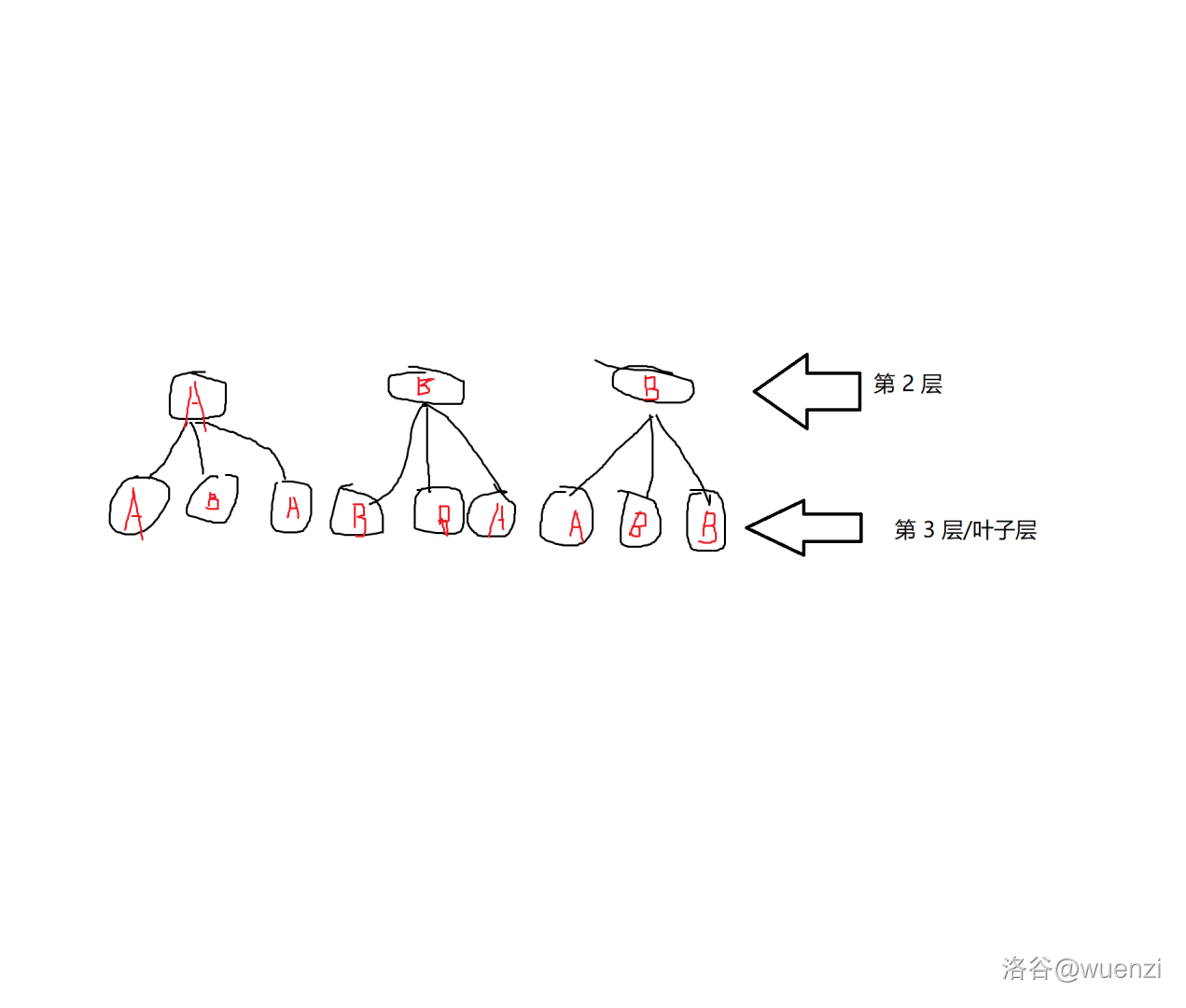
最后确定根。

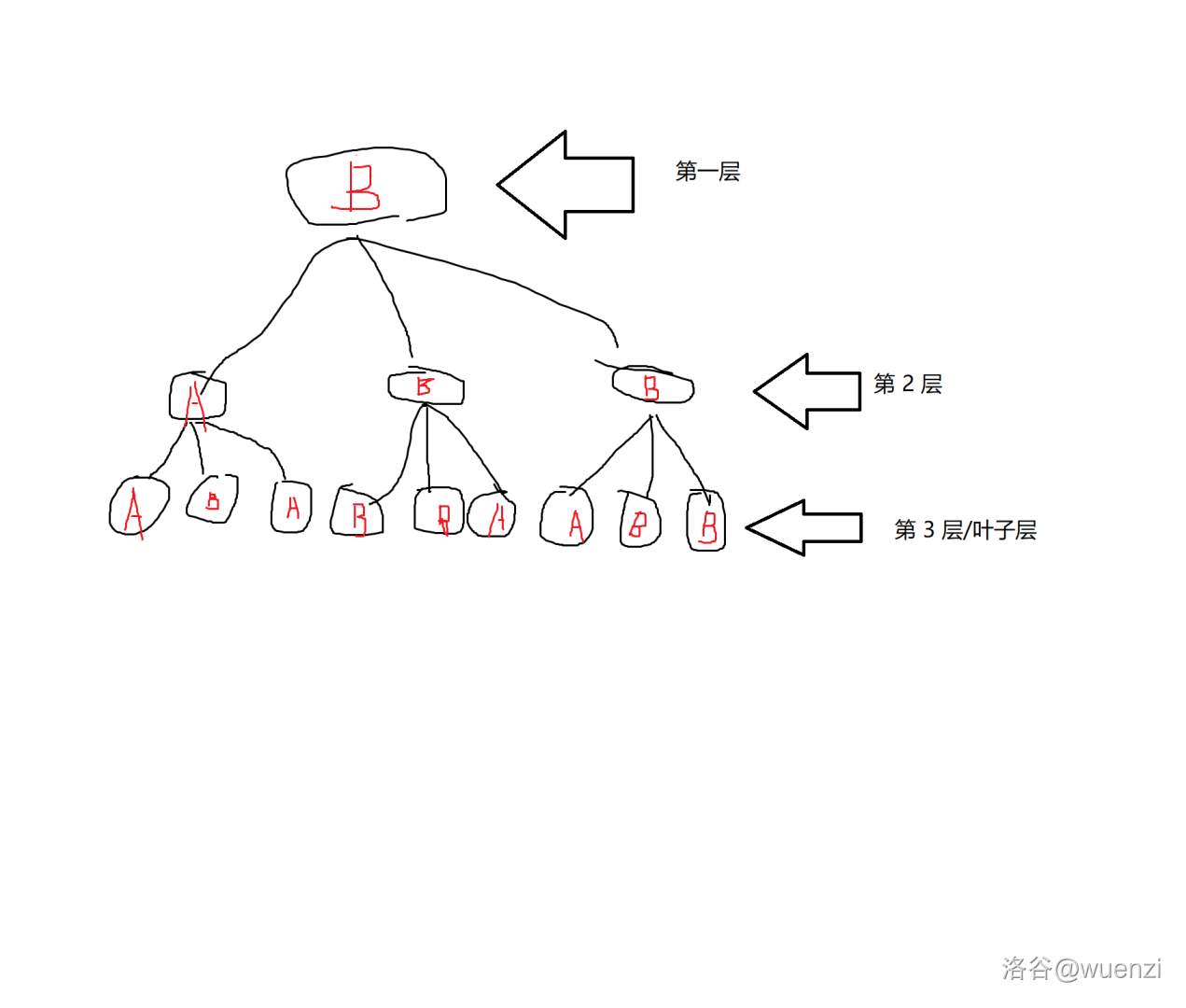
我们易知不进行任何事件时的答案为根。

我们就可以写出建树。

char build(int u,int d){
	if(d==n){
		w[cnt]=u;//第 cnt 个人的选择在树中的下标
		return a[u].v=l[cnt++];
	}
	a[u].l=3*u;//左
	a[u].mid=3*u+1;//中
	a[u].r=3*u+2;//右
	map<char,int> v;
	v.clear();
	v[build(3*u,d+1)]++;
	v[build(3*u+1,d+1)]++;
	v[build(3*u+2,d+1)]++;
	if(v['A']>v['B'])return a[u].v='A';
	else return a[u].v='B';
}

修改

利用上面的 $w$ 数组，我们可以直接修改树中结点。

我们先来计算一下样例 $1$ 中的第 $3$ 个询问。 所以我们直接修改这个节点以及这个节点的所有祖先即可。

最后答案仍然是根节点。

修改的代码如下。

char qz(int u){
	map<char,int> v;
	v.clear();
	v[a[3*u].v]++;
	v[a[3*u+1].v]++;
	v[a[3*u+2].v]++;
	if(v['A']>v['B']){
		a[u].v='A';
	}else{
		a[u].v='B';
	}
	if(u==1)return a[u].v;//如果为根，直接返回
	return qz(u/3);
}

完整代码

#include<bits/stdc++.h>
#define int long long
#pragma GCC optsize(2)
using namespace std;
int n,Q;
string l;
struct WZOI{
	int l,mid,r;
	char v;
}a[10000005];
int cnt=1;
int w[10000005];
char build(int u,int d){
	if(d==n){
		w[cnt]=u;
		return a[u].v=l[cnt++];
	}
	a[u].l=3*u;
	a[u].mid=3*u+1;
	a[u].r=3*u+2;
	map<char,int> v;
	v.clear();
	v[build(3*u,d+1)]++;
	v[build(3*u+1,d+1)]++;
	v[build(3*u+2,d+1)]++;
	if(v['A']>v['B'])return a[u].v='A';
	else return a[u].v='B';
}
char qz(int u){
	map<char,int> v;
	v.clear();
	v[a[3*u].v]++;
	v[a[3*u+1].v]++;
	v[a[3*u+2].v]++;
	if(v['A']>v['B']){
		a[u].v='A';
	}else{
		a[u].v='B';
	}
	if(u==1)return a[u].v;
	return qz(u/3);
}
signed main(){
	cin>>n>>Q>>l;
	int n3=l.size();
	l=' '+l;
	build(1,0);
	while(Q--){
		int x;
		cin>>x;
		a[w[x]].v=(a[w[x]].v=='A'?'B':'A');
		cout<<qz(w[x]/3)<<endl;
	}
	return 0;
}

时间复杂度

首先是建树，每个节点遍历 $1$ 次，一共 $3^N$ 个节点，建树复杂度 $\Theta(3^N)$。

然后是修改，修改一共遍历 $N$ 个节点，一共修改 $Q$ 次，修改复杂度 $\Theta(N \times Q)$

所以总复杂度 $\Theta(3 ^ N + N \times Q)$